Regular Expressions
正则表达式
Regular Expressions
在文本中查找子字符串只是寻找一个单一的字符串,但经常的我们可能不知道这个字符串的完整信息,或是寻找的是吻合某种模式的一些字符串,即所谓 模式匹配(Pattern Matching)。
正则表达式(Regular Expressions) 就是用来描述模式的,表示符合某种模式的字符串的集合(可能是无限的),它有下面几种基本操作:
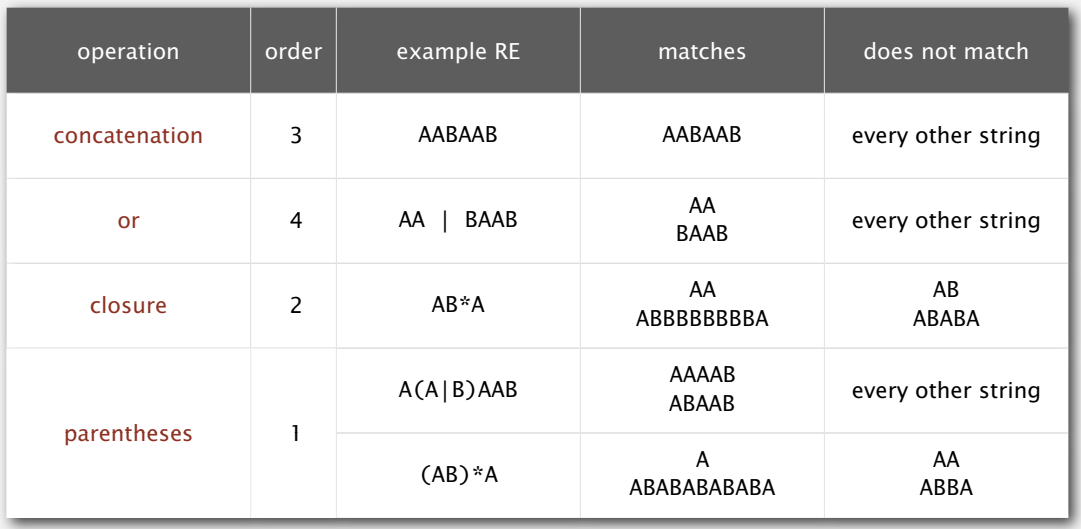
连接、或、闭包和括号,都不难理解。其中闭包表示若干个自身连接,可以是零个。
为了便于表示实际的模式,一般还会有些额外的缩略写法:
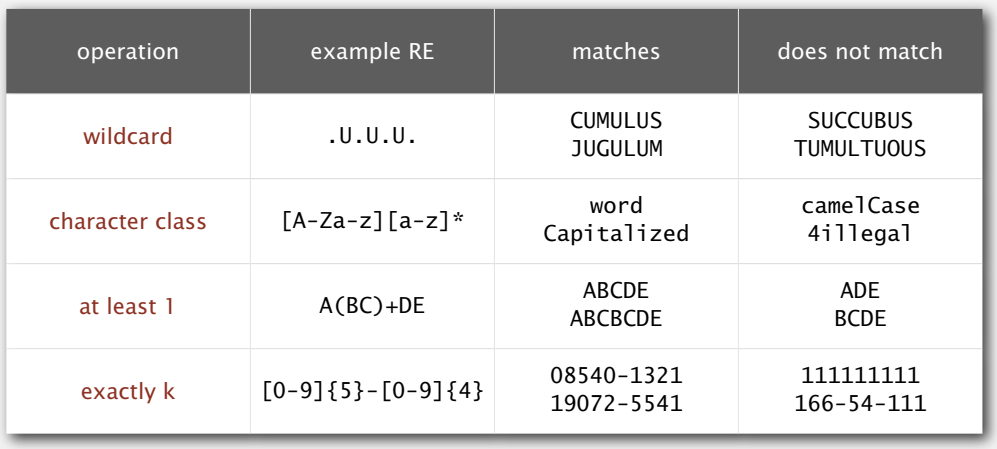
通配符(.)可以表示任意字符,包含在方括号中的一系列字符(- 可表示范围)表示这些字符中的任意一个,加号表示至少连接一次的特殊闭包,花括号可以指定次数(也可以用 - 指定允许的次数范围)。还有问号表示连接一次或零次的闭包,^ 表示补集,构造正则的元字符可以加上反斜杠来转义等等。
正则表达式很强大,可以描述很多模式,但不易读,也就不容易调试,要小心使用。而且,也具有一定的局限性,像没法描述 A 和 B 数量一样的字符串。
REs And NFAs
其实,正则表达式和确定型有穷自动机间存在着二元性(duality),即 Kleene 定理所说:对任意 DFA 存在着描述同样字符串集合的正则表达式,对任意正则表达式存在着识别同样字符串集合的 DFA。例子:
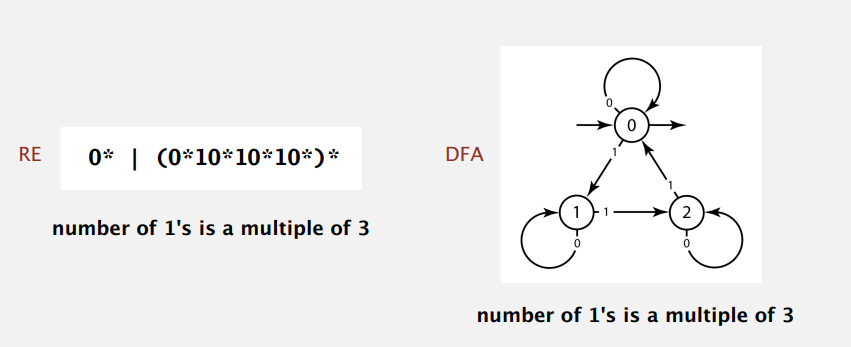
实现模式匹配的第一次尝试是模仿 KMP 算法,从正则表达式构造 DFA,用输入文本来转移状态,能到终结状态就表示匹配成功。同样的,好处是在输入流中没有回退,也有线性时间的性能保证。但是,这方法并不可行,因为正则表达式对应的 DFA 的状态数目可能是指数级的。
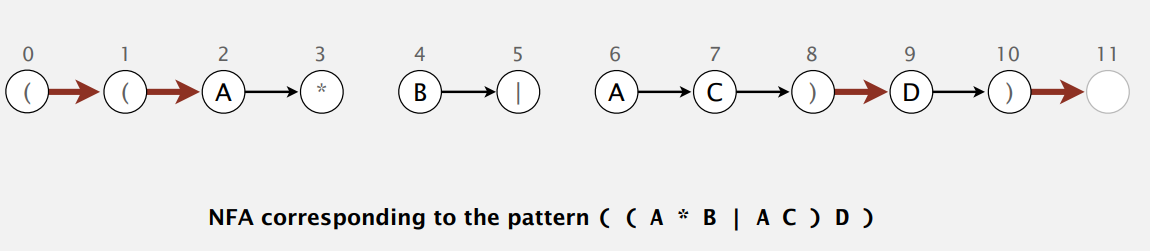
于是乎,我们来了解下非确定型有限状态自动机(Nondeterministic finite state automata,NFA),状态间的转移是不确定的。正则表达式匹配的 NFA:
- 正则表达式用括号括起。
- 正则每个符号对应 NFA 一个状态,再加个接受状态。
- 接受空串 \(\epsilon\),不扫描下个字符而直接改变状态(下图红线),不确定性所在。
- 扫描字符,匹配转移到一下个状态(下图黑线)。
- 在扫描完全部文本字符后,如果有 任一 转移序列到达接受状态,则匹配成功。
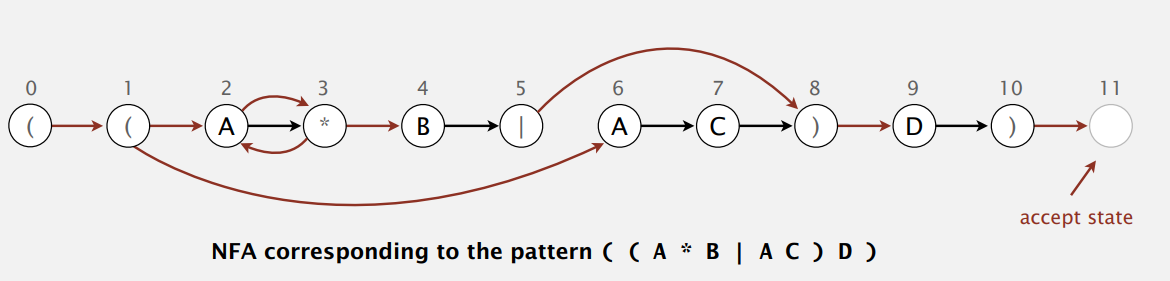
因为 NFA 接受空串,不扫描字符也能改变状态,所以同一输入在 NFA 会有很多条路可走。只要有一条走到了接受状态,那就匹配成功。如果不匹配的话,那也要走完所有可能的路。所以,下面我们要解决如何系统地考虑所有可能的转移序列。
NFA-simulation
首先我们这样来表示 NFA:用整数 0 到 M(正则长度)来标号状态(像上图),用数组 re 来存储正则表达式,用有向图来存储空转移(\(\epsilon-transitions\),上图红线)。
至于怎么模拟 NFA 输入文本运行,感觉类似广搜,维护每一步所有可能走到的状态,下一步再拓展这些状态,要是文本流结束那步的状态里包含接受状态,就表示匹配成功。例图:
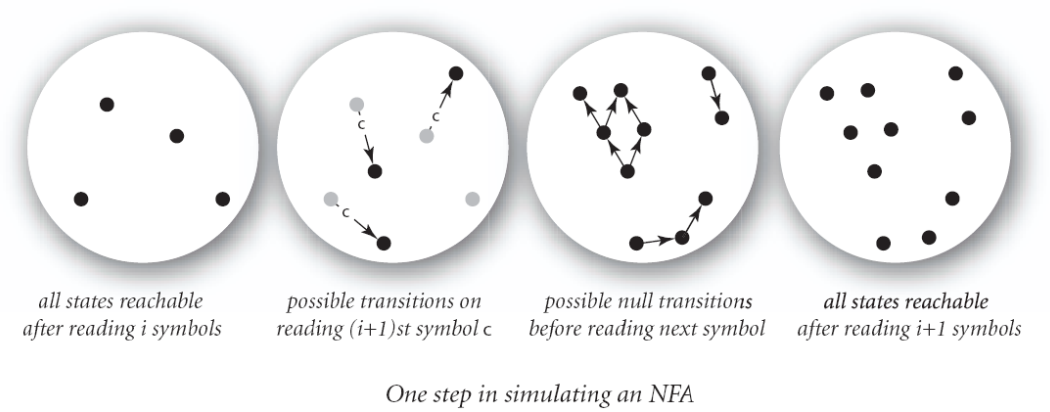
每一步可以走到的状态(reachable),可以用课程之前介绍过的深搜来获得,需要的时间和 E + V 成正比。
public class NFA {
private char[] re; // match transitions
private Digraph G; // epsilon transition digraph
private int M; // number of states
public NFA(String regexp) {
M = regexp.length();
re = regexp.toCharArray();
G = buildEpsilonTransitionDigraph();
}
public boolean recognizes(String txt) {
// states reachable from start by epsilon transitions
Bag<Integer> pc = new Bag<Integer>();
DirectedDFS dfs = new DirectedDFS(G, 0);
for (int v = 0; v < G.V(); v++)
if (dfs.marked(v)) pc.add(v);
for (int i = 0; i < txt.length(); i++) {
// states reachable after scanning past txt.charAt(i)
Bag<Integer> match = new Bag<Integer>();
for (int v : pc) {
if (v == M) continue;
// 匹配时直接加上下一个状态
if ((re[v] == txt.charAt(i)) || re[v] == '.')
match.add(v + 1);
}
// follow epsilon transitions
dfs = new DirectedDFS(G, match); // 拓展上一步的所有状态
pc = new Bag<Integer>();
for (int v = 0; v < G.V(); v++)
if (dfs.marked(v)) pc.add(v);
}
// accept if can end in state M
for (int v : pc)
if (v == M) return true;
return false;
}
public Digraph buildEpsilonTransitionDigraph() {
// 见下一小节
}
}
最坏情况下,在长度为 N 的文本中寻找长度为 M 的模式,需要的时间和 MN 成正比。对于文本中的每个字符,我们都要对 \(\epsilon\) 转移有向图来次深搜,而下面要介绍的构造转移图的方法可以保证其边数不超过 3M,即意味着深搜时间和 M 成正比,所以总共是正比于 MN。
NFA-construction
现在我们再来具体说说如何构造 NFA。
States
NFA 的状态数为 M + 1,用 0 - M 间的整数来表示,最后是接受状态,没什么好说的。

Concatnation
针对连接操作,将表示字符的状态指向下一个状态,即字符匹配时的情况,不用显式构造,见上一节代码。

Parentheses
括号主要是为了下面的闭包和或操作服务的,它自己就直接加条 \(\epsilon\) 转移,表示可以直接到下一状态。
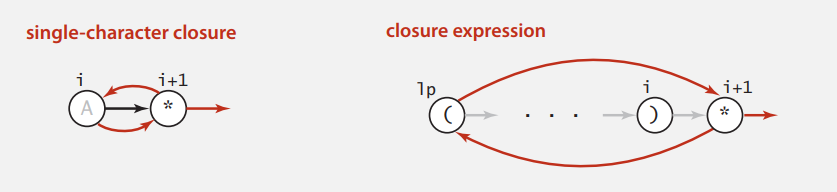
Closure
闭包分为下面两种情况,也很好理解,实现下面再说。
例子里只有第一种情况。
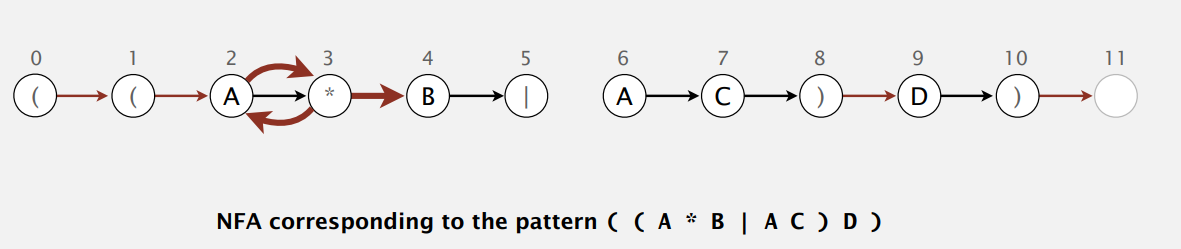
Or
或操作两边应有括号括起才合情合理,所以就这一种情况。
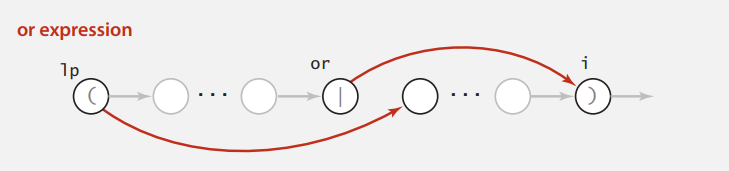
例子再来两条空转移。
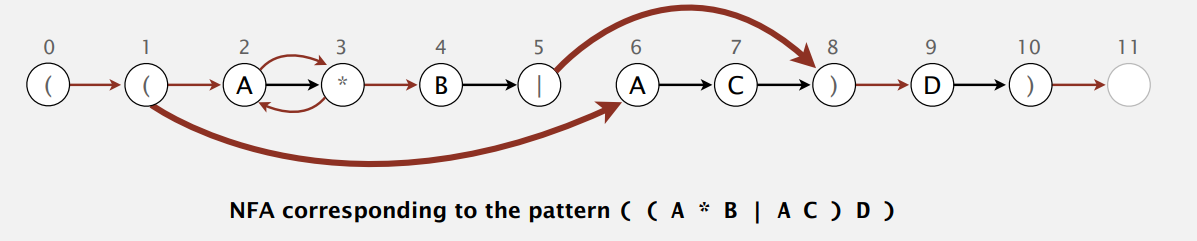
为了实现后面两种跨度较大的转移,我们需要借助栈这一数据结构。扫描正则表达式构造 NFA 时,碰到左括号和或操作符就压入栈(状态编号),碰到右括号就弹出栈顶状态号,如果状态对应的是或操作符,那或操作要加的两条空转移的三个状态号现在都可以知道,因为左括号状态肯定在栈顶现在。而闭包的话,只要向前看一个字符就好,具体看代码。
private Digraph buildEpsilonTrnsitionDigraph() {
Digraph G = new Digraph(M + 1);
Stack<Integer> ops = new Stack<Integer>();
for (int i = 0; i < M; i++) {
int lp = i; // 左括号或当前扫描字符所在状态标号
// left parentheses and |
if (re[i] == '(' || re[i] == '|') ops.push(i);
else if (re[i] == ')') {
int or = ops.pop();
if (re[or] == '|') {
lp = ops.pop();
G.addEdge(lp, or + 1);
G.addEdge(or, i);
}
else lp = or; // 不是或操作就是左括号,更新为闭包服务
}
// closure
// needs 1-character lookahead
if (i < M - 1 && re[i + 1] == '*') {
G.addEdge(lp, i + 1);
G.addEdge(i + 1, lp);
}
// metasymbols
if (re[i] == '(' || re[i] == '*' || re[i] == ')')
G.addEdge(i, i + 1);
}
return G;
}
上面的构造过程,需要的时间和空间都只是正比于 M 的级别。因为,从上面添加边的过程可以看出,对于长度为 M 的正则表达式,每个字符我们最多只有加三条空转移边和两个对栈的操作。
Applications
课程举了挺多例子,这里不做展开。正则表达式模式匹配的起源是 Unix 的命令 grep (Generalized regular expression print,另说 Global search a regular expression and print),而现在正则表达式则已经被内置于许多现代编程系统之中,像 Perl、Python 和 Javascript。


