Programming Assignment 3: Baseball Elimination
编程作业三
作业链接:Baseball Elimination & Checklist
问题简介
这是一个最大流模型的实际应用问题:篮球淘汰赛,设想你现在知道如下的比赛信息:
w[i] l[i] r[i] g[i][j]
i team wins loss left Atl Phi NY Mon
------------------------------------------------
0 Atlanta 83 71 8 - 1 6 1
1 Philadelphia 80 79 3 1 - 0 2
2 New York 78 78 6 6 0 - 0
3 Montreal 77 82 3 1 2 0 -
每条记录包含了队伍编号,队伍名,获胜、失败、总剩余以及和各其他的队伍剩余比赛数目。
于是现在我们想要用这些信息从的数学角度来判断一个队伍是否有可能获得第一,或是已经被数学淘汰了。
来看上面记录的队伍 3,获胜 77 场,还剩下 3 场,于是最多也只能获胜 80 场。但是队伍 0 已经获胜了 83 场,所以队伍 3 是不可能获得第一的。这样的算术是很简单的,但有时也并不简单,我们再来看看队伍 1。队伍 1 最多有可能获胜 83 场,和目前最多获胜数目一样,那有没有可能至少是并列第一名呢。那就要求已经获胜 83 场的队伍 0 输掉接下来的全部比赛,于是队伍 2 在和队伍 0 的 6 场比赛中全部获胜,最终至少获胜 84 场。故从数学上来说,队伍 1 已经被队伍 0 和 2 淘汰了。
可以看出这个问题有时候并没有那么简单,最大流模型可以帮我们来判断复杂情况下某个队伍是否被数学淘汰,首先我们需要把比赛信息转换流量网络(课程给的例图是下面的比赛记录)。
w[i] l[i] r[i] g[i][j]
i team wins loss left NY Bal Bos Tor Det
---------------------------------------------------
0 New York 75 59 28 - 3 8 7 3
1 Baltimore 71 63 28 3 - 2 7 7
2 Boston 69 66 27 8 2 - 0 3
3 Toronto 63 72 27 7 7 0 - 3
4 Detroit 49 86 27 3 7 3 3 -
比如现在我们想知道队伍 4 是否已经被数学淘汰了,要这样构建流量网络。
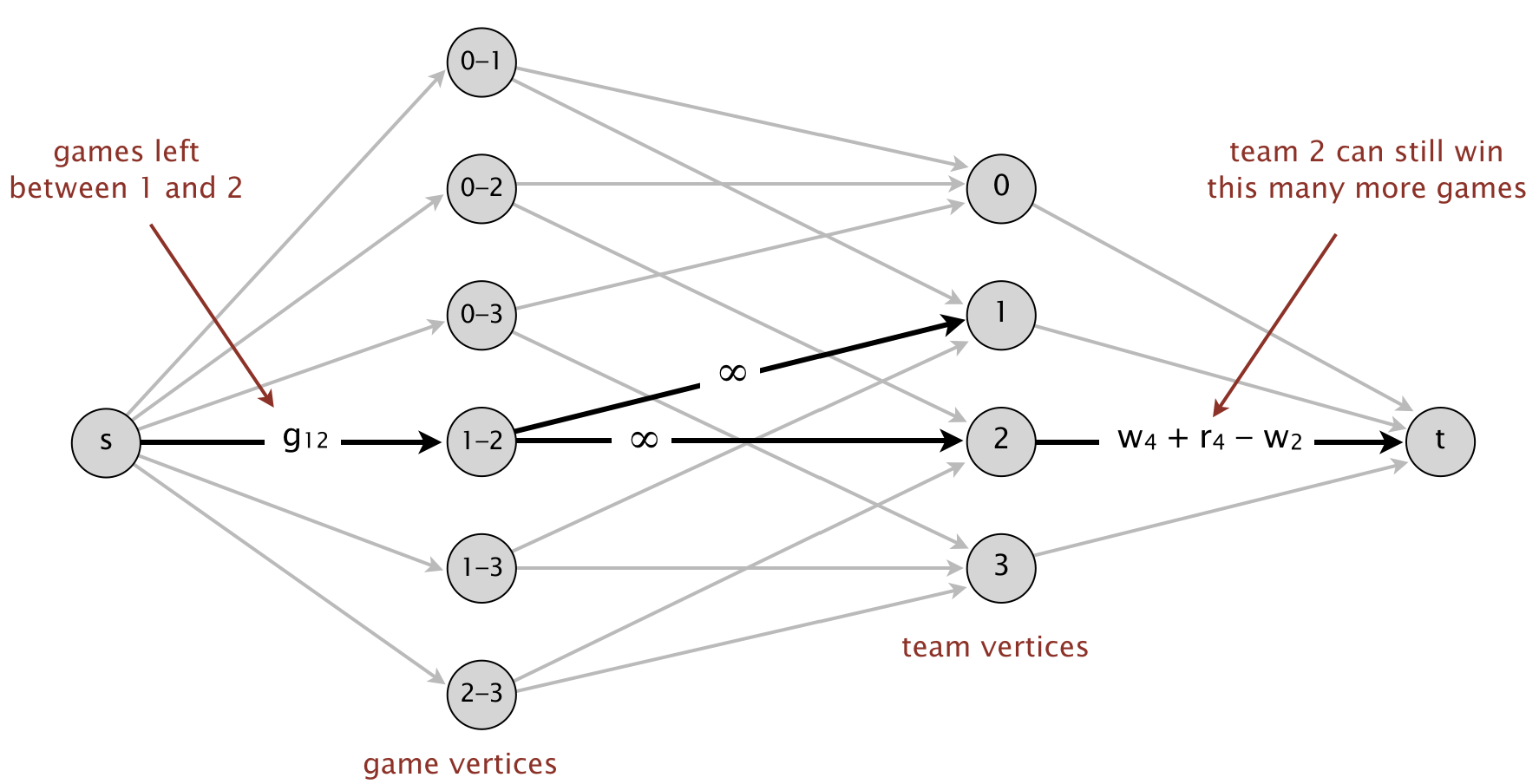
首先肯定要有源点和汇点,这俩就虚拟出来,和比赛记录没关系,剩下的点可以分为队伍点和比赛点。
队伍点表示除去要判断的队伍的其它队伍,这里即队伍 0,1,2,3。比赛点表示不同队伍间的比赛,指向比赛的两个队伍点,边容量没有限制。而源点指向比赛点的边容量为比赛数目,像队伍 0 和队伍 1 还要比 3 次,那就是 3。于是我觉得比赛点 2-3 没必要,因为队伍 2 和 3 没有比赛了,虽然边容量为零也没什么影响其实。这边比赛谁获胜几场,就有多少流量到相应队伍点,挺合理。
然后,重点是队伍点到汇点的边容量。这个流量网络是为了判断队伍 4 是否被数学淘汰,于是乎举个例子,队伍点 2 到汇点的边容量为 w4 + r4 - w2,就是队伍 4 可能的最高获胜数目减去队伍 2 已经获胜的数目,相当于限制队伍 2 最高获胜次数不能大于队伍 4 的。
于是在这样的流量网络上跑 Ford-Fulkerson 算法,如果最后跑出来的最大流(能到汇点的流量最大值)和源点发出的边的总容量相等(其他队伍能在总获胜次数限制不大于队伍 4 的情况下完成剩下的所有比赛),那么队伍 4 就还没被数学淘汰。
如果最大流达不到要求,那么队伍 4 就被数学淘汰。这时最小割里源点一边的队伍点集合,可以帮我们解释队伍 4 为什么被数学淘汰。上面例子的队伍 4 是不可能拿第一的,它最多只能获胜 76(w:49 + r:27) 场。考虑最小割里源点一边的队伍集合 {0, 1, 2, 3},它们总的已获胜数目为 278 = 75 + 71 + 69 + 63,它们之间还有 27(3 + 8 + 7 + 2 + 7 ) 场比赛,于是每个队伍最后平均获胜数目也有 76.5 = (27 + 278) / 4。所以队伍 4 已经被数学淘汰了。
任务摘要
public class BaseballElimination { // create a baseball division from given filename in format specified below public BaseballElimination(String filename) // number of teams public int numberOfTeams() // all teams public Iterable<String> teams() // number of wins for given team public int wins(String team) // number of losses for given team public int losses(String team) // number of remaining games for given team public int remaining(String team) // number of remaining games between team1 and team2 public int against(String team1, String team2) // is given team eliminated? public boolean isEliminated(String team) // subset R of teams that eliminates given team; null if not eliminated public Iterable<String> certificateOfElimination(String team) }
摘自:Baseball Elimination,略去很多细节。
问题分析
照着 Checklist 里建议的编程步骤,一步步下来,总得来说,问题不大。
数据存储
一开始队伍名称存在字符串数组里,比赛数据则存在二维整型数组,二者数组下标即体现了对应关系。最初一些简单方法的实现都还可以支持,teams() 需要另返回一个可迭代的字符串对象。
在后来的实现中,从队伍名快速获取队伍比赛数据的需求愈发明显。最初的存储需要遍历字符串数组找到队伍编号,然后才能找到对应的比赛数据,略麻烦。于是乎,想到了课程里的 [ST.java](file:///C:/Users/Archeroc/AppData/Local/Temp/360zip$Temp/360$0/edu/princeton/cs/algs4/ST.java.html),把数据存在 allData<String, int[]> 里,就可以从键(队伍名)快速获取队伍数据啦。而且其它方法也有简化,像 teams() 直接返回 allData.keys() 就好。
再后来,在构建流量网络时需要队伍的编号,而集合没有什么顺序,可迭代对象返回的顺序每次也不一定一样。于是,在比赛记录的整数数组最后加一位保存队伍编号,按读入数据时的顺序来记录就好。构建网络时,先迭代存储数据生成按编号存储的辅助数组 String[] teams,构建网络时才没有那么乱。
构建网络
流量网络用邻接表表示,网络中的点其实就有编号,于是前面的就给队伍点,天然对应队伍编号。然后,最后两个给源点和汇点,构建的时候经常用到,这样好输入。最后,中间的点就给各个比赛。
有了上面说的辅助数组,构建网络的过程就很清晰了,问题不大,跑 FF 算法也很顺利,直接上代码:BaseballElimination.java
测试结果