Maximum Flow and Minimum Cut
最大流最小割
Introduction
Mincut Problem
最小割问题,输入是带权有向图,有一个源点 s(source)和一个汇点 t(target),边的权重在这里称作容量(capacity),是个正数。
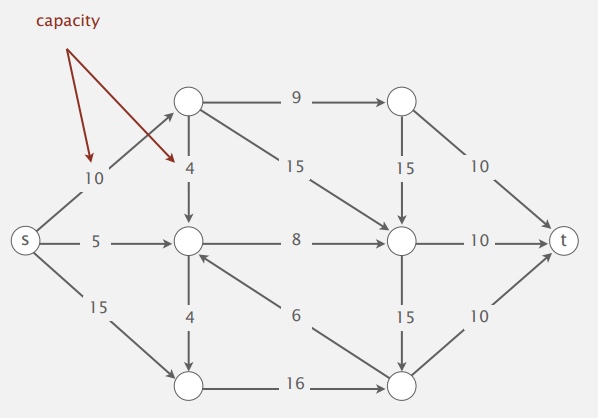
st-cut(cut): 把图的点分成两个集合 A 和 B,源点 s 和汇点 t 分别属于集合 A 和 B。
capacity: 从集合 A 的点指向集合 B 的点的边的权重之和,如下图。
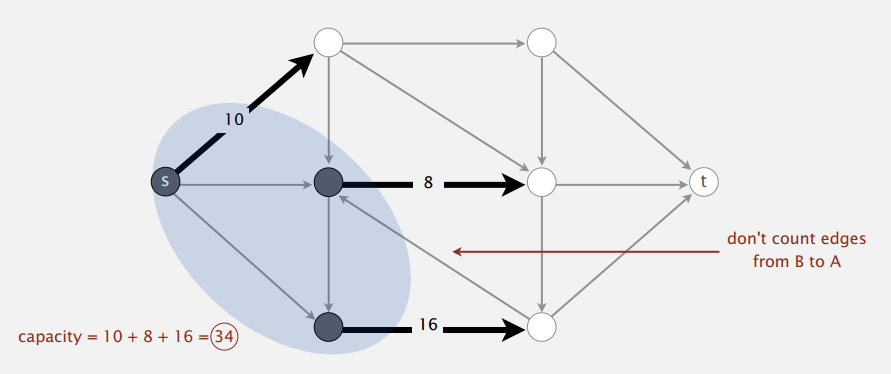
最小割问题就是找到使 capacity 最小的划分(st-cut),即阻隔从源点到汇点的最小代价。课程举了一个军事补给线的例子,可以用于找到切断敌方军队补给的最小代价。
Maxflow Problem
最大流问题,输入差不多,边一样有容量,多了个流(flow)的概念。把边想象成水管,容量就是设计的最大的流量,流就是实际的流量,显然后者不能大于前者。

为了简化问题,我们假定源点只有流出量,汇点只有流入量,二者相等,也是这张图流的值(总流量)。对于图中的点来说,除了源点和汇点,流入量和流出量是一样的,净流量为零。最大流问题即找出从源点通过图能够传到汇点的最大流的值,满足边的容量限制,各个点要怎么分配流量。应用例子可以反着来,通过补给线能给前线最大提供多少补给,又该怎么调配。
令人惊讶的是,最大流问题和最小割问题是对偶的(dual),若前者有最优解,则后者的最优解存在且相等。
Ford-Fulkerson Algorithm
Ford-Fulkerson 算法是一类计算网络流的最大流的贪心算法,按增广路径的寻找方式又有几种不同的实现方式。
大致过程: 将图中的边视作无向的,边的流量初始为 0,然后寻找从源点 s 到汇点 t 的增广路径,在路径上:
- 增加容量未满的正向边上的流量。
- 减少流量非空的反向边上的流量。
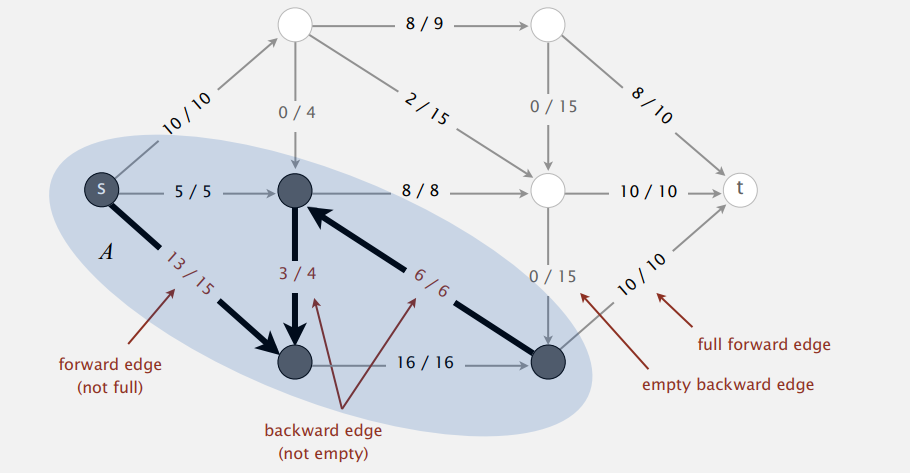
增广路径即存在未满正向边或非空反向边的路径,正向边即边的方向和路径一样,反向边反之。增加源点到汇点方向的正向边流量,减少相反方向的反向边流量,直到没有增广路径,感觉上也是最后就能算出最大流。看个例子:
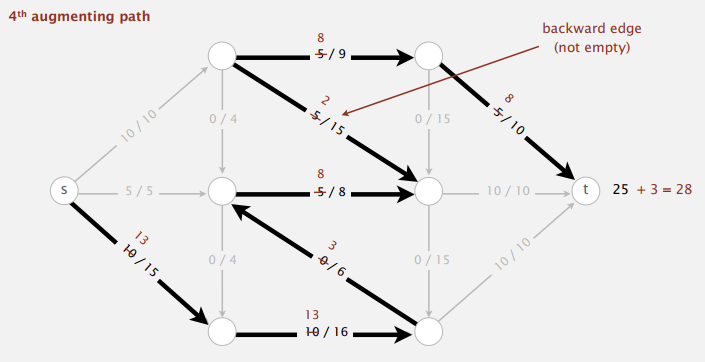
这条源点到汇点的路径上有很多容量未满的正向边,还有条流量非空的反向边。为了知道增加(减少)多少流量,我们需要计算正向边剩余的可用容量以及反向边被占用的流量,从中找出最小值。上图中不难看出最小值是三,于是正向边流量加三,反向边流量减三,最终到汇点的流量增加三,而图中各点的净流量仍然为零。
在关于流量性质的一定技术性限制之下,无论我们如何选择路径,该方法总能找出最大流量,它的意义在于证明了所有同类算法的正确性。
Maxflow-Mincut Theorem
最大流-最小割定理可以证明 Ford-Fulkerson 算法的正确性,首先我们要了解下流和割的关系,下面是一些概念。
flow across: 跨切分流量,指源点所在集合 A 到汇点所在集合 B 的净流量,数值上等于:
\(\sum\limits_{u\in A, v\in B}f_{uv}i_{uv} - \sum\limits_{u\in B, v\in A}f_{uv}i_{uv}\),其中 \(f_{uv}\) 指边 u->v 上的流量;当边 u->v 存在时, \(i_{uv}\) 等于 1,否则为 0。
样例:(灰色的点属于集合 A,白色则是集合 B)
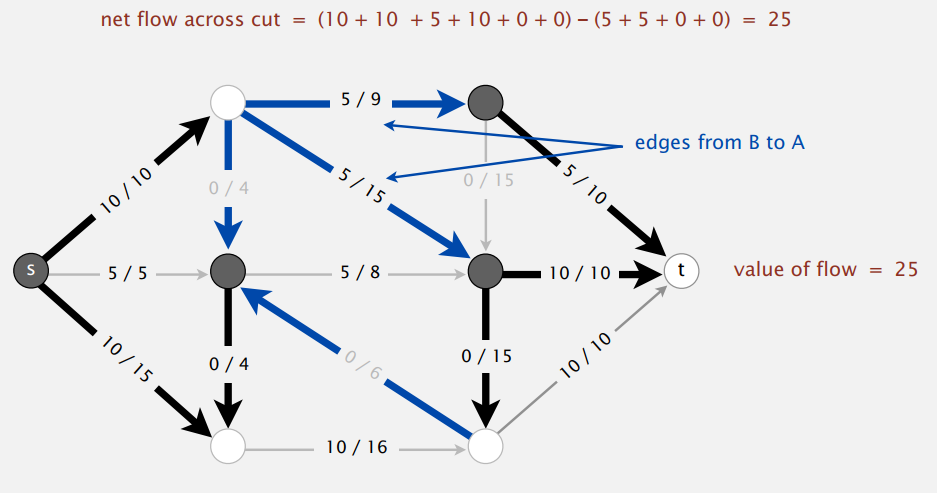
Flow -value lemma: 流-值引理,对于流量网络的任意 st-cut,跨切分流量总是等于网络的总流量。
实际上跨切分流量就是从源点流到汇点的有效的流量总值,即网络总流量。也可以对集合 B 的规模来归纳证明:当 B = {t} 时,跨切分流量即为汇点的流入量,等于网络总流量;因为网络中其它点的流入量等于流出量,不管你怎么把集合 A 中的点移入集合 B ,跨切分流量都不会变的,会一直等于网络总流量。
weak duality: 弱对偶性,对于流量网络的任意 st-cut,割的容量不小于网络的总流量。
最小割问题的容量就是跨切分流量计算式的前半部分的上限,自然不会小于跨切分流量,也不会小于网络总流量。
铺垫到此结束,最大流-最小割定理其实就是说流量网络的最大流等于最小割的容量,通过证明下面的三种情形是等价的来解释:
- 存在一个容量等于流量网络总流量 f 的 st-cut。
- 流量网络总流量 f 是最大流。
- 流量网络已经没有可以优化的增广路径了。
1->2: 假设一个 st-cut,不妨记为 (A, B),它的容量等于 f。由 weak duality 可知网络的总流量不大于 (A, B) 的容量,那么 f 就是网络的最大流啦。
2->3: 假设网络中还存在增广路径,那么 f 就还可以更大,与 f 是最大流矛盾。
3->1: 假设现在流量网络已经没有增广路径,考虑这样一个 st-cut:集合 A 包含所有源点通过未饱和正向边或是非空反向边能到达的点(无向路径),剩下点构成集合 B。因为网络中没有增广路径(从源点到汇点的无向路径,要求含有未饱和正向边或是非空反向边),所以集合 A 中不会包含汇点,这是个可行的 st-cut。而这个 st-cut 的容量等于跨切分流量,因为根据我们的构造原则,集合 A 到集合 B 的边不是饱和正向边就是空的反向边,flow-across 计算式后半部分为零。再根据 flow-value lemma 有网络总流量等于跨切分流量,所以这个 st-cut 的容量等于网络总流量。
综上,三种情形是等价的。
3->2 即可说明 Ford-Fulkerson 方法可以正确计算网络的最大流。对于同一个流量网络来说,最小割的容量和网络中现在实际的流量并没有关系,一个 st-cut 对应一个容量,不会因为网络流量的变化而有所改变。不妨假设现在网络达到了最大流,按照上面证明 3->1 中的方法可以构造出容量和最大流相等的 st-cut,根据 weak duality 可知容量等于网络流量的是最小割,没有其它更小的 st-cut 方案了,不管网络的实际流量是不是最大。所以最大流-最小割定理是正确的,我们可以通过计算最大流来求最小割。最后再来张例图:
Running Time Analysis
我们考虑边的容量都是整数的流量网络。
-
对这样的流量网络,Ford-Fulkerson 方法计算的流是整数。
边的容量都是整数,限制的瓶颈容量自然也是整数,而边上的流都是加减瓶颈容量得到的,最终还是整数。
-
增广路径的数目小于最大流的值。
因为每条增广路径至少会把网络总流量增加 1。
-
Integrality theorem: 完整性,这样的网络存在着整数值的最大流。
整数网络增广路径的数目是有限的,FF 算法肯定会终止,计算出那个最大流。
附: FF 算法无法终止的样例,我是看不大懂其实,这里也不深究。
就算是整数网络,增广路径最坏情况下也会等于最大流的值,像下面的例子:
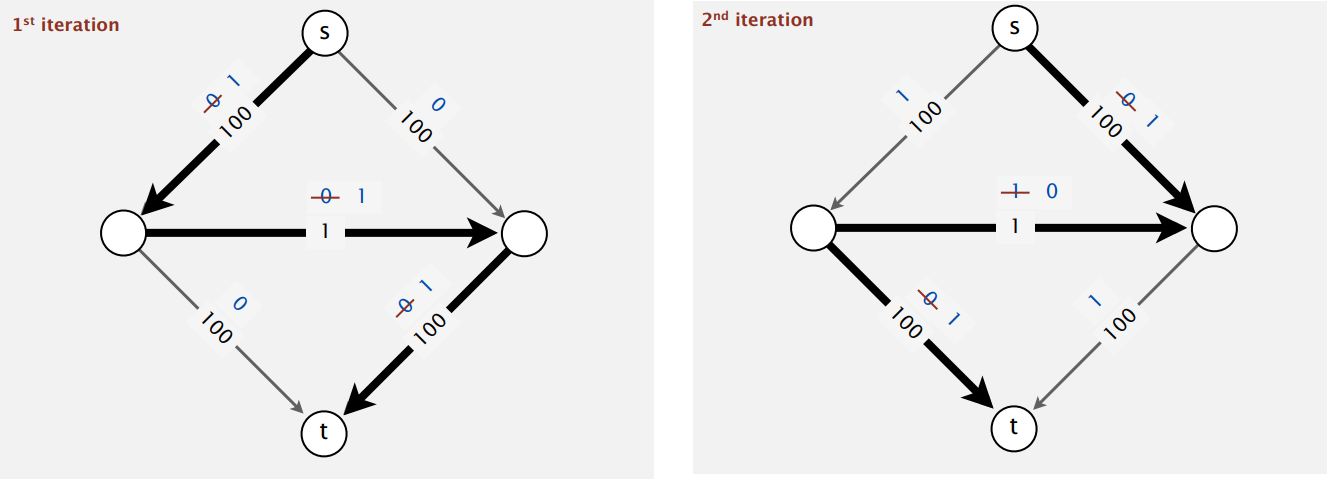
上面两条路径一直交替,要两百次才能算出最大流。我们可以改变增广路径的搜索策略来避免这种情况,像是最短路径法(BFS),或是最大容量路径法等:

不同搜索策略下增广路径数的上限如下:
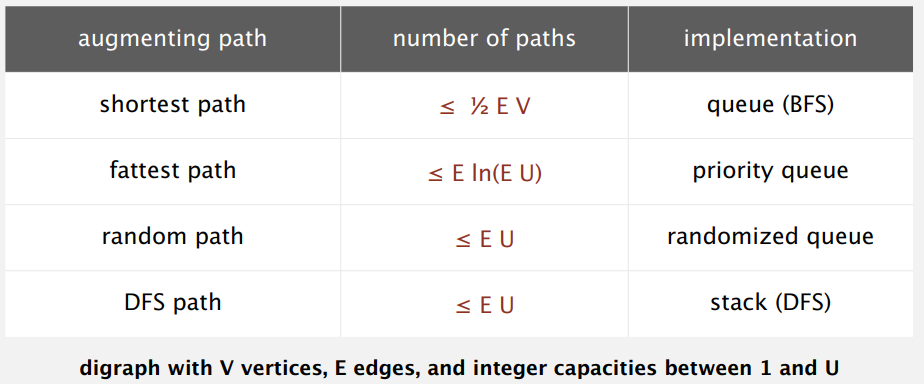
这些都是很保守的值,实际使用中基本上不会达到这种数量。
Java Implementation
Residual Network
流量网络的边既有容量又有流量,势必需要新的数据类型来表示边,同时网络本身也有一种有用的其它表示,称为剩余网络(residual network)。
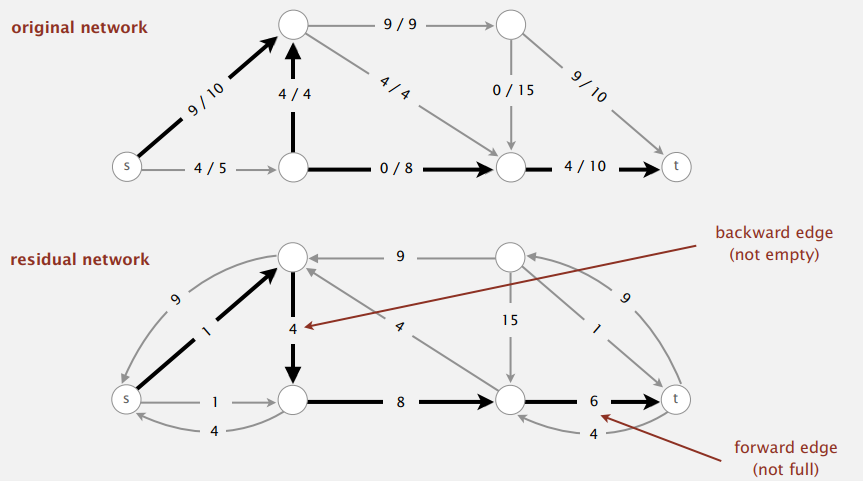
流量网络边的流量在剩余网络中为反向的同等权重的边,若边未饱和,则剩余网络中还有同向的剩余流量权重边。这样表示的好处在于:流量网络中的增广路径在剩余网络中变为有向路径,会让我们的代码更加简洁优雅。
Flow Edge
public class FlowEdge {
private final int v, w; // from and to
private final double capacity;
private double flow;
// create a flow edge v->w
public FlowEdge(int v, int w, double capacity) {
this.v = v;
this.w = w;
this.capacity = capacity;
}
public int from() {
return v;
}
public int to() {
return w;
}
public double capacity() {
return capacity;
}
public double flow() {
return flow;
}
// other endpoint
public int other(int vertex) {
if (vertex == v) return w;
else if (vertex == w) return v;
}
// residual capacity toward v
public double residualCapacityTo(int vertex) {
// backward edge
if (vertex == v) return flow;
// forward edge
else if (vertex == w) return capacity - flow;
}
// add delta flow toward v
public void addResidualFlowTo(int vertex, double delta) {
// backward edge
if (vertex == v) flow -= delta;
// forward edge
else if (vertex == w) flow += delta;
}
}
对于正向边来说,它的剩余流量即容量减去流量,而反向边则是流量,实际上就是增加网络总流量的潜力值。
Flow NetWork
public class FlowNetwork {
private final int V;
private Bag<FlowEdge>[] adj;
public FlowNetwork(int V) {
this.V = V;
adj = (Bag<FlowEdge>[]) new Bag[V];
for (int v = 0; v < V; v++)
adj[v] = new Bag<FlowEdge>();
}
public void addEdge(FlowEdge e) {
int v = e.from();
int w = e.to();
adj[v].add(e); // add forward edge
adj[w].add(e); // add backward edge
}
public Iterable<FlowEdge> adj(int v) {
return adj[v];
}
}
依然是邻接表,当做无向图来存,既有正向情况,又有反向情况,但实际边对象只有一个。
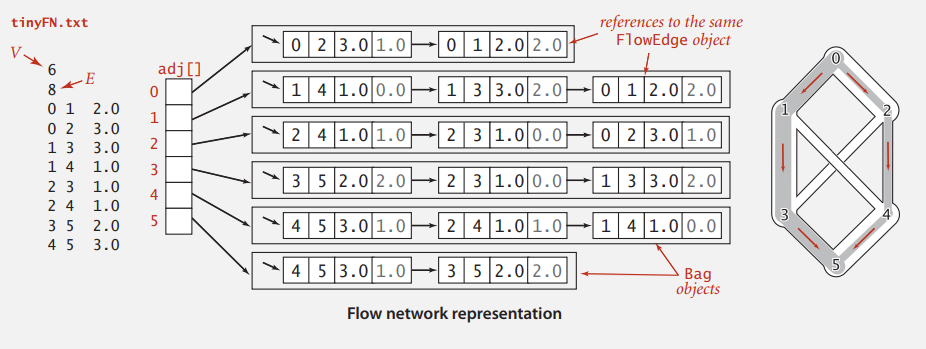
Ford-Fulkerson
public class FordFulkerson {
private boolean[] marked; // true if s->v path in residual network
private FlowEdge[] edgeTo; // last edge on s->v path
private double value; // value of flow
public double value() {
return value;
}
// is v reachable from s in residual network?
public boolean inCut(int v) {
return marked[v];
}
public FordFulkerson(FlowNetwork G, int s, int v) {
value = 0.0;
while (hasAugmentingPath(G, s, t)) {
// compute bottlenack capacity
double bottle = Double.POSITIVE_INIINITY;
for (int v = t; v != s; v = edgeTo[v].other(v))
bottle = Math.min(bottle, edgeTo[v].residualCapacityTo(v));
for (int v = t; v != s; v = edgeTo[v].other(v))
edgeTo[v].addResidualFlowTo(v, bottle);
value += bottle;
}
}
private boolean hasAugmentingPath(FlowNetwork G, int s, int t) {
edgeTo = new FlowEdge[G.V()];
marked = new boolean[G.V()];
Queue<Integer> queue = new Queue<Integer>();
queue.enqueue(s);
marked[s] = true;
// BFS
while (!queue.isEmpty()) {
int v = queue.dequeue();
for (FlowEdge e : G.adj(v)) {
int w = e.other(v);
// found path from s to w i the residual network?
if (e.residualCapacityTo(w) > 0 && !marked[w]) {
edgeTo[w] = e;
marked[w] = true;
queue.enqueue(w);
}
}
}
return marked[t];
}
}
注: 上面贴出来的只是关键部分,完整的在 boosite-6.4 可以找到。
Applications
最大流模型有着广泛的应用,比如说二分匹配(bipartite matching)问题。
假设有 N 个学生从总共 N 个的公司收到了一些 offer,每个公司只收一人,怎样每个学生都能有工作呢。
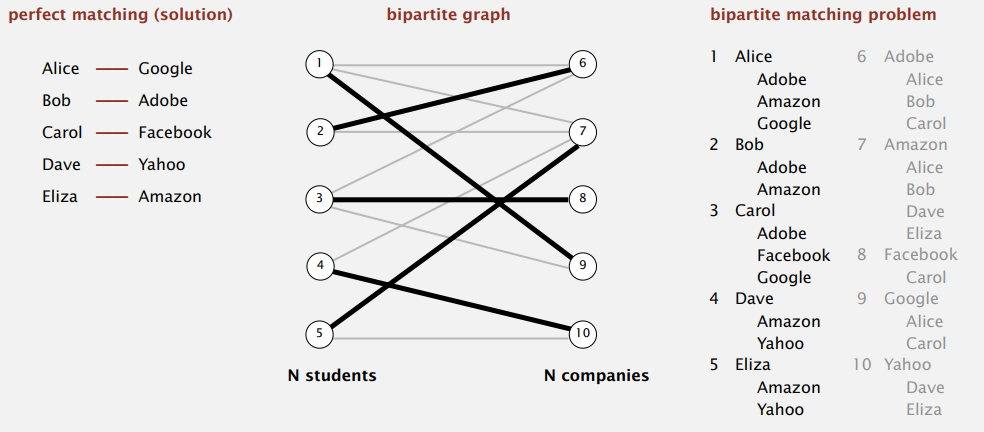
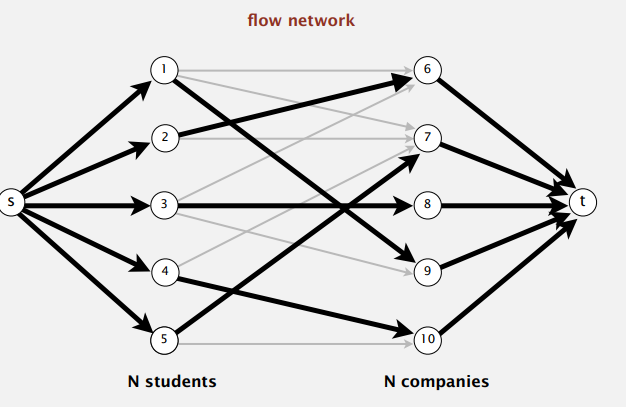
最大流模型就可以帮我们找到完美匹配。像下图那般构造流量网络,s 点到学生的边容量为 1,公司到 t 点的边容量也为 1,学生与公司之间的边容量则没有限制。存在完美匹配的话,FF 算法找到的最大流的值即为 N。
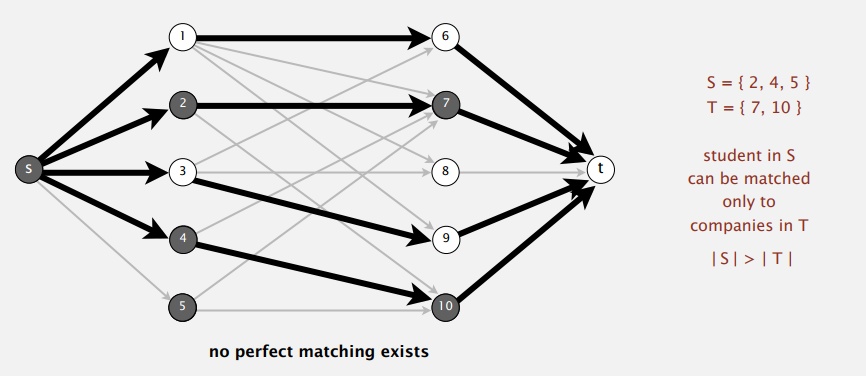
也有可能不存在完美匹配:设想学生中有个集合 S 只收到了公司集合 T 中的 offer,要是前者大于后者,自然无法一一匹配。此时,最小割也可以帮我们找到相应的集合 S 和集合 T。
最大流模型还有很多很多其它应用,相应的研究还在进行,有个篮球淘汰赛方面的应用会在编程作业里再说,这里就不讲啦。


