Shortest Paths

最短路径

APIs

带权有向图中的最短路径，这节讨论从源点（s）到图中其它点的最短路径（single source）。

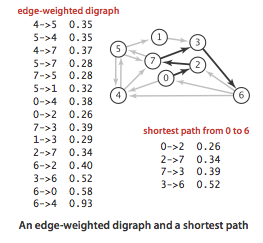
shortest-path

Weighted Directed Edge API

需要新的数据类型来表示带权有向边。

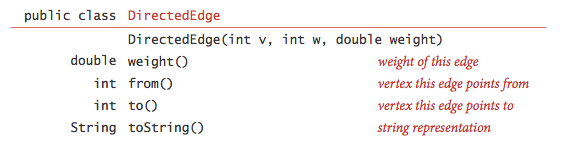
directed-edge-api

Weighted Directed Edge：implementation

public class DirectedEdge {
    private final int v, w;
    private final double weight;

    public DirectedEdge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    public int from() {
        return v;
    }

    public int to() {
        return w;
    }

    publiv int weight() {
        return weight;
    }
}

习惯上处理边 e 的时候先获取端点：int v = e.from(), w = e.to();

Edge-weighted Digraph API

edge-weighted-digraph-api

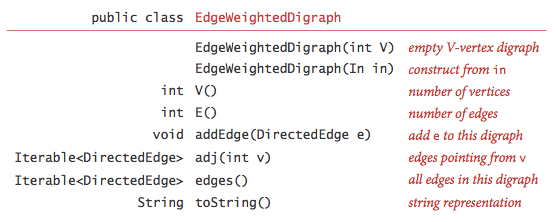
依然是使用邻接表表示，保存的是指向边对象的引用。

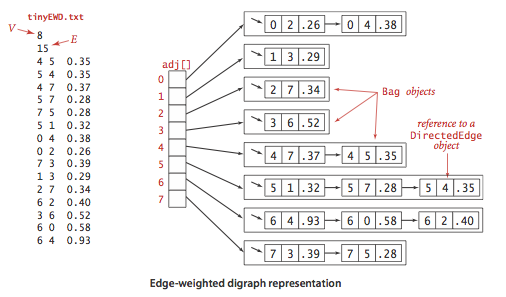
edge-weighted-digraph-representation

Edge-weighted Digraph:implementation

public class EdgeWeightedDigraph {
    private final int V;
    private final Bag<DirectedEdge>[] adj;

    public EdgeWeightedDigraph(int V) {
        this.V = V;
        adj = (Bag<DirectedEdge>[]) new Bag[V];
        for (int v = 0; v < V; v++)
            adj[v] = new Bag<DirectedEdge>();
    }

    public void addEdge(DirectedEdge e) {
        int v = e.from();
        adj[v].add(e);
    }

    public Iterable<DirectedEdge> adj(int V) {
        return adj[v];
    }
}

Single-source Shortest Paths API

sp-api

测试用例

SP sp = new SP(G, s);
for (int v = 0; v <G.V(); v++) {
    StdOut.printf("%d to %d (%.2f): ", s, v, sp.distTo(v));
    for (DirectedEdge e : sp.pathTo(v))
        StdOut.print(e + " ");
    StdOut.println();
}

运行示例

sp-sample

注：上述内容，详细的可以参考 booksite-4.4。

Shortest-paths Properties

Data Stuctures

这里讨论单点最短路径，我们用两个以点为索引的数组来表示最短路径树（SPT）。

spt

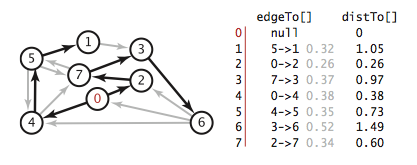
edgeTo[i] 表示从点 0 到点 i 的最短路径上的最后一条边，用来还原最短路径，edgeTo[0] 记为 null。distTo[i] 即表示从点 0 到点 i 的最短路径长度，distTo[0] 为 0。

public double distTo(int v) {
    return distTo[v];
}

public Iterable<DirectedEdge> pathTo(int V) {
    Stack<DirectedEdge> path = new Stack<DirectedEdge>();
    for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from])
        path.push(e);
    return path;
}

Relaxation

我们的最短路径 API 的实现都基于一个被称为松弛（relaxation）的简单操作。想象把一根橡皮筋沿最短路径拉长，找到更短的路径，也就“松弛”了这根橡皮筋。

Edge

放松边 v->w 就是要检查源点 s 到点 w 经过这条边是否会更短。

private void relax(DirectedEdge e) {
    int v = e.from(), w = e.to();
    if (distTo[w] > distTo[v] + e.weight()) {
        distTo[w] = distTo[v] + e.weight();
        edgeTo[w] = e;
    }
}

下图中，左边例子称为边失效，右边则说放松是成功的。

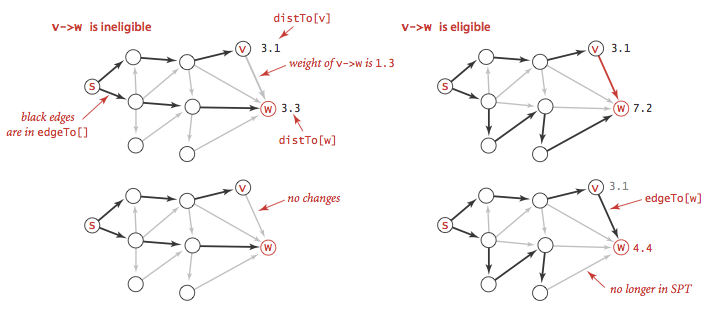
relaxation-edge

Vertex

点的松弛即放松由其发出的所有边。

private void relax(EdgeWeightedDigraph G, int v) {
    for (DirectedEdge e : G.adj(v)) {
        int w = e.to();
        if (distTo[w] > distTo[v] + e.weight()) {
            distTo[w] = distTo[v] + e.weight();
            edgeTo[w] = e;
        }
    }
}

Shortest-paths Optimality Conditions

最优性条件：当且仅当对于任意从点 v 到点 w 的边 e，满足 distTo[w]\(\leqslant\)distTo[v]+e.weight()（没有可以放松的有效边），那么 distTo[w] 是从 s 到 w 的最短路径长度。

证明

  • 必要性

    假设 distTo[w] 是 s 到 w 的最短路径。若存在边 e(v->w) 有 distTo[v]+e.weight()<distTo[w]，显然从 s 到 v 再经 e 到 w 更短，矛盾。

  • 充分性

    假设 s=\(v_{0}\)->\(v_{1}\)->\(v_{2}\)->...->\(v_{k}\)=w 是 s 到 w 的最短路径，其权重记为 \(OPT_{sw}\)，\(e_{i}\) 表示路径上的第 i 条边，有：

    distTo[\(v_{1}\)] \(\leqslant\) distTo[\(v_{0}\)] + \(e_{1}\).weight()

    distTo[\(v_{2}\)] \(\leqslant\) distTo[\(v_{1}\)] + \(e_{2}\).weight()

    ...

    distTo[\(v_{k}\)] \(\leqslant\) distTo[\(v_{k-1}\)] + \(e_{k}\).weight()

    综合这些不等式并去掉 distTo[\(v_{0}\)] = distTo[s] = 0:

    distTo[w] = distTo[\(v_{k}\)] \(\leqslant\) \(e_{1}\).weight() + \(e_{2}\).weight() + ... + \(e_{k}\).weight() = \(OPT_{sw}\)

    又因为 distTo[w] 是从 s 到 w 的某条路径的长度，不会比最短路径更短，所以下列式子成立。

    \(OPT_{sw} \leqslant\) distTo[w] \(\leqslant OPT_{sw}\)

Generic Shortest-paths Algorithm

由上述最优性条件马上可以得到一个计算单点最短路径问题的 SPT 的通用算法：

  • 将 distTo[s] 初始化为 0，其它 distTo[] 元素初始化为无穷大。
  • 重复放松图 G 中的任意边，直到不存在有效边为止（满足最优性条件）。

Pf

  • 算法会把 distTo[v] 赋值成某条从 s 到 v 的路径长，且 edgeTo[v] 是该路径的最后一条边。
  • 对于 s 可到达的点 v，distTo[v]初始为无穷大，肯定存在有效边。
  • 每次成功的放松都会减少某些 distTo[v]，distTo[v] 减少的次数是有限的。

注：暂时不考虑负权重。

通用算法没有指定边放松的顺序，它为我们提供了证明算法可以计算 SPT 的方式：证明算法会放松所有边直到没有有效边。

Dijkstra's Algorithm

Dijkstra 算法采用和 Prim 算法构建 MST 类似的策略来构建 SPT：每次添加的都是离起点最近的非树顶点。

dijkstra-sample-graph

从起点 s(0) 开始，维护两个数组 distTo 和 edgeTo 来表示 SPT，先把 distTo[0] 置为 0.0，其它 distTo 元素置为无穷大，edgeTo[0] 置为 null。

最初 distTo 数组中最小的非树点（离 SPT 最近的非树顶点）即是 distTo[0]，把点 0 加入 SPT 并进行放松操作。其它 distTo 被初始化为无穷大，点 0 发出的都是有效边，更新对应的 distTo 和 edgeTo 元素。

现在 distTo 数组中最小的是非树顶点是 distTo[1]（显然还需要索引优先队列来帮我们快速获取离 SPT 最近的非树顶点），加入 SPT 并放松点 1。distTo[2] 和 distTo[3] 初始更新，边 1-7 无效。

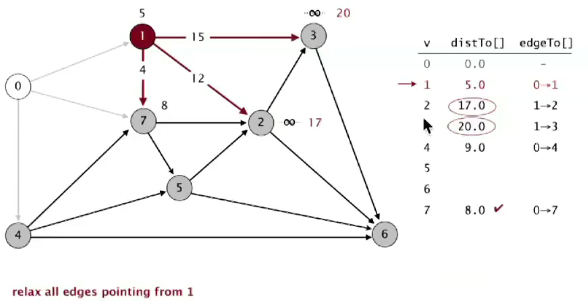
dijkstra-sample1

现在点 7 是离 SPT 最近的非树点，加入 SPT 并放松，边 2-7 有效，更新 distTo[2]，edgeTo[2] 变为 7->2。

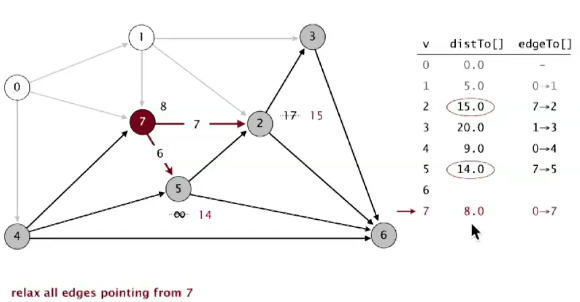
dijkstra-sample2

每次挑离 SPT 最近的非树点加入 SPT 并进行放松操作，直到可到达的点都被加入 SPT，也就完成了计算。

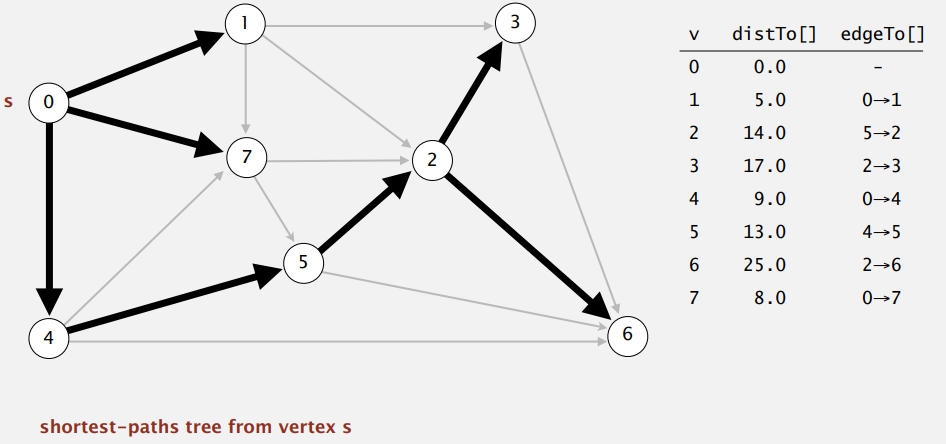
dijkstra-sample-result

s 可到达的点都只会被放松一次，当 v 被放松时，有 distTo[w]\(\leqslant\)distTo[v]+e.weight()，而且该不等式在算法结束前都会成立，因为：

  • distTo[w] 不会增加。因为放松操作只有可能减少 distTo[w]。
  • distTo[v] 不会改变。边的权重非负，我们每次选择的又都是最小的 distTo[] 值，后面的放松操作不可能使任何 distTo[] 的值小于 distTo[v]。

满足最优性条件，所以 Dijkstra 算法可以解决边权重非负的加权有向图的单点最短路径问题。

Dijkstra: Java Implementation

public class DijkstraSP {
    private DirectedEdge[] edgeTo;
    private double[] distTo;
    private IndexMinPQ<Double> pq;

    public DijkstraSP(EdgeWeightedDigraph G, int s) {
        edgeTo = new DirectedEdge[G.V()];
        distTo = new double[G.V()];
        pq = new IndexMinPQ<Double>(G.V());

        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;

        pq.insert(s, 0.0);
        while (!pq.isEmpty()) {
            int v = pq.delMin();
            for (DirectedEdge e : G.adj(v))
                relax(e);
        }
    }

    private void relax(DirectedEdge e) {
        int v = e.from(), w = e.to();
        if (distTo[w] > distTo[v] + e.weight()) {
            distTo[w] = distTo[v] + e.weight();
            edgeTo[w] = e;
            if (pq.contains(w)) {
                pq.decreaseKey(w, distTo[w]);
            } else {
                pq.insert(w, distTo[w]);
            }
        }
    }
}

时间复杂度取决于优先队列的实现，二叉堆的话是 \(ElogV\) 级别。

Edge-weighted DAGs

对于带权无环有向图（DAG）我们有比 Dijkstra 更简单的算法：按图的拓扑排序来放松点，它能在线性时间内计算 SPT，能处理负权重，还可以用来找出最长路径。

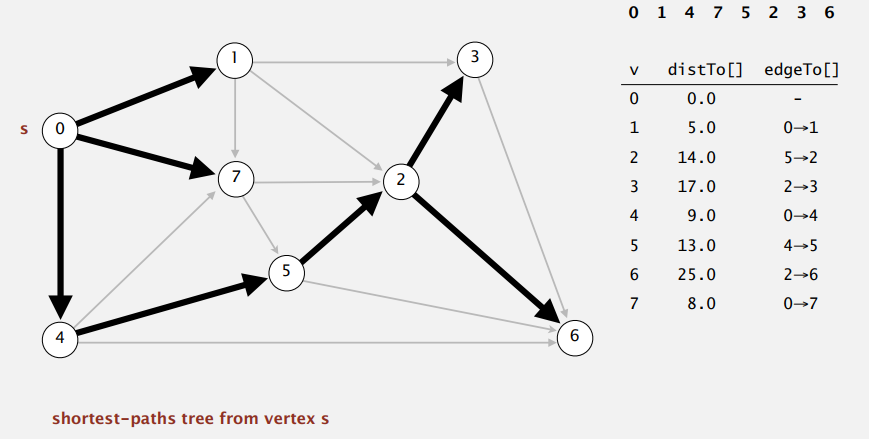
edge-weighted-dag-easy-spt

直接按拓扑排序放松点，最终的 SPT 和 Dijkstra 算法跑的一样，还不需要优先队列，时间复杂度是 \(E+V\) 级别。

证明其正确性也和 Dijkstra 类似，它也会满足最优性条件：

  • 每条边 e(v->w) 只会被放松一次（放松点 v 时），然后有不等式：distTo[w]\(\leqslant\)distTo[v]+e.weight()。

  • 不等式在算法结束前都会成立，因为：

    1. distTo[w] 不会增加，因为放松只可能减少 distTo[] 的值。
    2. distTo[v] 不会改变，因为按拓扑顺序放松，指向点 v 的边不会在点 v 被放松之后放松。

  • 因此，算法结束时满足最短路径的最优性条件，可以正确计算 SPT。

public class AcyclicSP {
    private DirectedEdge[] edgeTo;
    private double[] distTo;

    public AcylicSP(EdgeWeightedDigraph G, int s) {
        edgeTo = new DirectedEdge[G.V()];
        distTo = new double[G.V()];

        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;

        Topological topological = new Topological(G);
        for (int v : topo;ogical.order())
            for (DirectedEdge e : G.adj(v))
                relax(e);
    }
}

这种处理无环有向图最短路径问题的算法，可以被用于调整图片大小，且图片不会失真。

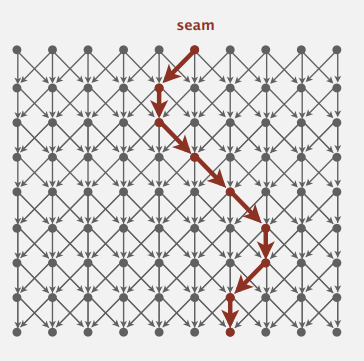
dag-sp-appication-picture

把图片的像素点当做图的点，每个点和下层的三个临近点相连，能量函数根据像素点周围的八个点计算其权重，调整大小时就把最短路径（路径上点权重总和最小）上的像素点去掉。

Longest Paths

拓扑排序算法可以处理负权重边（Dijkstra 要非负才能满足最优性条件），那么我们把边权重取负后再跑，得到的就是最长路径。

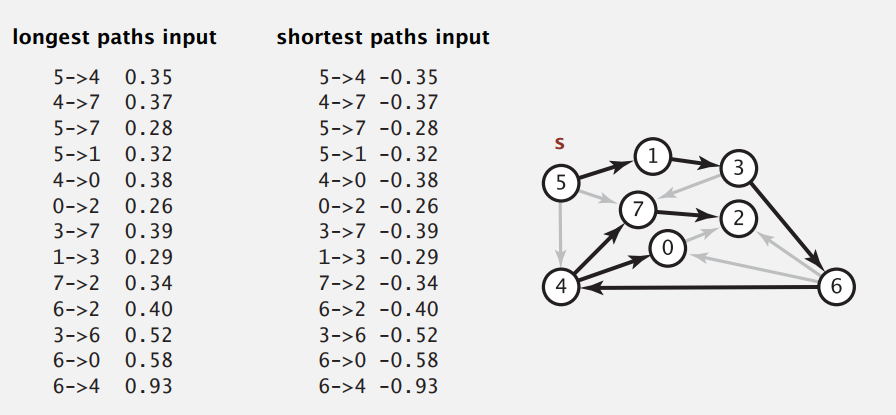
longest-path-topological

最长路径可以应用于平行任务调度问题。

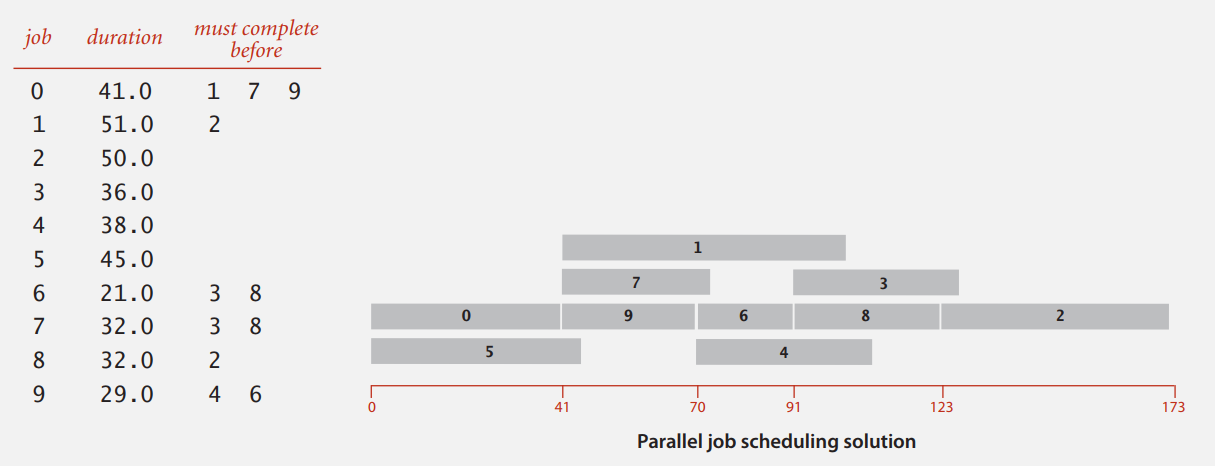
parallel-job

这个并行任务调度有优先级的限制，比如任务 0 必须在任务 1 之前完成，实际应用中很常见，像你要装好车门才能喷漆。

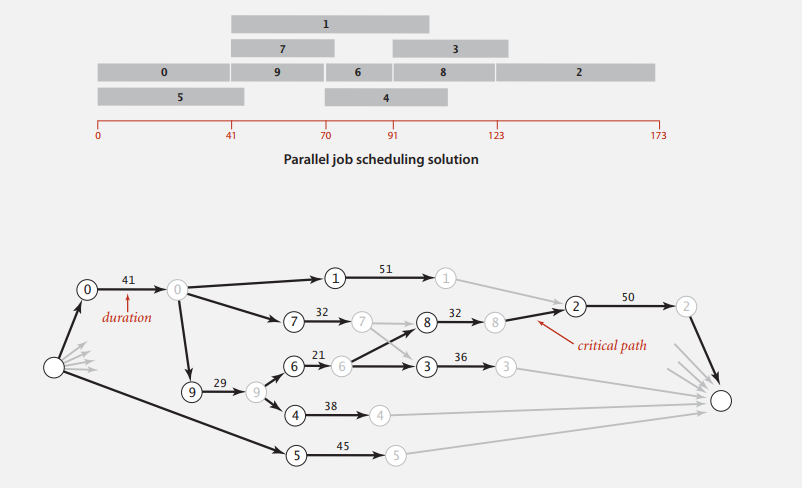
parallel-job-digraph

将任务调度抽象成带权无环有向图，每个任务预计开始时间即为从起点到它的起始顶点的最长距离，而图的最长路径 0->9->6->8->2 即并行任务调度问题的关键路径（完成所有任务的最早可能时间）。

Negative Weights

Dijkstra 算法不能处理负权重边，它会直接选择当前最短的边，而不会绕远路去走负权重的边。所以下图到点 3 的最短距离直接会是边 0->3 的权重 2，而不是实际上的 0->1->2->3 的总权重 1。

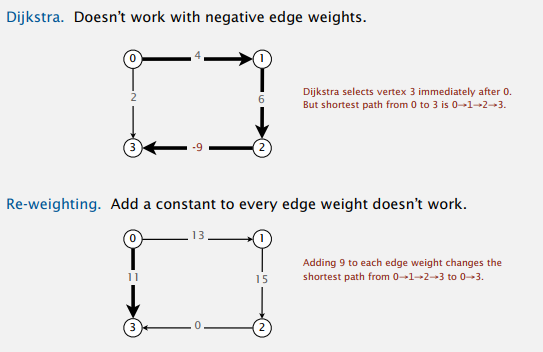
negative-edge-dijkstra

一个可能的尝试是把边权重都加上同一常数，让权重非负，但这样还是会改变最短路径，像上图那样。

介绍能处理负权重边的算法之前，要有个概念：当且仅当图不存在负权重环（环的总权重小于 0）时，SPT 存在。

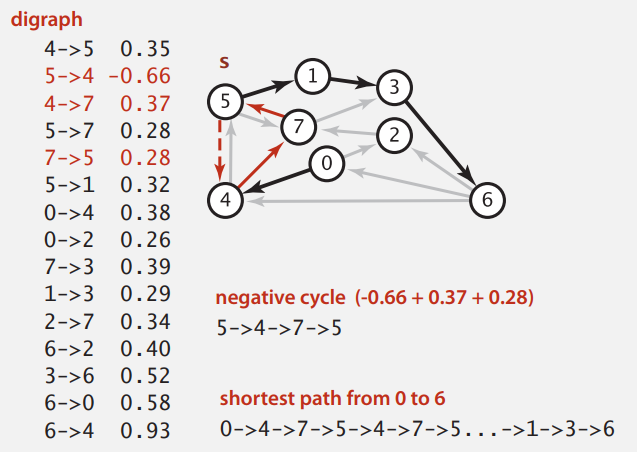
negative-cycle

存在负权重环，最短路径可能一直减少下去。

Bellman-Ford

算法步骤：

  1. 将 distTo[s] 初始化为 0，其它 distTo[] 元素初始化为无穷大。
  2. 重复 V 次：
    • 放松每条边。
for (int i = 0; i < G.V(); i++)
    for (int v = 0; v < G.V(); v++)
        for (DirectedEdge e : G.adj(v))
            relax(e);

Bellman-Ford 算法能够计算任意不含负权重环的带权有向图的 SPT，所需时间正比于 \(E \times V\)。

证明：

在没有负权重环的带权有向图中，对于源点 s 可到达的点 t，会存在最短路径，不妨记为：s=\(v_{0}\)->\(v_{1}\)->...->\(v_{k}\)=t，显然 k \(\leqslant\)V-1。证明算法正确性的等价命题：算法在第 i 轮之后能得到 s 到 \(v_{i}\) 的最短路径 \(v_{0}\)->\(v_{1}\)->...->\(v_{i}\)。

  • 对于 i=0，显然成立。

  • 假设算法在第 i 轮之后能得到 s 到 \(v_{i}\) 的最短路径，即为 distTo[\(v_{i}]\)。

  • 第 i+1 轮放松后，distTo[\(v_{i+1}\)]=distTo[\(v_{i}\)]+(\(v_{i}\)->\(v_{i+1}\)).weight()，因为：

    1. 每轮放松所有点，\(v_{i}\) 被放松后，distTo[\(v_{i+1}\)] 不会大于等式右边。
    2. 右边即最短路径 \(v_{0}\)->\(v_{1}\)->...->\(v_{i+1}\) 长度，也不会比它还小。

    所以在第 i+1 轮放松后，算法能够得到从 s 到 \(v_{i+1}\) 的最短路径。

改进：

如果 distTo[v] 在第 i 轮放松中没有改变，那么在第 i+1 轮中也就没有必要放松点 v。于是我们可以维护一个队列，保存 distTo[] 发生改变的那些点，下一轮只放松它们就好。为了防止重复放入，再来个布尔数组表示点是否已经在队列中。所以 Bellman-Ford 算法最坏情况下需要正比于 \(E \times V\) 的时间，但实际使用时一般会快很多。

Cost Summary

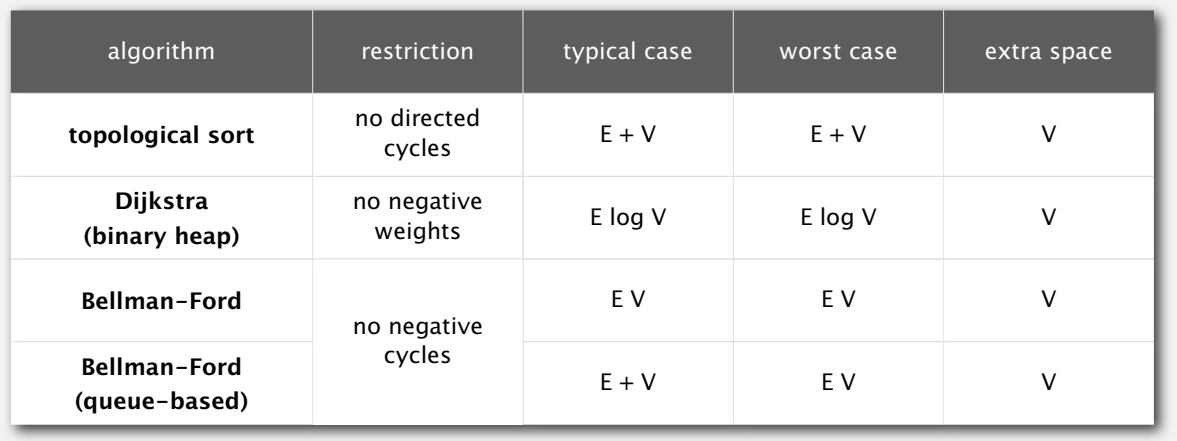
cost summary

Find A Negative Cycle

如果存在负权重环的话，基于队列实现的 Bellman-Ford 算法会陷入死循环，因为第 i 轮放松后找到的最短路径最多只有 i 条边，所以有必要实现检测负权重环的方法。

negative-cycle-api

如果图有负权重环，那么 edgeTo[] 还原出来的 SPT 就会有环，于是每一轮放松之后，就检测一下 SPT 是否有环。

private void findNegativeCycle() {
    int V = edgeTo.length;
    EdgeWeightedDigraph spt = new EdgeWeightedDigraph(V);
    for (int v = 0; v < V; v++)
        if (edgeTo[v] != null)
            spt.addEdge(edgeTo[v]);

    EdgeWeightedDirectedCycle cf = new EdgeWeightedDirectedCycle(spt);
    cycle = cf.cycle();
}

public boolean hasNegativeCycle() {
    return cycle != null;
}

public Iterable<Edge> negativeCycle() {
    return cycle;
}

实现用到了之前课程里检测环的类，详细的参见：BellmanFordSP.java，或是 booksite-4.4，不提。

Application

负权重环检测可以被应用于套汇。

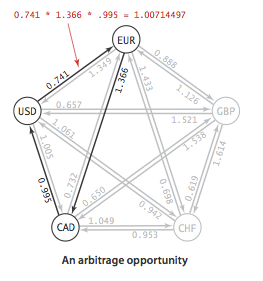
arbitrage

1000 美元可以换 741 欧元，后者再换成 1012.206 = 741 \(\times\) 1.366 加元，加元再换回美元变成 1012.206 \(\times\) 0.995 = 1007.14497，也就赚了 7.14497 美元。

在这样的图里寻找权重乘积（\(w_{1}w_{2}...w_{k}\)）大于 1 的路径，等价于 -ln(\(w_{1}\))-ln(\(w_{2}\))-...-ln(\(w_{k}\)) 小于零，于是我们把权重取对数再取反，找到的负权重环即目标路径。

posted @ 2018-06-22 18:53  archeroc  阅读(391)  评论(0)  编辑  收藏  举报