Minimum Spanning Trees
最小生成树
Introduction
图的生成树是它的一棵含有其所有顶点的无环连通子图。一幅加权无向图的最小生成树(MST)是它的一棵权值(树中所有边的权值之和)最小的生成树。
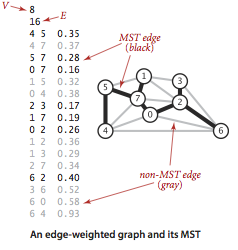
Greedy Algorithm
假定图是连通的,且各个边有不同的权值,这样图就会存在唯一一棵最小生成树。
Cut Property
切分将图的所有点分为两个非空且不重复的集合,横切边(crossing edge)指连接两个集合的边。
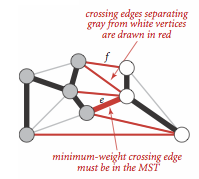
切分定理:在一幅加权图中,给定任意的切分,它的横切边中权重最小者必然属于图的最小生成树。
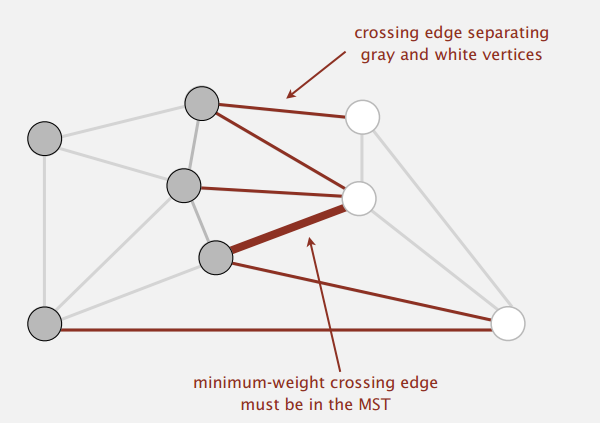
证明
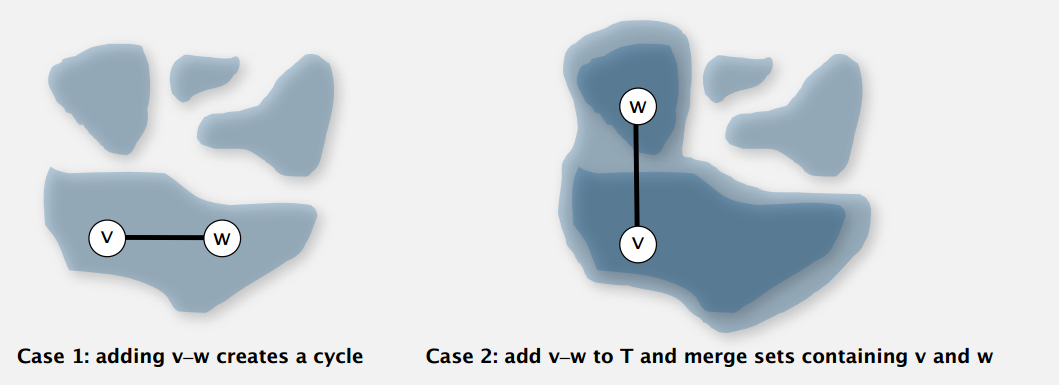
用反证法,假设图的最小生成树 T 不包含权重最小的横切边 e 。现将 e 加入 T ,则会产生一个包含 e 的环,而这个环必然至少含有另一条横切边 f 。又有 e < f ,此时我们删掉 f ,则可以得到一棵更小的生成树。矛盾。
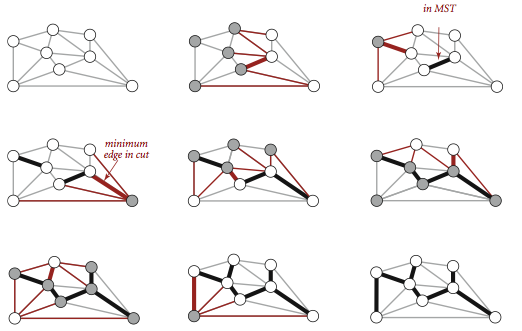
切分定理是解决最小生成树问题的所有算法的基础,这些算法都是一种贪心算法,每次选择一条权重最小的横切边,不断重复直到找到最小生成树的所有边,不同之处在于如何切分和判定权重。
Edge-Weighted Graph API
惯例先给出 API 再说具体要怎么实现。现在是加权图,需要给边新的表示。
Weighted Edge API

获取边 e 的两个端点:int v = e.either(), w = e.other(v),看下面的实现就能理解。
Weighted Edge: Java Implementation
public class Edge implements Comparable<Edge> {
private final int v, w;
private final double weight;
private Edge(int v, int w, double weight) {
this.v = v;
this.w = w;
this.weight = weight;
}
public int either() {
return v;
}
public int other(int vertex) {
if (vertex == v) {
return w;
} else {
return v;
}
}
public int compareTo(Edge that) {
if (this.weight < that.weight) {
return -1;
}
else if (this.weight > that.weight) {
return +1;
} else {
return 0;
}
}
}
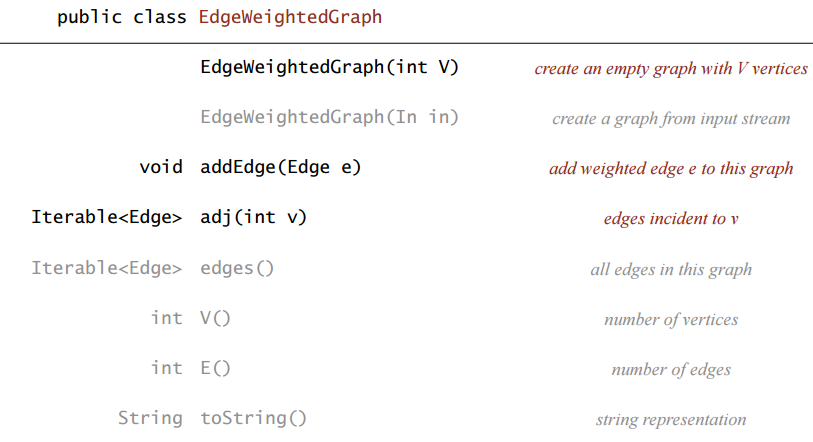
Edge-weighted Graph API
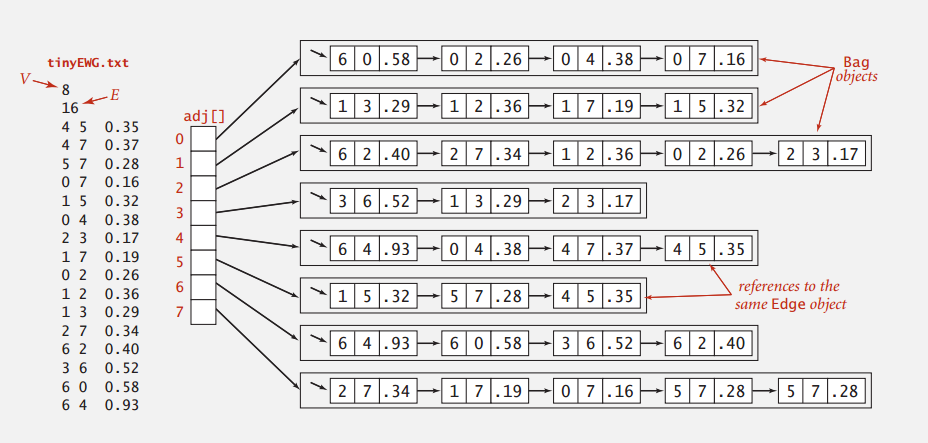
仍然使用邻接表来表示加权图,边的两个端点都有存指向边的引用,实际上表示边的对象只有一个。
Adjacency-lists Implementation
public class EdgeWeightedGraph {
private final int V;
private final Bag<Edge>[] adj;
public EdgeWeightedGraph(int V) {
this.V = V;
adj = (Bag<Edge>[]) new Bag[V];
for (int v = 0; v < V; v++) {
adj[v] = new Bag<Edge>();
}
public void addEdge(Edge e) {
int v = e.either();
int w = e.other(v);
adj[v].add(e);
adj[w].add(e);
}
public Iterable<Edge> adj(int v) {
return adj[v];
}
}
}
MST-API

Sample Client
public static void main(String[] args) {
In in = new In(Args[0]);
EdgeWeightedGraph G = new EdgeWeightedGraph(in);
MST mst = new MST(G);
for (Edge e : mst.edges()) {
StdOut.println(e);
}
Stdout.println("%.2f\n", mst.weight());
}
运行示例
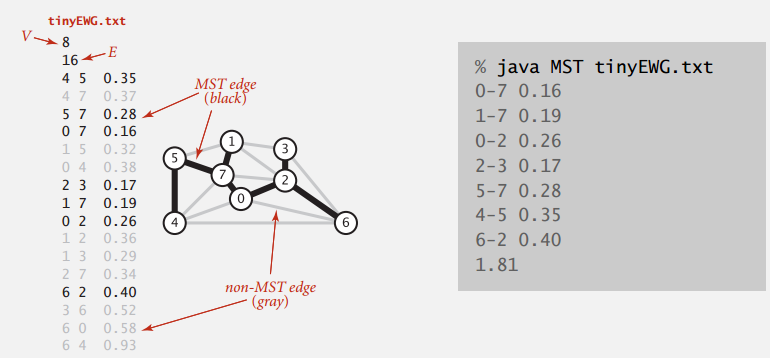
注:上面贴的大都不完整,完整的可以在 booksite-4.3 找到,图片也是。
Kruskal's Algorithm
Kruskal 算法很好说明,它先把所有的边按权重升序排列,然后从小到大把边加入最小生成树中,要求边不会和已经加入的边形成环(下图灰掉的就是会形成环的边)。
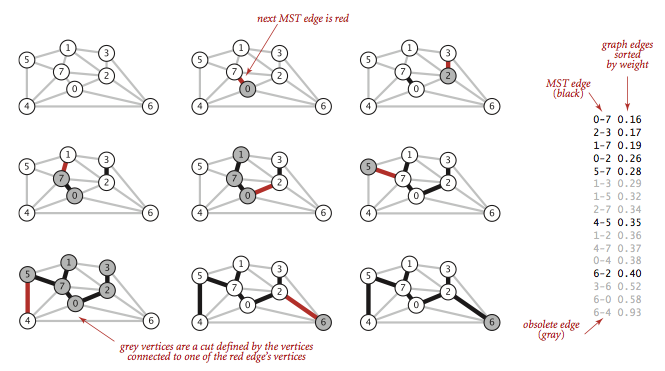
Kruskal 算法是上面提到的贪心算法的特例,MST 的点和图里其它的点构成一个切分,权重最小的横切边通过预排序和环检测得到,所以它可以计算任意加权无向图的 MST。
Kruskal: Implementation
用优先队列获取权重最小的边,用并查集来检测环,边的两点不在同一连通分量方可加入。
加权并查集加上路径压缩,检测环的均摊成本几乎是常数时间,时间复杂度来自优先队列的 \(ElogE\)。
public class KruskalMST {
private Queue<Edge> mst = new Queue<Edge>();
public KruskalMST(EdgeWeightedGraph G) {
MinPQ<Edge> pq = new MinPQ<Edge>();
for (Edge e : G.edges()) {
pq.insert(e);
}
UF uf = new UF(G.V());
while (!pq.isEmpty() && mst.size < G.V() - 1) {
Edge e = pq.delMin();
int v = e.eighter(), w = e.other(v);
if (!uf.vonnected(v, w)) {
uf.union(v, w);
mst.enqueue(e);
}
}
}
public Iterable<Edge> edges {
return mst;
}
}
Prim's Algorithm
Prim 算法也是贪心算法的特例,可以计算任意带权无向图的 MST。上一个算法贪心地每次尝试添加权重最小的边,把小树接起来最终接成 MST。Prim 算法从某一点开始,贪心地每次选择和树相连的权重最小的边来拓展,最终拓展成 MST。
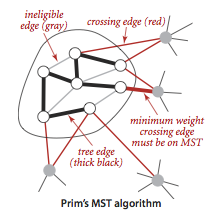
Prim 算法具体的实现有两种。
Lazy Implementation
“懒”实现不会删除优先队列里没用的边,以树的点为端点的边在拓展时都会被添加,所以拓展到后面就会出现两个端点都是树的点的无效边,“懒”实现的策略就是取出来发现无效就丢掉继续取下一个。
public class LazyPrimMST {
private boolean[] marked; // MST vertices
private Queue<Edge> mst; // MST edges
private MinPQ<Edge> pq; // PQ of edges
public LazyPrimMST(WeightedGraph G) {
pq = new MinPQ<Edge>();
mst = new Queue<Edge>();
marked = new boolean[G.V()];
visit(G, 0);
while (!pq.empty() && mst.size() < G.V() - 1) {
Edge e = pq.delMin();
int v = e.either(), w = e.other();
if (marked[v] && marked[w]) continue; // ignore if both endpoints in T
mst.enqueue(e);
if (!marked[v]) visit(G, v);
if (!marked[w]) visit(G, w);
}
}
// for each edge e = v-w,add to PQ if w not already in T
private void visit(WeightedGraph G, int v) {
marked[v] = true;
for (Edge e : G.adj(v)) {
if (!marked[e.other(v)]) {
pq.insert(e);
}
}
}
public Iterable<Edge> mst() {
return mst;
}
}
“懒”实现的瓶颈在优先队列,时间复杂度同样是 \(ElogE\) 级别。
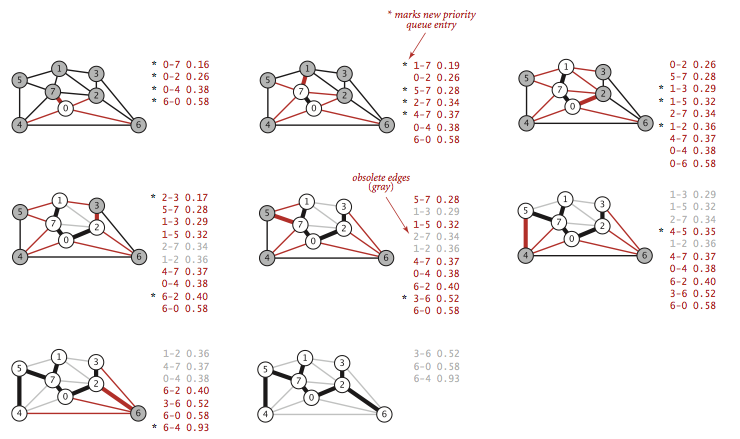
Eage Implementation
“即时”实现在优先队列里只保存必要的边,不存在两个端点都在树内的边,树外的点也只保留一条权重最小的连接树的边。下图灰掉的边,或是会形成环(如 1-2),或是现存端点到树权重更短的边(如 2-7)。
为了实现不存无用边的性质,对于给定的点,我们要能在优先队列中找出其到树目前的最短距离,看是否要更新。为此,需要用索引优先队列。我们把点当做索引,把点到 MST 的最小权重当做键值,来实现更新方法。
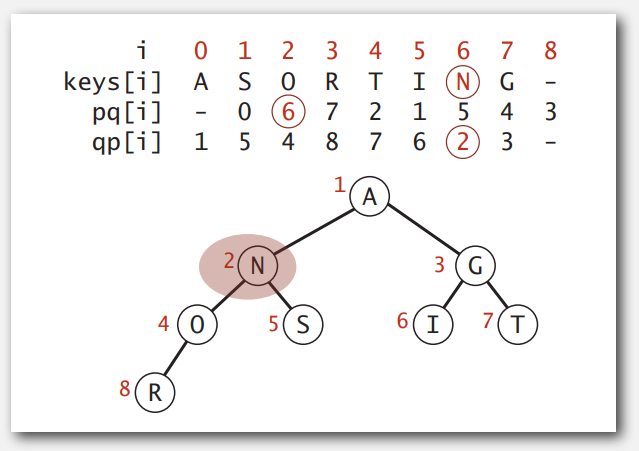
索引优先队列顾名思义,二叉堆数组里存放的是索引,孰大孰小由索引对应的键值决定。数组 keys 存放着键值,顺序无所谓;数组 pq 即二叉堆,下标 1 存放着最小键值对应的索引,最小键值即存放在 keys[pq[1]] 里。qp(queue position 吧)数组用于维护二叉堆,qp[i] 表示索引 i 在队列中的位置,即二叉堆数组的下标,元素则是索引,qp[] 则相反:下标对应索引,元素是位置,故有 qp[pq[i]] = i, pq[qp[i]] = i。
decreaseKey
public void decreaseKey(int i, Key key) {
keys[i] = key;
swim(qp[i]); // 键值变小,对应索引在二叉树中“上浮”
}
private void swim(int k) {
while (k > 1 && greater(k / 2, k)) {
exch(k, k / 2);
k = k / 2; // “上浮”一层
}
}
private boolean greater(int i, int j) {
return keys[pq[i]].compareTo(keys[pq[j]]) > 0;
}
private void exch(int i, int j) {
int swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
qp[pq[i]] = i;
qp[pq[j]] = j;
}
摘自 IndexMinPQ.java,还有很多其它方法,这里我们主要需要上述方法来更新权重。
Eager Code
public class PrimMST {
private Edge[] edgeTo;
private double[] distT;
private boolean[] marked;
private IndexMinPQ<double> pq;
public PrimMST(EdgeWeightedGraph G) {
edgeTo = new Edge[G.V()];
distTo = new double[G.V()];
marked = new bolean[G.V()];
for (int v = 0; v < G.V(); v++) {
distTo[v] = Double.POSITIVE_INFINITY;
}
pq = new IndexMinPQ<Double>(G.V());
distTo[0] = 0.0;
pq.insert(0, 0.0);
while (!qp.isEmpty()) {
visit(G, pq.delMin());
}
}
private void visit(EdgeWeightedGraph G, int v) {
marked[v] = true;
for (Edge e : G.adj(v)) {
int w = e.other(v);
if (marked[w]) continue;
if (e.weight() < distTo[w]) {
edgeTo[w] = e;
distTo[w] = e.weight();
if (pq.contains(w)) {
pq.decreaseKey(w, distTo[w]);
}
esle {
pq.insert(w, distTo[w]);
}
}
}
}
}
完整的参见:PrimMST.java。
“即时”实现的优先队列没有那么多无用的边,拓展到的每个点只有一条当前最优的边,最多只会有 V 条边,故所需空间和 V 成正比,时间复杂度为 \(ElogV\) 级别。
Context
回顾了 MST 问题的发展,不提。目前还没找到线性的算法,也没有理论能证明线性算法不存在。但总的来说,可以认为在实际应用中 MST 问题已经被解决了,大多数图只要花比遍历所有边多一点的成本。


