AES的简要原理和参考实现
产生背景:高级加密标准AES(Advanced Encryption Standard)是在DES受到不断攻击威胁的背景下推出的。1997年4月15日,美国国家标准技术研究所(NIST)向全世界征集高级加密标准算法(主要指标:(1)安全性,(2)成本,(3)算法和实现特性等)。有5个候选算法进入了最后一轮评选,分别是:MARS,RC6,Rijndael,Serpent和Twofish,最终获胜的Rijndael算法即为目前通称的AES算法。
Rijndael由两位比利时密码学家Vincent Rijmen和Joan Daemen设计,具有良好的有限域以及有限环数学理论基础(只会简要介绍)。Rijndael算法属于分组加密算法,分组长度可以是128比特、192比特和256比特,密钥长度也是这三个可选值。不同的分组组合,迭代次数和密钥拓展时略有差异,只介绍AES-128版本的加密部分。
数学基础:字节运算是Rijndael的基本运算,一个字节可以用\(GF(2^8 )\)中的元素表示。有限域\(GF(2^8 )\)的运算可以采用几种不同方法表示,Rijndael算法选择传统的多项式表示。将\(b_7 b_6 b_5 b_4 b_3 b_2 b_1 b_0\)构成的字节b看成系数在{0,1}中的多项式:\(b_7 x^7+b_6 x^6+b_5 x^5+b_4 x^4+b_3 x^3+b_2 x^2+b_1 x+b_0\),例如十六进制数‘57’对应的二进制为01010111,看成一个字节,对应的多项式为\(x^6+x^4+x^2+x+1\)。
在多项式表示中,两个元素的和仍然是一个次数不超过7的多项式,其系数等于两个元素对应系数的模2加(按位异或)。由于每个元素的加法逆元等于自己,所以减法和加法相同。
在\(GF(2^8 )\)上的乘法定义为二进制多项式的乘积以8次不可约多项式\(m(x)=x^8+x^4+x^3+x+1\)(十六进制表示为'11B')为模约减的结果。例如十六进制的'80'⋅'02'='1B':
\('80'⋅'02'=(1000 0000)_2⋅(0000 0010)_2\)
\(=x^7⋅x=x^8+(x^8+x^4+x^3+x+1)(mod m(x))\)
\(=x^4+x^3+x+1=(0001 0000)_2='1B'\)
\(GF(2^8 )\)上还定义了一个运算,称之为x乘法,其定义为:\(x⋅b(x)=b_7 x^8+b_6 x^7+b_5 x^6+b_4 x^5+b_3 x^4+b_2 x^3+b_1 x^2+b_0 x(mod m(x))\)。如果\(b_7=0\)的话,则乘积结果求模后不变,反之乘积结果求模则会减去m(x)(即异或)。于是,当x(十六进制数'02')与b(x)相乘时,可以先将b(x)在字节内左移一位(最后一位补0),若\(b_7=1\),则再和'1B'(其二进制为00011011,因为要模\(m(x)=x^8+x^4+x^3+x+1\))做逐比特异或来实现。乘法运算满足分配律,可以将复杂的乘法运算分解成'01'和'02'的乘法组合来简化计算。
AES:高级加密标准AES(Advanced Encryption Standard)的明文及中间处理结果(迭代各轮的输入、输出)都称为状态,且被表示成4行的矩阵,矩阵的每个元素是一个字节,并看成是\(GF(2^8 )\)上的一个元素。把一个明文分组写成矩阵时,按先列后行的规则写入。对于AES-128来说,明文和密钥都是4×4的矩阵。AES的加解密原理框图如下:
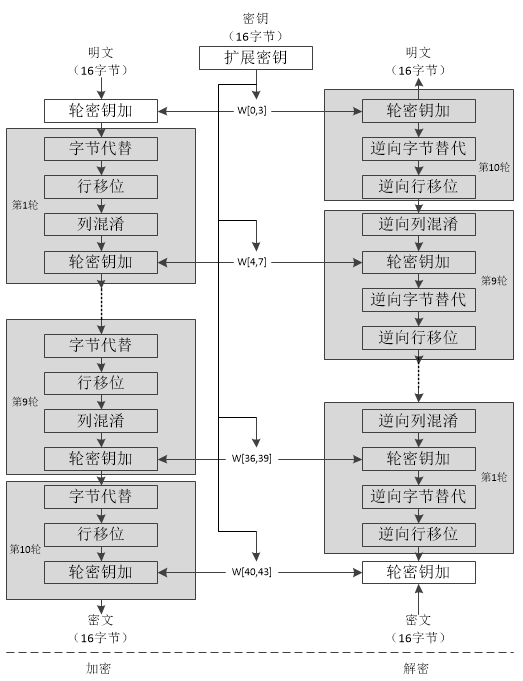
AES-128算法由10轮组成,加解密过程满足可逆性。AES-128加密过程如下:1. 初始变换之轮密钥加。明文状态数组与第一个轮密钥进行加法运算。轮密钥被表示成与明文状态同样大小的矩阵,由种子密钥通过密钥扩展算法产生。2. 完全相同的9轮迭代。每轮以此执行字节替换、行移位、列混合和轮密钥加。每一轮以上一轮的输出为输入。3. 结尾轮变换。与前面各轮稍有不同,依次执行字节替换、行移位和轮密钥加。取消了列混合。执行完结尾轮后的状态按先列后行输出就是密文。
字节替换(ByteSub)是一个关于字节的非线性变换,具体的数学结构比较复杂,不展开描述。实现的时候,使用一个事先构造好的16×16的S盒来完成替换,S盒替换表如下:
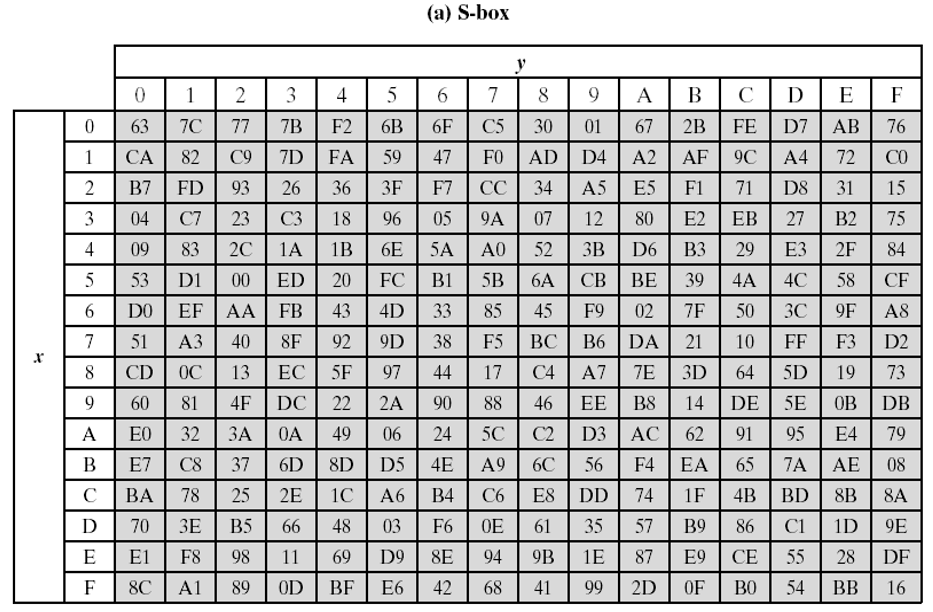
这个S盒完成一个8比特输入到8比特输出的映射,比如说输入的字节是\((CB)_16=(11001011)_2\),S盒中第C行第B列交叉处的值(1F)即为替换的输出。
行移位变换(ShiftRow)是将状态阵列的各行进行循环移位,不同状态行的位移量不同,下图展示的是128位版本的移位情况:
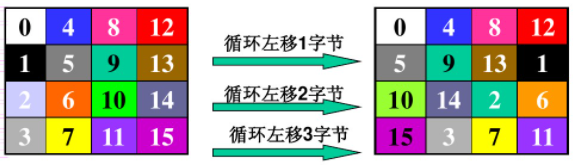
列混合变换(MixColumn)是将状态阵列的每个列视为系数在\(GF(2^8)\)上、次数小于4的多项式,再与同一个固定的多项式c(x)进行模\(x^4+1\)乘法运算。AES设计者给出的\(c(x) ='03' x^3 +'01' x^2 + '01' x+'02'\),背后的数学原理略过,写成矩阵形式如下:
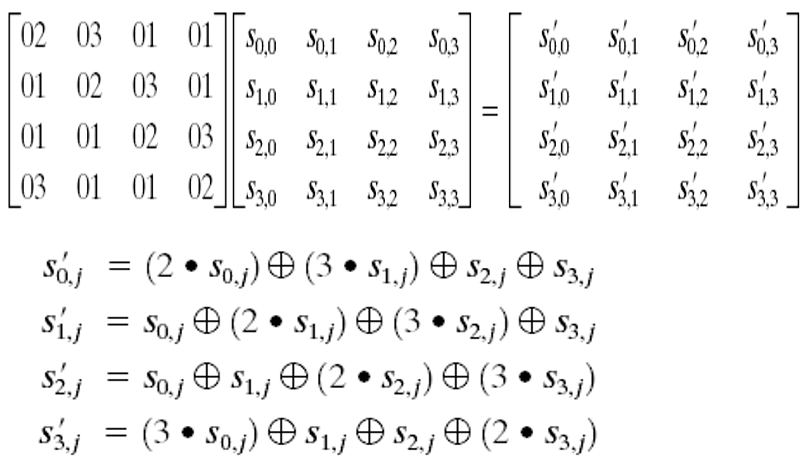
上面已经是按模\(x^4+1\)计算后的结果,至于里面的乘法运算则还是之前数学基础中定义的\(x^8+x^4+x^3+x+1\)。另外,所乘因子都是比较简单的,乘\((01)_{16}\)还是不变,乘\((02)_{16}\)即前面介绍的x乘法,而\((03)_{16} \cdot s=(02)_{16} \cdot s \oplus s\)。
轮密钥加变换(AddRoundKey)是轮密钥阵列简单地与状态阵列做矩阵加法运算,定义在\(GF(2^8)\)上的加即为两个字节逐比特异或。轮密钥阵列由密钥拓展算法得到。
密钥拓展是AES密码算法的一个重要组成部分,原理示意图如下:
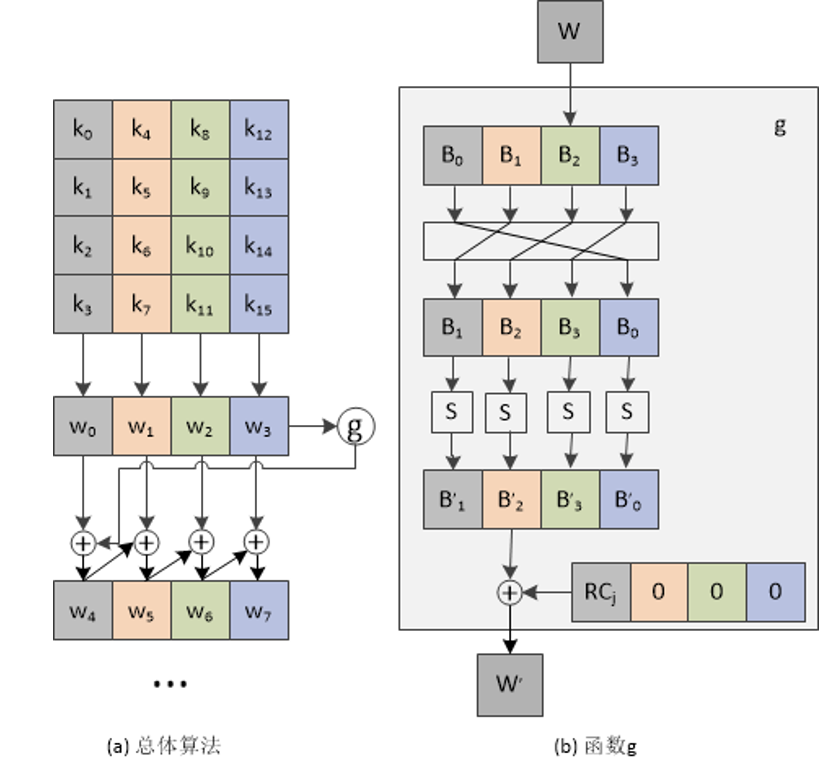
将密钥矩阵每列四个字节看做一个元素,即上图中的\(w_0\),\(w_1\),\(w_2\)和\(w_3\),对于输出的子密钥\(w_j (j∈[4,43])\),定义为:
至于函数g,会先把输入的w循环左移8位,再对每个字节做S盒替换,最后与32比特的常量(RC[j/4], 0, 0, 0)进行异或。RC是一个一维数组:[0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36]。RC的值只需要有10个,而此处用了11个,实际上RC[0]在运算中没有用到,增加是为了便于程序中用数组表示。由于j的最小取值是4,j/4的最小取值则是1,因此不会产生错误。
参考实现:python
参考资料:

