3DES的简要原理和参考实现
3DES
分组密码:对于明文编码后的二进制序列，分组密码会将其划分成长度固定的组（块），每组分别在密钥的控制下转换成等长的密文分组。分组密码算法的安全策略中，用得最多的就是采用代换-置换网络（Substitution-Permutation Network），简称S-P网络，是由S变化（代换）和P变化（置换或换位）交替进行多次迭代而形成的变换网络。
Feistel结构：通过代换和置换（S-P网络）交替的方式来构造分组密码，该结构是可逆的，也可以用来解密，结构示意图如下：
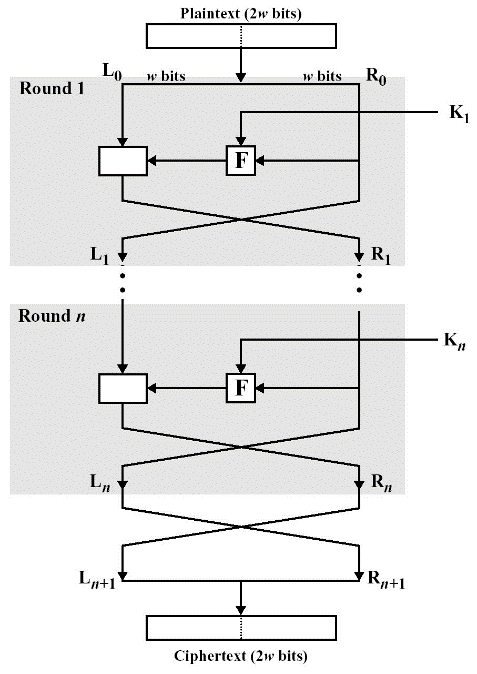
加密算法输入的是一个长度为2w比特的明文分组和一个密钥K，明文分组被分成左右两个部分\(L_0\)和\(R_0\)，数据的这两个部分经过n轮的处理之后组合起来产生密文分组。第i轮将以第i-1轮的运算结果\(L_{i-1}\)和\(R_{i-1}\)作为输入，在对应的子密钥\(K_i\)下，进行密码转换。一般地，\(K_i\)由主密钥（初始密钥）K输入到密钥拓展算法来产生。在Feistel网络中，n轮结构都一样，第i轮加密变化可用数学表达式描述如下：
其中函数F被称作轮函数，一般包含代换和置换，起混乱和扩散的作用。因此，设计一个良好的非线性轮函数，对算法的安全性来说是很重要的。轮函数的输出再和左半部分异或，得到下一轮的右半部分的输入。
当Feistel结构用于解密时，第一轮的输入是加密第n轮的输出（密文），第j轮的输入时加密过程第n-j+1轮的输出，第n轮的输入是加密过程第1轮的输出，第n轮的输出就是加密过程第1轮的输入，即明文。解密变化可用数学表达式描述如下：
DES：采用Feistel结构，密钥长度为64位，实际只使用56位（另外8位为奇偶校验位），明文和密文的长度都是64位。简化的示意图如下：
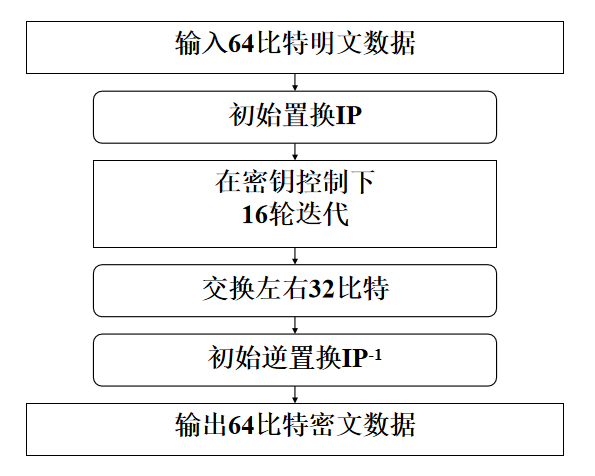
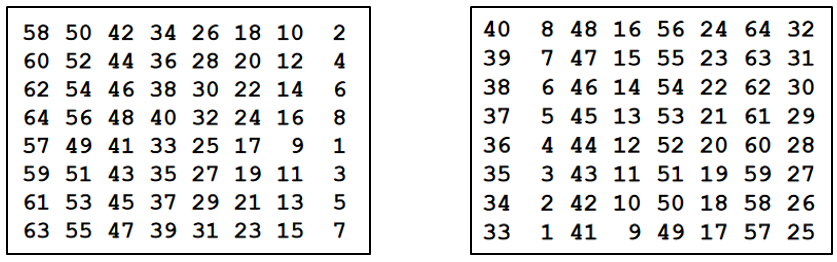
初始置换IP对明文的64位进行换位处理，然后通过子密钥对明文进行16轮乘积变换，最后经过逆初始置换的处理，得到64位密文输出。算法的开始和结束增加置换操作，可以增加算法的抗分析能力。初始置换IP表如下左图。其含义为：明文中第58位变为第1位，明文中第50位变为第2位，…，明文中第1位变为第40位，…，明文中第7位变为第64位。逆初始置换则相反，再把顺序调回去，像第40位变为第1位，表如下右图。
16轮迭代过程即使用前文的Feistel结构，每一轮变化的核心F函数包含三个子过程：扩展置换，S盒替换（压缩）和P盒置换，将32位的输入变为32位的输出，结构如下左图。扩展置换简称E函数（Expand），功能是把32位扩展成48位，是一个与密钥无关的变换。扩展置换按32位输入，分为8组，每组4位，经E函数扩展后变成每组6位输出。E函数如下右图，第一位输入将会位于后续的第1和第8子分组中，这样明文或密钥的一点小变动，可以使密文产生较大变化。
扩展结果与子密钥进行异或运算，结果作为S盒的输入。压缩替换（S盒）通过8个S盒将48位输入变换为32位输出，结构如下图。
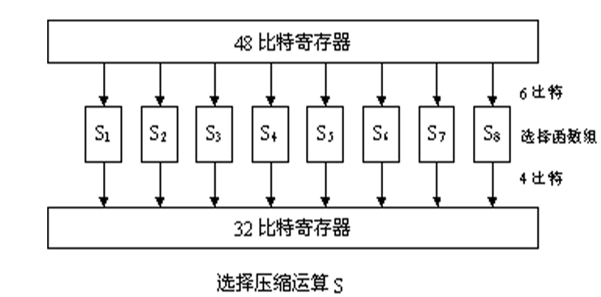
每个S盒都有4行16列，对于输入的6个比特，第1和第6比特组成二进制的行号，第2到第5比特组成二进制的列号，由此确定的S盒的位置上的10进制数的4位二进制数即为输出。举例来说，输入101001，行号11，列号0100，即第3行第4列。如果是S2的话，对应位置为3，输出即为0011。
最后的P盒置换和前文的初始置换IP类似，会将S盒压缩替换得到的32位结构重新排列顺序，这就是F函数的最终输出了，排列顺序表就不贴了。
现在还有一个问题是怎么生成子密钥，生成子密钥的过程示意图如下：
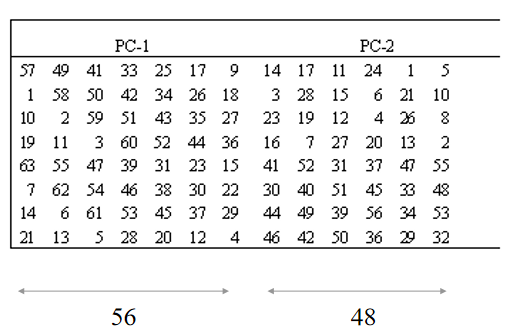
64位初始密钥中，只有56位是密钥，剩下8位是奇偶校验位（分布在8，16，24，32，40，48，56，64比特位置上）。子密钥的生成大致有三个过程：置换选择1，循环左移，置换选择2，分别产生16个子密钥。置换选择1和前文P盒类似，打乱顺序，还去掉密钥中的奇偶校验位。循环左移之前，前后28位各分成一组。循环左移的位置每一轮可能不同，在第1，2，9，16时，左移一个位置，其余左移两个位置。置换选择2也有一个表，用于从56位密钥比特串中置换后送出48位比特。置换选择1和置换选择2的表分别如下的左图和右图。
DES使用了Feistel结构，解密可以使用同一个算法，所不同的是子密钥的使用顺序相反。但是，DES也存在一些问题，比如说56位的密钥提供的安全性日益下降，S盒的设计原理未公开，可能隐含有陷阱等。现代常规分组加密算法中，一种是对DES进行复合，强化抗攻击能力；另一种是开辟新方法。
中间相遇攻击：对于双重DES来说，有\(C=E_{K2} (E_{K1} (P))\)（其中C指密文，P指明文，E指加密，D指解密，K指密钥），于是存在\(X=E_{K1} (P)=D_{K2} (C)\)。
假设已知一个明文密文对(P, C)，则可以先用\(K_1\)所有可能的\(2^{56}\)个密钥加密P，并对结果按X的值排序保存。再遍历\(K_2\)所有可能的\(2^{56}\)个密钥解密C，如果有\(K_1\)，\(K_2\)使得\(E_{K1} (P)=D_{K2} (C)\)成立，那么这两个密钥就有可能是正确的密钥。而如果已知两个明密文对的话，可能的概率可以达到\(1-2^{-16}\)。而且，中间相遇攻击的代价（加密或解密所用运算次数）\(≤2×2^{56}\)，比攻击单DES所需的\(2^{55}\)多不了多少。
因为二重DES的密钥长度理论上为112位，而64位的明文加密成64位的密文只有\(2^{64}\)种可能，所以一个明文到密文的变化对应着\(2^{112}/2^{64}=2^{48}\)种可能的密钥。另一方面，对第一个明密文对成立的密钥，使第二个明密文对成立的概率为\(1/2^{64}\)。那如果知道两个明密文对，虚警率则降为\(2^{48-64}=2^{-16}\)，或者说中间相遇攻击的成功率为\(1-2^{-16}\)。
3DES：由于2DES和4DES易受中间相遇攻击的威胁，实用中一般广泛采用的主要是三重DES方案，有四种使用模式，即：
- DES-EEE3模式。使用三个不同密钥\((k_1,k_2,k_3)\)，采用三次加密算法。
- DES-EDE3模式。使用三个不同密钥\((k_1,k_2,k_3)\)，采用加密-解密-加密算法。
- DES-EEE2模式。使用两个不同密钥\((k_1=k_3,k_2)\)，采用三次加密算法。
- DES-EDE2模式。使用两个不同密钥\((k_1=k_3,k_2)\)，采用加密-解密-加密算法。
前两种的总密钥长度达到了168位，后两种的总密钥长度为112位，有效克服了DES面临的穷举搜索攻击，也增强了抗差分分析和线性分析的能力。
参考实现：python
参考资料:
