Geometric Search
几何搜索
平衡搜索树(BST)在几何方面的应用,处理的内容变成几何对象,像点,矩形。
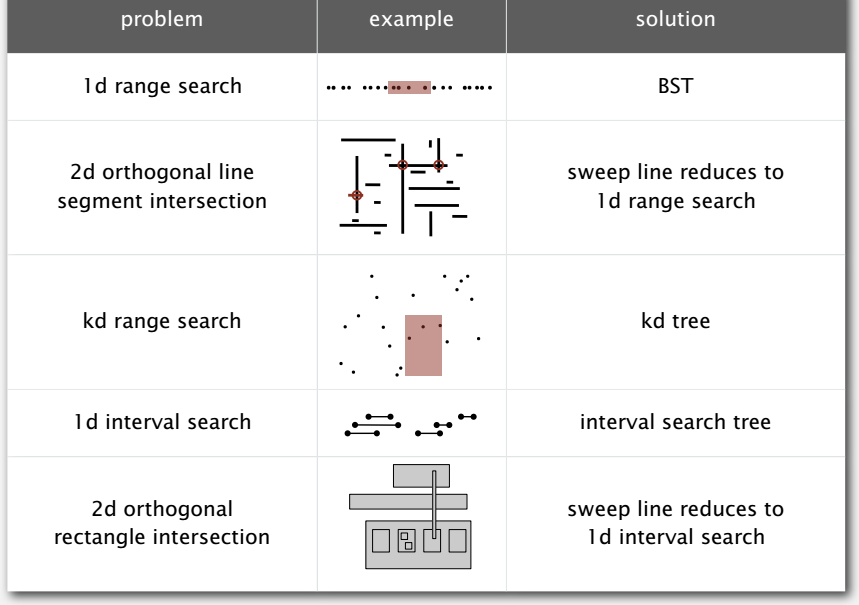
1d range search
先来看一维的情况,一维的范围搜索是后面的基础,处理的对象是在一条线上的点。这是符号表的一个小拓展,多了范围查找(range search) 和范围计数(range count)即希望知道给定范围上有哪些点或是有多少点。
用无序链表来实现的话,插入直接放开头,但是范围查找和范围计数都需要正比于 N 的时间。用有序数组来实现的话,范围计数的时间复杂度是 logN 级别,范围查找是 R+logN 级别(范围内有 R 个点),插入为了维护有序性需要的时间也和 N 成正比。所以说,高效的实现得用 BSTs,插入和范围计数的时间复杂度都是 logN,范围查找的则是 R+logN。
范围计数:
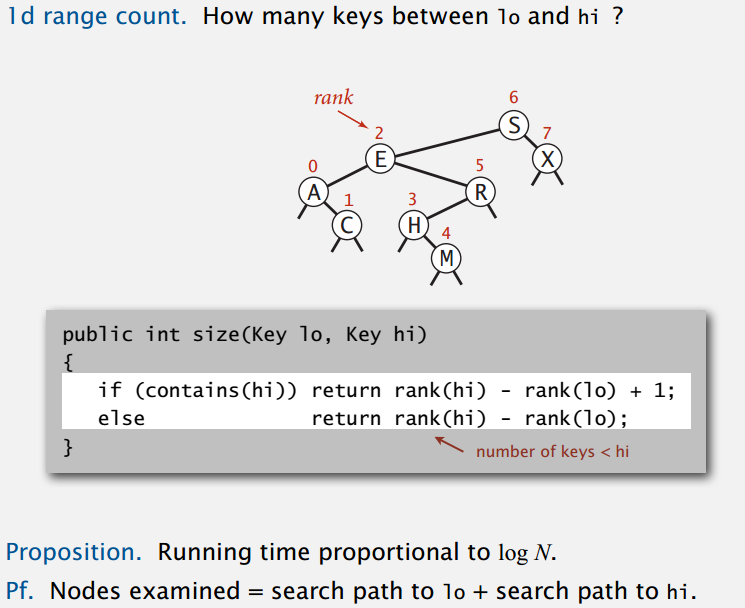
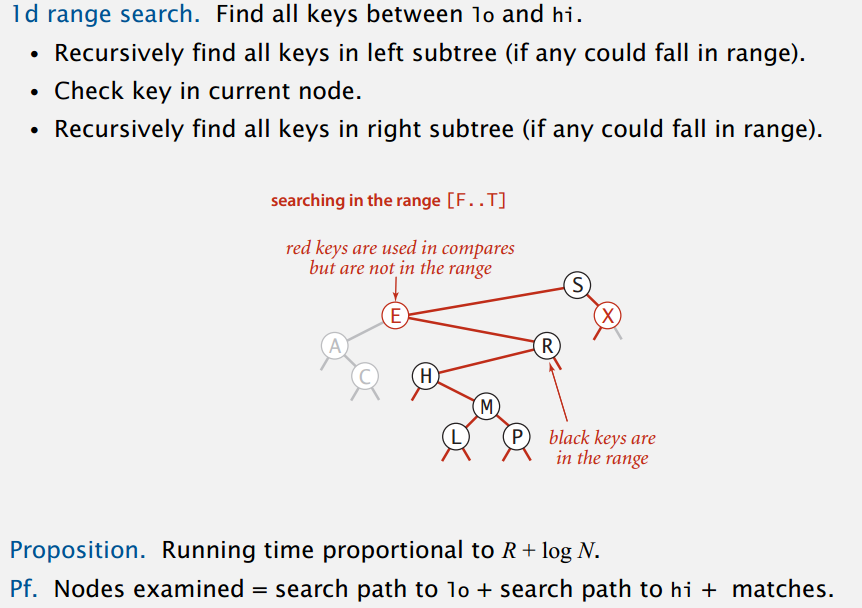
范围查找:
line segment intersection
接着我们到二维,设想有很多水平或垂直的线段,现在希望找到所有交点。
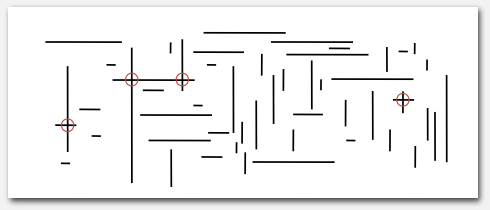
遍历检查所有可能组合会是平方级别的复杂度,显然是不可接受的,其实我们可以把问题转成上面一维的情况。
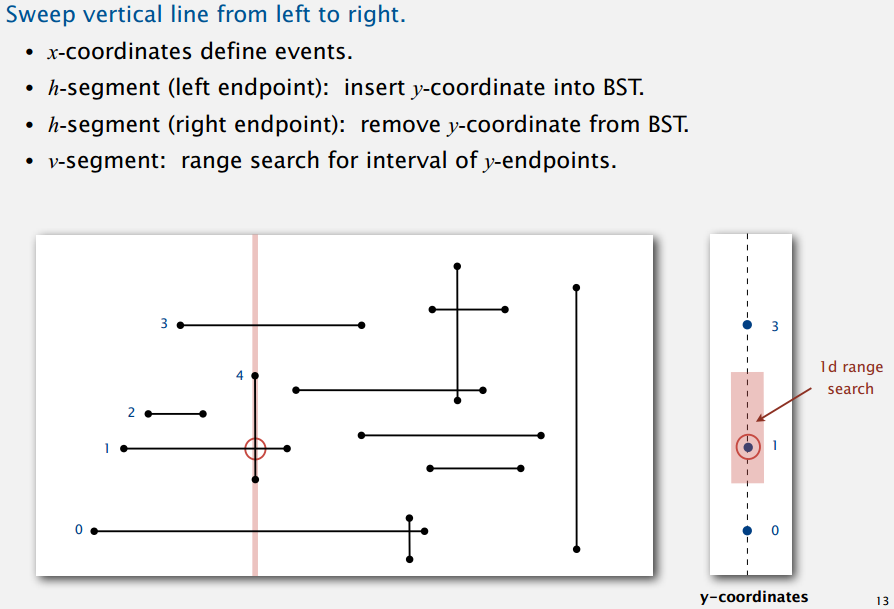
方便起见,这边的线段没有重合啥七七八八的情况。假想有一条垂直的线,从左扫到右,碰到水平线段的左端点就把该线段的 y 值放入 BST,碰到水平线段的右端点就把该线段的 y 值从 BST 中移除,碰到垂直线段就以该线段的上下端点为区间在 BST 中做范围计数。像上面的例图,点 2 已经从 BST 中移除了,点 4 是第一个垂直线段,范围查找发现有个点 1,也就发现了第一个交点。
kd trees
kd 树是 BSTs 的拓展(k 个维度),可以高效地处理空间中的点,十分灵活,在很多应用中很有用。就算不是几何问题,在数据库中你可能想知道收入在 1m - 10m 且年龄在 40 - 50 岁的人有哪些,这种场景也好用。
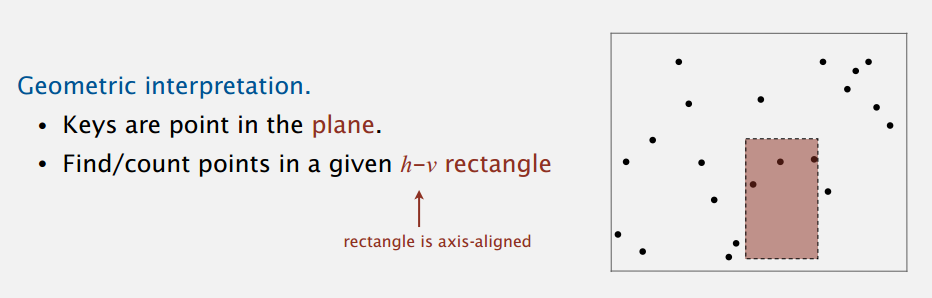
现在的例子正式从一维拓展到二维,范围查找和范围计数从区间上升到矩形,即希望知道平面上有哪些点或是有多少点在查询的矩形上。
一个可能的做法是把平面用网格划分,比较理想状况下是这样的:
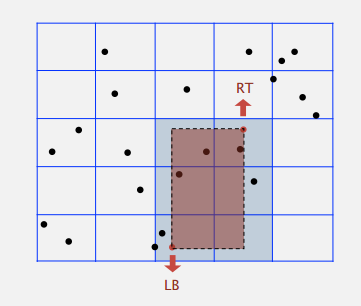
点的分布比较均匀,每个网格可以对应一个链表来表示在其中的点。范围查找的时候就检查涉及到的网格,不用遍历整个平面,从而提高搜索效率。
M * M 的网格,M 太大会浪费空间,太小每个网格会有好多点,N 个点可以考虑设为 \(\sqrt []{N}\)。但是吧,对于几何数据,聚集(clustering)是一个很常见的现象,没法均匀地分布在网格上,比如像下面的地图数据:
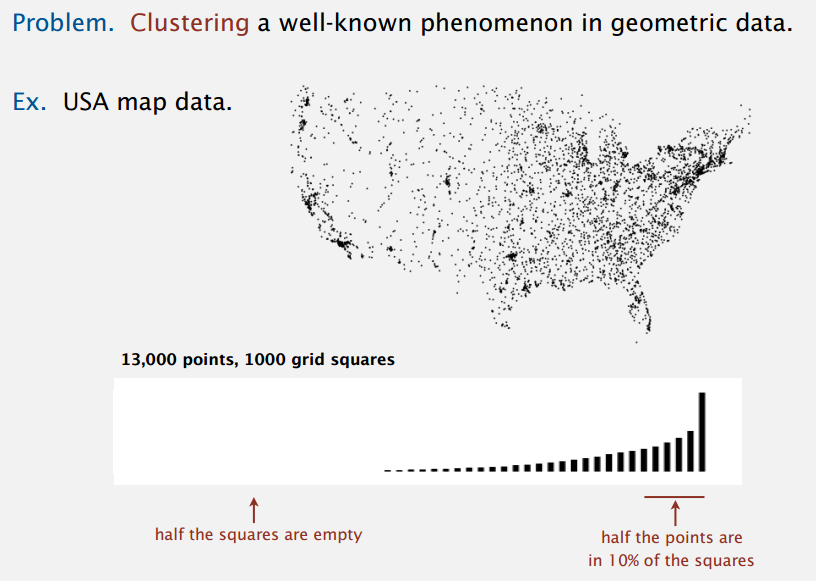
所以说,网格划分不大适合我们的应用场景,经常会有好多点在一格,不然开好多小格又会浪费空间。但是,空间划分的想法是好的,我们可以用树结构类似的递归把空间分成两半两半。
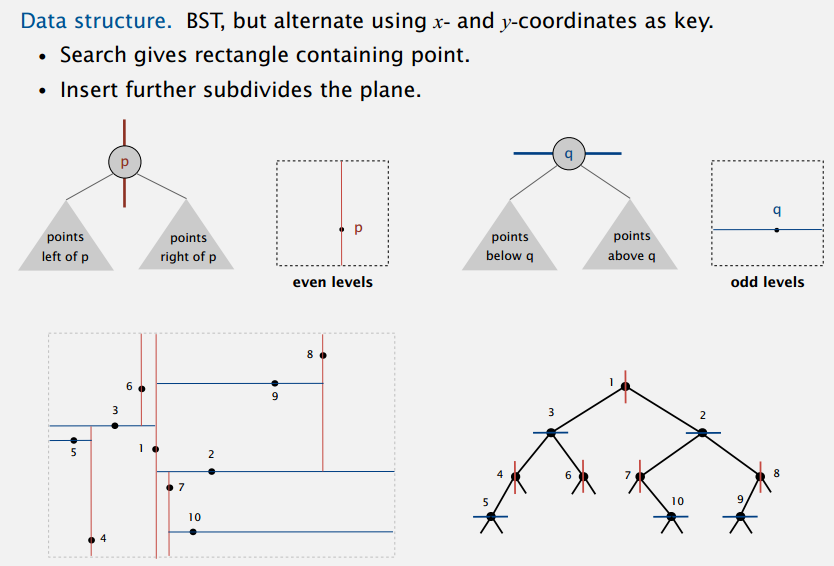
树节点的键交替用 x,y 坐标,左右孩子还是原来那样一个小一个大,在平面上来看就是点的上下或左右。
应用方面,举了范围查找和搜索最近邻居两个例子。
range search in a 2d tree
在 x 节点比较横坐标选左右,在 y 节点比较纵坐标选择上下,就是二分吧,一次砍掉一半搜索空间。
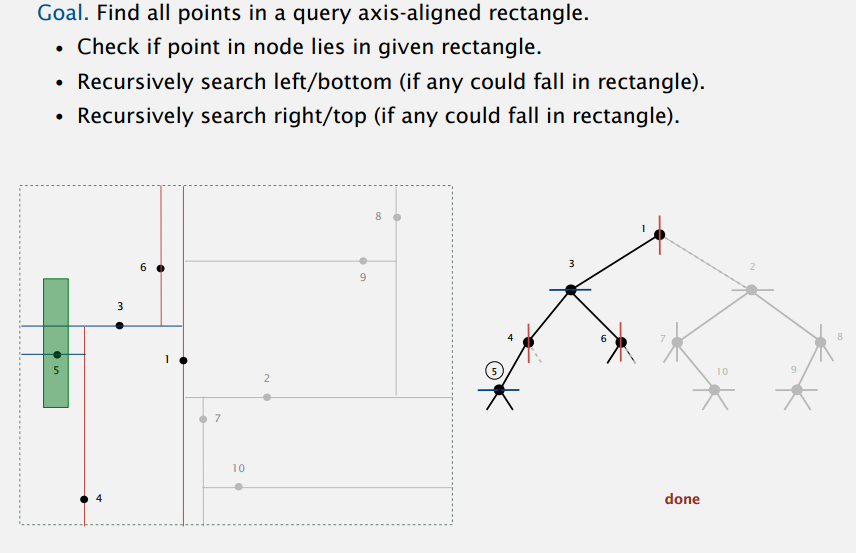
第一次点 1 不在查询矩形里,接着发现矩形在左边,右子树马上整个不要;接着点 1 的左孩子点 3 也不在矩形里,但 y 坐标在区间里所以上下都要搜索;点 4 和点 1 一样,只要搜索左边;现在找到点 5 在矩形里,两个孩子为空结束搜索;继续返回搜索点 3 的另一边,点 6 也只要搜索左边,为空结束,至此完成整个搜索过程。
典型情况下,2d 树的时间复杂度为 R+logN (R 是在矩形中的点的个数),但是吧,最坏情况下,即使树是平衡的,复杂度也是 \(R+\sqrt []{N}\) (课程说相关证明超纲不提)。可是,对于很多实际应用来说,2d 树易于实现而且也值得一用。
nearest neighbor search in a 2d tree
搜索过程类似,每次选择查询点所在的一边,虽然最近的点也可能在另外一边,但是一般来说在同一边的概率大,所以这里采取这样的选择。
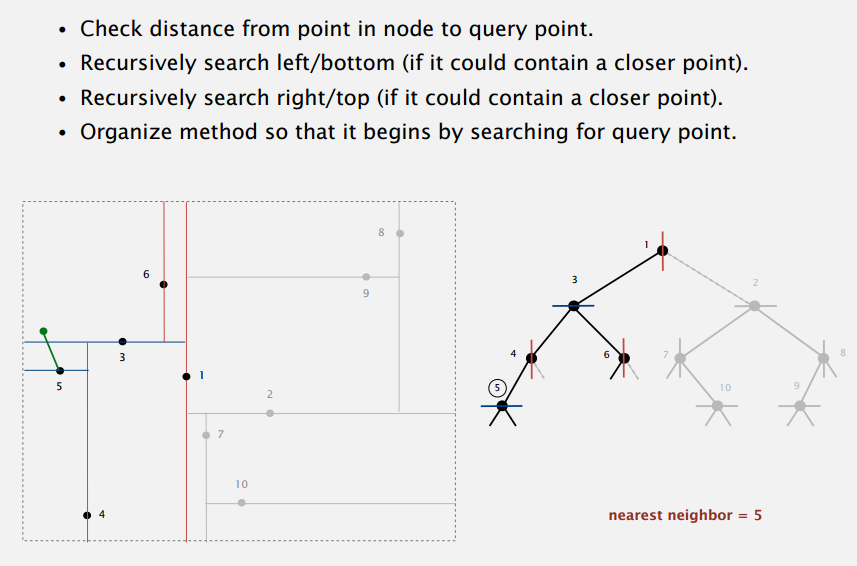
一路找下来,更新离查询点最近的距离和点。找到点 5 之后返回搜索点 4 的右边,为空继续返回搜索点 6 的右边,同样为空到了点 1 的右边。这里应该也可以有是否剪枝的判断,好像这次的编程作业就有这个,比如说现在点 5 到查询点的距离明显小于查询点到点 1 所在垂直红线的距离,那么点 1 的右子树就完全可以砍掉。
性能方面,典型情况是 logN,最坏情况是 N,我想了下,比如说点在圆上,然后查询点在圆心这样子。反正,一般来说,还是很高效的。
interval search trees
原来一维上的研究对象是点,现在再来看看一维下的区间(线段),问题是查找和给定区间有交集的区间。

还是用 BST 来表示,区间左端点为键(这里假定没有重复的左端点),同时在节点里保存后代最大的右端点。
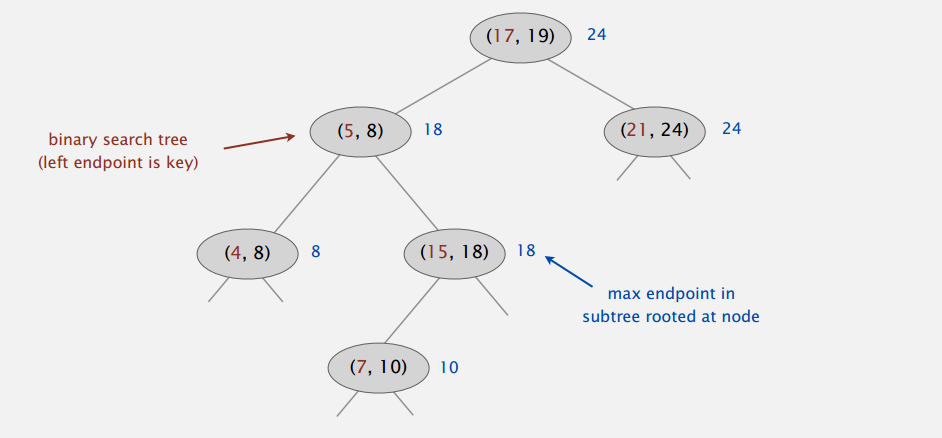
插入新的节点的时候,通过比较左端点来找到合适位置,然后看看路径上最大右端点是否要更新。
查找的时候,节点有交集就直接返回(先说找到任一相交区间),不然就把查询区间左端点和左孩子的最大右端点比较,前者比较大就可以砍掉左子树;后者比较大就需要查找左子树。要注意的是,第二种情况下,左子树可能还是没有相交的区间,然后!这个时候的右子树也是不用搜索的。

要是查询区间在左子树没有相交区间,右端点最大的那个区间的左端点 c 肯定在前面,而右子树的左端点又比左子树的大,所以就像上图那样可以不用找右边了。
实现上,可以用红黑树来保证对数级别的性能,找到所有相交区间的复杂度是 RlogN,就一共有 R 个相交的区间这样。
retangle intersection
最后,把二维下的处理对象也升级为矩形,希望知道平面上矩形相交的个数。课程说这个有实际的需求,大概是用来检查电路板之类的,因为摩尔定律啊,平方级别的算法肯定是不行的。
算法和检查二维线段相交差不多,然后这边假定 x,y 坐标不重复。

类似的变成一维上的区间相交检测,在 N 个矩形查找 R 个相交的复杂度是 NlogN + RlogN。
最后的最后,贴张归纳: