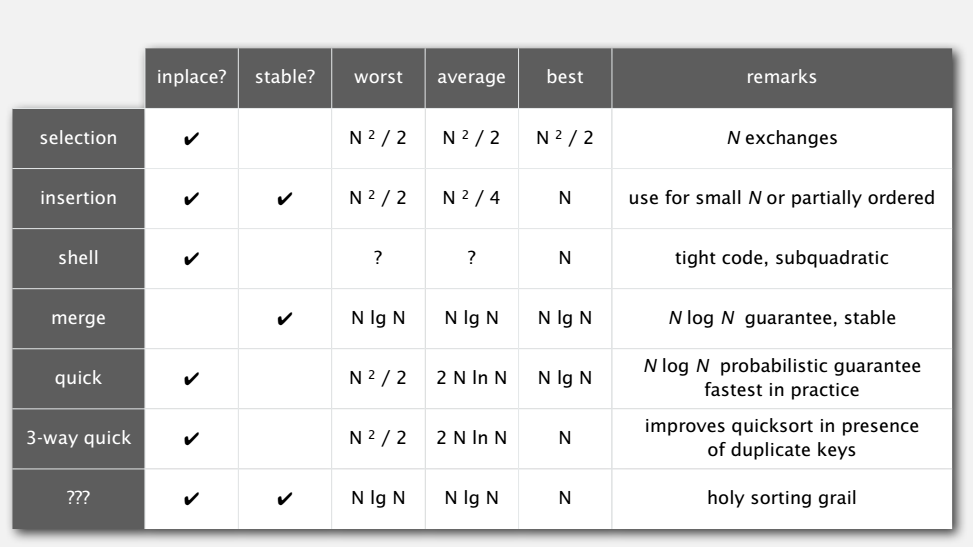
Quicksort

快排

快排是另一个经典的排序算法，在实际中也被广泛地应用。

quicksort

快排的基本思想：

• 混洗（shuffle）打乱待排数组。

• 这样划分（partition）数组：

  • 元素 a[j] 在排好的位置上。
  • j 左边元素都不大于 a[j]。
  • j 右边元素都不小于 a[j]。

• 递归地排好 j 的左边和右边。

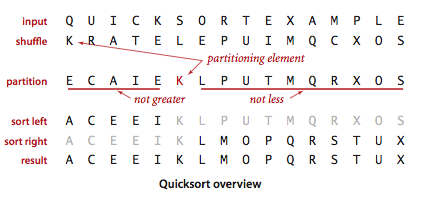
混洗是为了保证算法性能，下面分析性能时再说。随机打乱了数组，这里划分时直接选第一个元素为基准，再来 i，j 两个指针分别从首尾遍历，交换不符合的元素，最后再把基准值放到指针相遇的位置。

划分示意：

代码：

private static int partition(Comparable[] a, int lo, int hi) {
    int i = lo, j = hi+1;
    while (true) {
        // find item on left to swap
        while (less(a[++i], a[lo]))
            if (i == hi) break;

        // find item on right to swap
        while (less(a[lo], a[--j]))
            if (j == lo) break;

        if (i >= j) break;    // check if pointers cross
        exch(a, i, j);        // swap
    }

    exch(a, lo, j);    // swap with partitioning item
    return j;          // return index of item now known to be in place
}

划分例子：

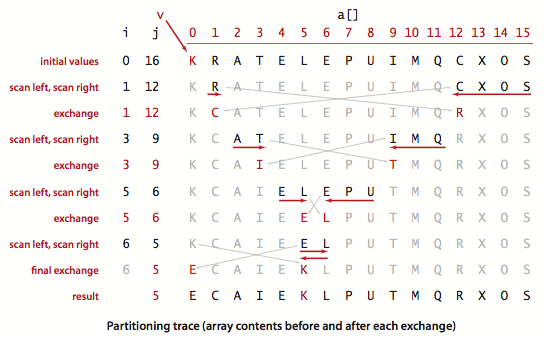
再递归地划分左右，得到基础的快排代码：

public class Quick {
    private static int partition(Comparable[] a, int lo, int hi) {
        /* as before */
    }

    public static void sort(Comparable[] a) {
        StdRandom.shuffle(a);
        sort(a, 0, a.length - 1);
    }

    private static void sort(Comparable[] a, int lo, int hi) {
        if (hi <= lo) return;
        int j = partition(a, lo, hi);
        sort(a, lo, j-1);
        sort(a, j+1, hi);
    }
}

排序过程轨迹示例：

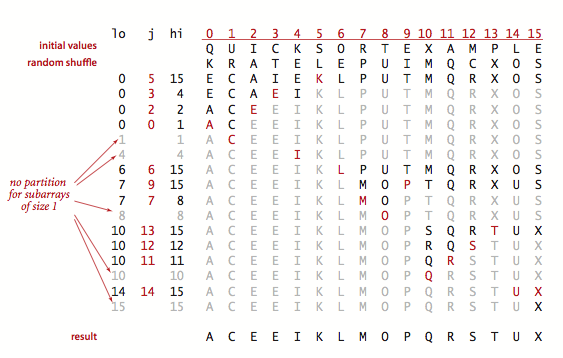
第一次划分选了 K，然后排左边，左边排好了再排 K 右边，小的数组也是这么个过程。

性能分析

最好情况下，每次划分选的元素都刚好把数组分成两半，这就有点像归并排序了，需要的比较次数是 NlgN 级别。最坏情况下，每次划分选的元素都是最小的，递归树就会很高，那需要的比较次数就是 \(N^{2}\) 级的。平均情况下，也就是排序之前随机打乱无重复（重复的下面会说）元素的数组，快排需要 ~2NlnN 次比较，证明：

\(C_{N}\) = \((N + 1)\) + \((\frac{C_{0} + C_{N-1}}{N})\) + \((\frac{C_{1} + C_{N-2}}{N})\) + ... + \((\frac{C_{N-1} + C_{0}}{N})\)

N + 1 是每次划分时需要的比较次数，基准值和其它 N - 1 个比较，i 和 j 相遇多比了两次，我觉得大概是这样理解。后面是递归排序的比较次数，因为划分基准选取每个位置的可能性是一样的，所以都带 \(\frac{1}{N}\)。等式两边乘 N，整理各项有：

\(NC_{N}\) = \(N(N + 1)\) + \(2(C_{0}\) + \(C_{1}\) + ... + \(C_{N-1}\))

上式减去 N-1 时的相同等式可得：

\(NC_{N}\) - \((N - 1)C_{N-1}\) = \(2N\) + \(2C_{N-1}\)

整理后再两边同时除以 N(N + 1) 得：

\(\frac{C_{N}}{N + 1}\) = \(\frac{C_{N-1}}{N}\) + \(\frac{2}{N + 1}\)

然后再看这张 PPT：

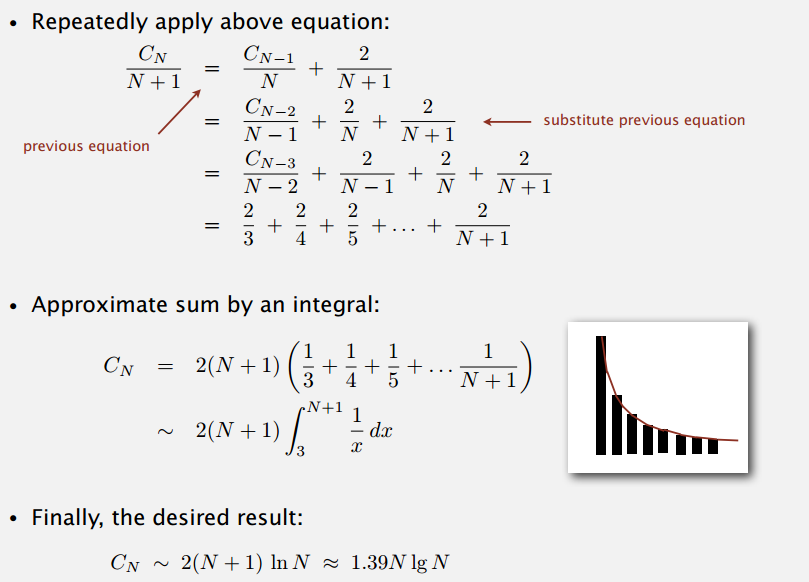
所以，平均情况下，快排需要的比较次数比归并排序多 39%，但实际上快排一般会比归并排序快，因为快排移动数据的次数更少。排序之前随机混洗，就是为了尽可能避免最坏情况，达到平均情况的表现，保证性能。

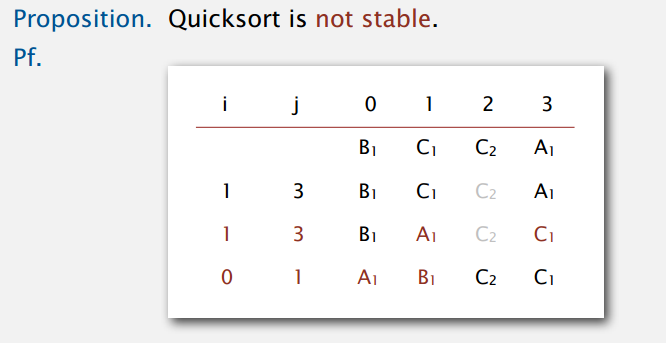
另外，快排是就地（in-place）排序，不需要额外空间。还有，快排不是稳定排序，交换可能改变相等元素的相对位置，图例：

算法改进

小数组用插入排序

和归并排序一样，快排也是递归的，处理小问题时的方法调用过于频繁，而且插入排序在小数组上很可能会更快。

private static void sort(Comparable[] a, int lo, int hi) {
    if (hi <= lo + CUTOFF - 1) {
        Insertion.sort(a, lo, hi);
        return;
    }
    int j = partition(a, lo, hi);
    sort(a, lo, j-1);
    sort(a, j+1, hi);
}

三抽样取中

人们发现将取样大小设为 3 并用大小居中的元素划分的效果最好。

private static void sort(Comparable[] a, int lo, int hi) {
    if (hi <= lo) return;

    int m = medianOf3(a, lo, lo + (hi - lo)/2, hi);
    swap(a, lo, m);

    int j = partition(a, lo, hi);
    sort(a, lo, j-1);
    sort(a, j+1, hi);
}

selection

现在我们来看一个和排序相关的问题，目标是找到一组数中第 K 大的数，这是另一个用理论指导的例子。显然可以对这组数直接排序，然后输出位置 K 的数，所以该问题的复杂度上界可以是 NlgN。当 K 很小的时候，比如 2，你可以遍历两次数组找到，这时上界还可以是 N 级别。另外，复杂度的下界也是 N，因为每个元素至少要访问一次，万一目标就是你漏掉的那个呢。于是乎，我们想要的该是一个线性级别的算法。

实际上，Hoare 在 1961 年的原论文（上面的基础版快排）里就介绍了基于划分（partition）的算法，平均情况下（先混洗）有线性级别的性能。

示意：

代码：

public static Comparable select(Comparable[] a, int k) {
    StdRandom.shuffle(a);
    int lo = 0, hi = a.length - 1;
    while (hi > lo) {
        int j = partition(a, lo, hi);
        if (j < k) lo = j + 1;
        else if (j > k) hi = j - 1;
        else return a[k];
    }
    return a[k];
}

最坏情况下还是 \(N^{2}\) 级别，但是有混洗，概率很低。实际上，有最坏情况下也能保证线性级别的算法，但太复杂而在实际中没有使用。啊对，那个证明，看看就好吧：

duplicate keys

实际应用中经常会出现含有大量重复元素的数组，而且经常排序的目的就是把某些值相等的元素归到一起，比如说按生日排员工资料等。归并排序，对于这种情况也一样处理，没差别，需要的比较次数还是在 1/2NlgN ~ NlgN，但很多课本上的快排会达到平方级别的时间，如果指针碰到和划分元素相等的元素时不停下来。

设想一个数组的元素都一样，在相等时不停止扫描，那尾指针就会一路扫到第二个位置，划分效果很差，递归排序子数组也是一样，直接达到 \(N^{2}\) 级别的复杂度。相等时停止扫描的话，会刚好把数组对半分，递归下去，复杂度是 NlgN 的。但其实，对半分里面的元素交换根本就是没有必要的，我们想尽量地把相等元素放在原地。于是乎，很自然的一个想法是改进划分，最后分成小于，等于和大于三个部分。

Accomplishing this partitioning was a classical programming exercise popularized by E. W. Dijkstra as the Dutch National Flag problem, because it is like sorting an array with three possible key values, which might correspond to the three colors on the flag.

-- booksite.23quicksort

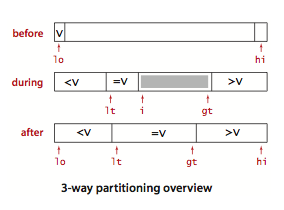
Dijkstra 的方法：

• 将划分元素 a[lo] 记做 v。

• 从左到右扫描数组，下标为 i。

  • (a[i] < v)：交换 a[lt] 和 a[i]；lt 和 i 都加一
  • (a[i] > v)：交换 a[gt] 和 a[i]；gt 减一
  • (a[i] == v)：i 加一

示意图：

代码：

private static void sort(Comparable[] a, int lo, int hi) {
    if (hi <= lo) return;
    int lt = lo, gt = hi;
    Comparable v = a[lo];
    int i = lo;
    while (i <= gt) {
        int cmp = a[i].compareTo(v);
        if (cmp < 0) exch(a, lt++, i++);
        else if (cmp > 0) exch(a, i, gt--);
        else i++;
    }

    sort(a, lo, lt - 1);
    sort(a, gt + 1, hi);
}

划分轨迹示例：

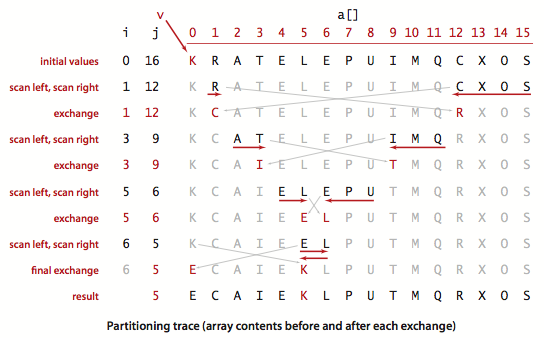
说是熵最优的排序，对大多数情况可以把线性对数级（linearithmic）的性能提高到线性级别，看看就好，看看就好。。

system sorts

最后一节介绍了些系统排序有的没的，贴些课件体会下。

Java 对象排序用归并，课程说可能是设计者觉得用户都用对象了，那归并的额外空间该是也可以接受的，原始数据类型大概就比较看重性能，就用快排。这个好像也有其他说法，反正随便啦。

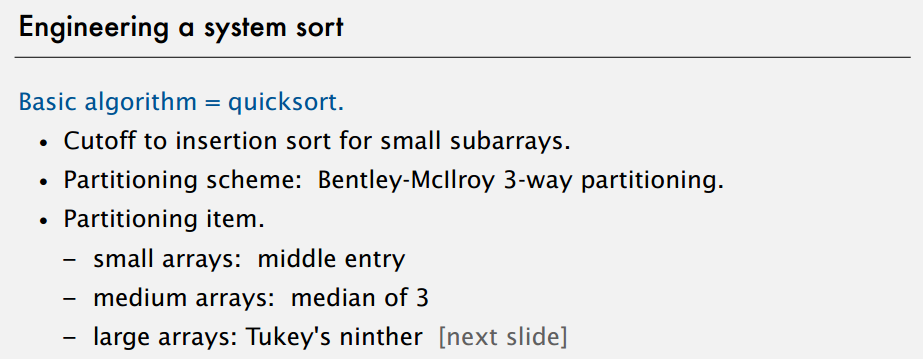
上面对排序一顿改进，好像很厉害的样子，不过课程说有杀手输入会让它崩溃，booksite 上有提到这部分：

Antiquicksort. The algorithm for sorting primitive types in Java is a variant of 3-way quicksort developed by Bentley and McIlroy. It is extremely efficient for most inputs that arise in practice, including inputs that are already sorted. However, using a clever technique described by M. D. McIlroy in A Killer Adversary for Quicksort, it is possible to construct pathological inputs that make the system sort run in quadratic time. Even worse, it overflows the function call stack. To see the sorting library in Java 6 break, here are some killer inputs of varying sizes: 10,000, 20,000, 50,000, 100,000, 250,000, 500,000, and 1,000,000. You can test them out using the program IntegerSort.java which takes a command line input N, reads in N integers from standard input, and sorts them using the system sort.

所以，总之课程还是偏向排序前混洗下数组吧。然后，说到该怎么选择排序算法，可以考虑稳定性，时间复杂度，空间复杂度等，一般系统排序也够用了，最后贴上目前接触到的小总结。