Mergesort

归并排序

归并排序和快速排序是两个经典的排序算法，是计算机的基础设施的重要组成部分，完整科学地理解它们的特性有助于我们将其用于实际的系统排序，快排也是二十世纪科学和工程领域的十大算法之一。

mergesort

归并排序基本思想：把数组分成两半，递归地排好每一半，合并有序的两半。另外，冯诺依曼被公认为“归并排序之父”。

合并操作并不复杂，需要先拷贝到一个辅助数组，然后子数组从头开始对应比较，看先放哪个。

代码：

private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
    assert isSorted(a, lo, mid);        // precondition: a[lo..mid] sorted
    assert isSorted(a, mid + 1, hi);    // precondition: a[mid + 1..hi] sorted

    for (int k = lo; k <= hi; k++)
        aux[k] = a[k];

    int i = lo, j = mid + 1;
    for (int k = lo; k <= hi; k++) {
        if (i > mid) a[k] = aux[j++];
        else if (j > hi) a[k] = aux[i++];
        else if (less(aux[j], aux[i])) a[k] = aux[j++];
        else a[k] = aux[i++];
    }

    assert isSorted(a, lo, hi);    // postcondition: a[lo..hi] sorted
}

上面用到了 Java 中的 assert，会在后面的布尔值为假时抛出异常，isSorted() 在 Elementary Sorts 第一部分的最后有。这有助于发现程序的错误，而且你可以禁用它，不会在产品中产生额外的代码。

再加上递归，归并排序的完整代码如下：

public class Merge {
    private static void merge(...) {
        /* as before */
    }

    private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
        if (hi <= lo) return;
        int mid = lo + (hi - lo) / 2;
        sort(a, aux, lo, mid);
        sort(a, aux, mid + 1, hi);
        merge(a, aux, lo, mid, hi);
    }

    public static void sort(Comparable[] a) {
        Comparable[] aux = new Comparable[a.length];
        sort(a, aux, 0, a.length - 1);
    }
}

注意不要递归地创建辅助数组，这会让代码的效率变差，上面只在递归外创建一次辅助数组。

归并排序的轨迹示例：

排好最前两，再排后面两，并起来排好前四，类似排好后面四个，并起来排好前八，一样排好后八，并起来排好整个数组。这样的轨迹图，有助于我们理解递归发生了什么。

对于长度为 N 的任意数组，归并排序至多需要 NlgN 次的比较和 6NlgN 次的数组访问。

合并的时候最多需要比较 N 次（后来私以为最多只要 N-1 次，你想每次比较至少确定一个，最后一个不用比，那最多不就 N-1 吗），访问数组包括复制到辅助数组的 2N，比较完放回去的 2N，以及最多 N 次比较时的 2N 次访问。

当 N 为 2 的幂时，比较次数最多为 NlgN 比较好证明，课程甚至列了三：

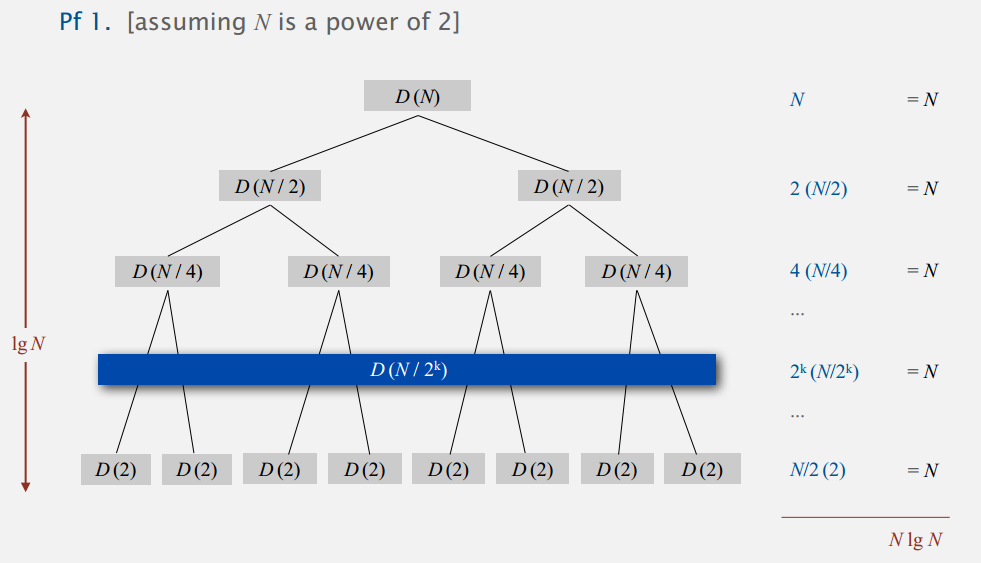
对于一般的 N，最后的准确值会更复杂些，反正还是 NlgN 级别的。总之，归并排序的时间复杂度是 NlgN 级别，但是因为有辅助数组，需要的空间和 N 成正比。也有不用辅助数组改成就地排序的，但太复杂不实用。另外，我们还可以对上面的代码做点改进。

对小规模数组用插入排序

递归会使小规模问题中方法的调用过于频繁，而且插入排序很可能在小数组上比归并更快。

private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
    if (hi <= lo + CUTOFF - 1) {
        Insertion.sort(a, lo, hi);
        return;
    }
    int mid = lo + (hi - lo) / 2;
    sort(a, aux, lo, mid);
    sort(a, aux, mid + 1, hi);
    merge(a, aux, lo, mid, hi);
}

CUTOFF 可设为 7 或 15 这些比较小的数。

测试数组是否有序

如果左边最大小于右边最小，就可以跳过合并，对于子数组有序的数组有帮助，而且只要一行。

private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
    ...
    if (!less(a[mid + 1], a[mid])) return;
    merge(a, aux, lo, mid, hi);
}

不要复制到辅助数组

每次合并直接合到辅助数组上，下次再交换角色让原数组当辅助，省去了原来复制数据的时间。

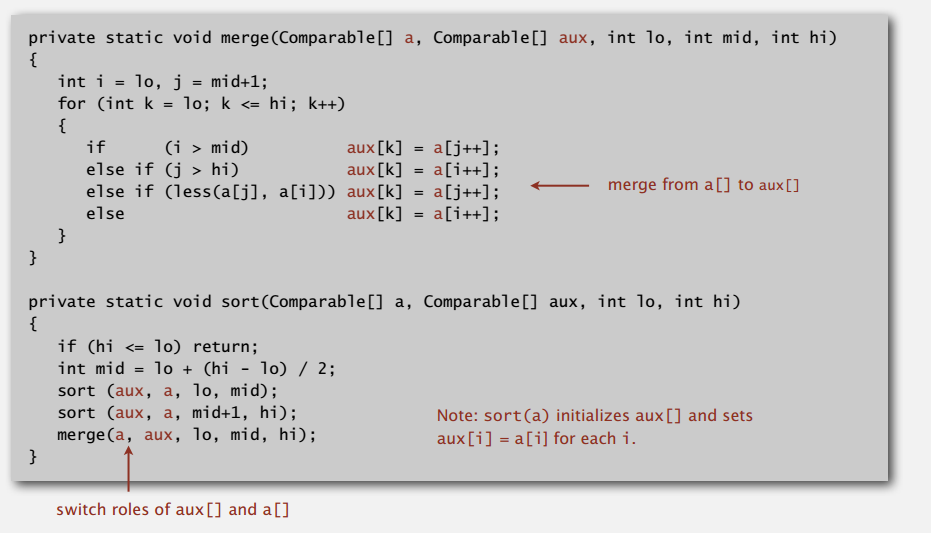
MergeX.java 实现了上述改进版归并排序，里面的 sort():

public static void sort(Comparable[] a) {
        Comparable[] aux = a.clone();
        sort(aux, a, 0, a.length-1);  
        assert isSorted(a);
    }

输入的待排序数组在第二个参数。

bottom-up mergesort

自底向上的递归排序和前面的分治反过来，不需要递归，逻辑上更简单，排序过程示意：

遍历数组，合并长度为 1 的子数组，再遍历合并长度为 2 的数组，重复合并长度为 4，8，16，... 的子数组，最后合并成排好序的原数组。

代码：

public class MergeBU {
    private static void merge (...) {
        /* as before */
    }

    private static void sort(Comparable[] a) {
        int N = a.length;
        Comparable[] aux = new Comparable[N];
        for (int sz = 1; sz < N; sz = sz+sz)
            for (int lo = 0; lo < N-sz; lo += sz+sz)
                merge(a, aux, lo, lo+sz-1, Math.min(lo+sz+sz-1, N-1));
    }
}

注意看代码上面轨迹图里的 size 和 lo，比较容易读懂代码，合并最后一个参数是为了处理大小不为 2 的幂的数组，比如：

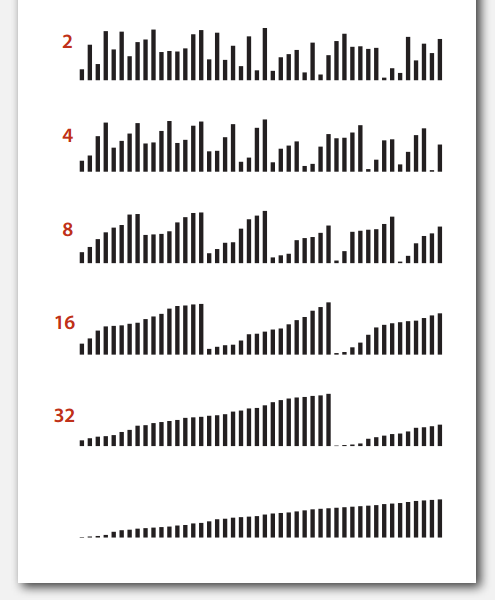
sorting complexity

研究复杂度的第一步是建立计算模型，这里我们讨论基于比较的排序算法，即只能通过比较获得信息，排序过程自然地可以抽象成决策树（decision tree）:

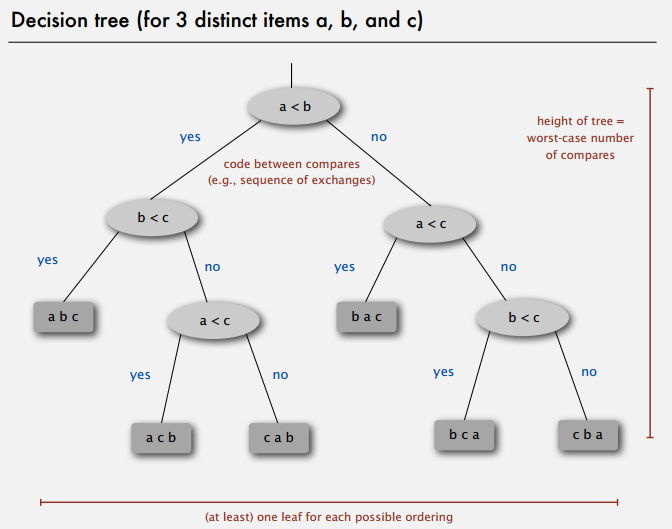
复杂度即树高（比较次数），可以证明：任何基于排序的算法至少需要 lg(N!) ~ NlgN 次比较。

对于大小为 N 的待排序列，一共有 N! 种可能的排列组合，决策树至少要有 N! 片叶子与其对应，不然算法无法处理遗漏的那些情况。另外，对于高度为 h 的决策树，这里也是二叉树，最多有 \(2^{h}\) 片叶子，所以有 \(N! \leq leaves \leq 2 ^{h}\)。于是，树高 h （比较次数）至少为 lg(N!)，根据 Stirling 公式近似为 NlgN。

复杂度分析有助于算法设计，寻找最优算法，像结合上面来看，归并排序就是一种渐进最优的基于比较的算法。但是归并排序的空间复杂度不是最优的，除了比较的其他操作（如访问数组）也可能很重要，所以这并不是结束。

comparators

Java 可比较（Comparable）接口一般实现的是自然的比较顺序，像 Data 类就按日期大小，比较器（Comparator）可以让我们方便地用其它的顺序，比如：

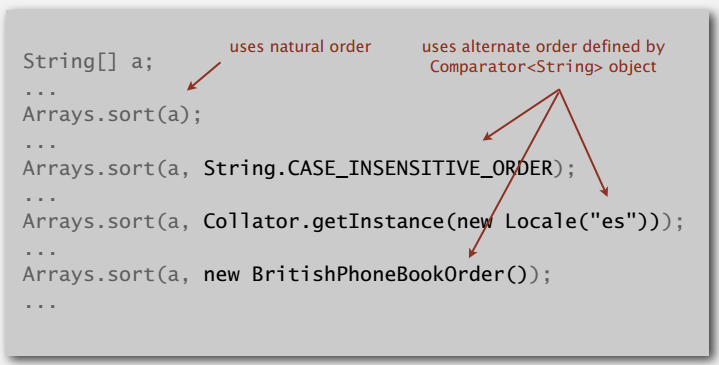
支持传入比较器的插入排序：

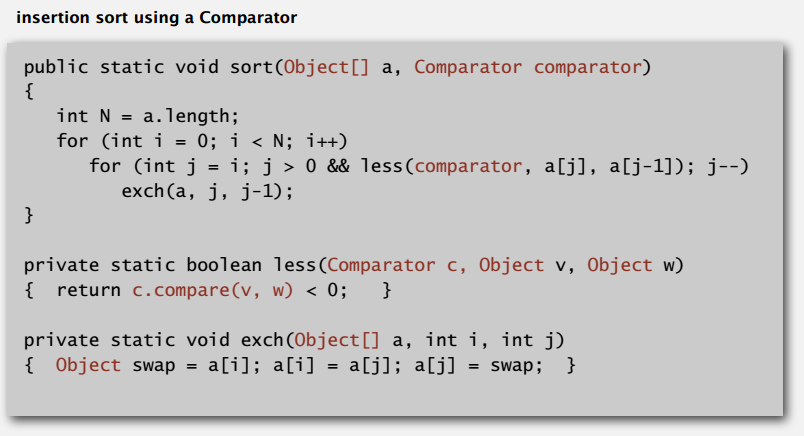
比较器下要实现 compare() 方法，返回值和 Comparable 下的 compareTo() 方法类似，同样要是全序关系。

// public Interface Comparator<Key> {
    int compare(Key v, Key w)    // compare keys v and w
}

于是乎，现在我们来实现 Elementary Sorts 最后的极角比较。按数学方法算三角函数啥的开销太大，继续使用判断是否为逆时针顺序那个来做。

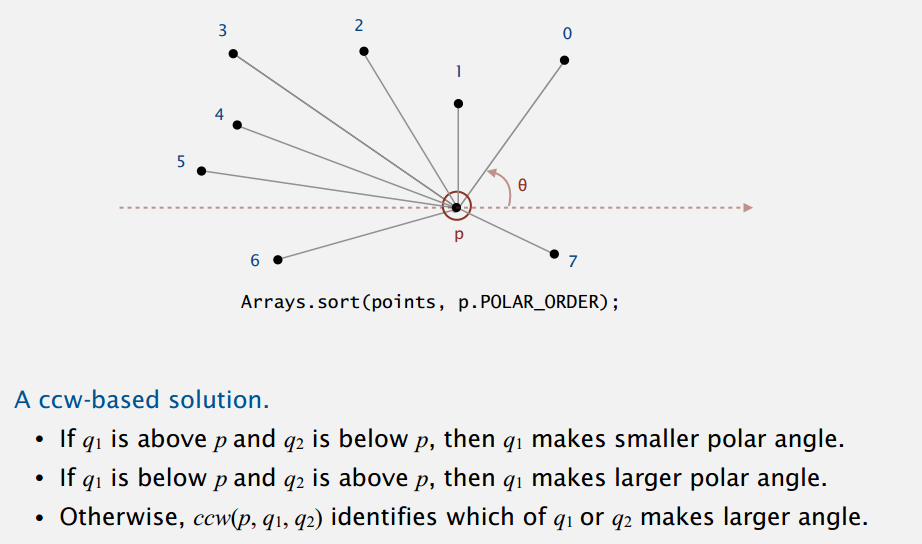
代码：

public class Point2D {
    public final Comparator<Point2D> POLAR_ORDER = new PolarOrder();
    private final double x, y;

    public Point2D(double x, double y) {
        this.x = x;
        this.y = y;
    }

    /**
     * Returns true if a→b→c is a counterclockwise turn.
     * @param a first point
     * @param b second point
     * @param c third point
     * @return { -1, 0, +1 } if a→b→c is a { clockwise, collinear; counterclocwise } turn.
     */
    private static int ccw(Point2D a, Point2D b, Point2D c) {
        double area2  = (b.x-a.x)*(c.y-a.ay) - (b.y-a.y)*(c.x-a.x);
        if (area2 < 0) return -1;         // clockwise
        else if (area2 > 0) return +1;    // counter-clockwise
        else return 0;                    // collinear
    }

    // compare other points relative to polar angle (between 0 and 2pi) they make with this Point
    private class PolarOrder implements Comparator<Point2D> {
        public int compare(Point2D q1, Point2D q2) {
            double dx1 = q1.x - x;
            double dy1 = q1.y - y;
            double dx2 = q2.x - x;
            double dy2 = q2.y - y;

            if (dy1 >= 0 && dy2 < 0) return -1;         // q1 above; q2 below
            else if (dy2 >= 0 && dy1 < 0) return +1;    // q1 below; q2 above
            else if (dy1 == 0 && dy2 == 0) {            // 3-collinear and horizontal
                if (dx1 >= 0 && dx2 < 0) return -1;
                else if (dx2 >= 0 && dx1 < 0) return +1;
                else return 0;
            }
            else return -ccw(Point2D.this, q1, q2);    // both above or below
        }
    }
}

完整的参见：Point2D.java，还有 GrahamScan.java。

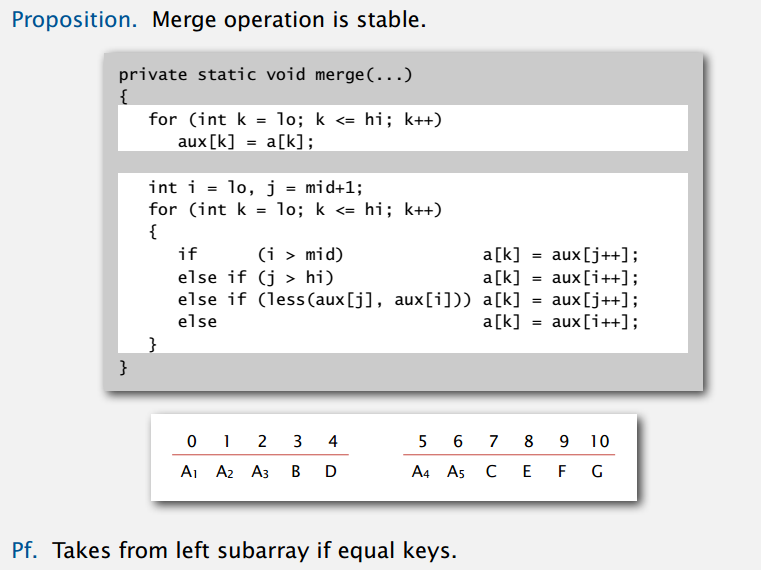
stability

如果数组里相等元素的相对位置在排序之后没有改变，那么就称这个算法具有稳定性（stability）。意义在于，比如你按学号排完学生，然后再按成绩排，稳定算法可以让成绩一样的学生的学号还是有序的。

上篇实现的插入排序具有稳定性，只会插到较大的元素前面，而不会越过相等的元素。选择排序不是稳定的，长距离的交换有可能破坏稳定性，如：

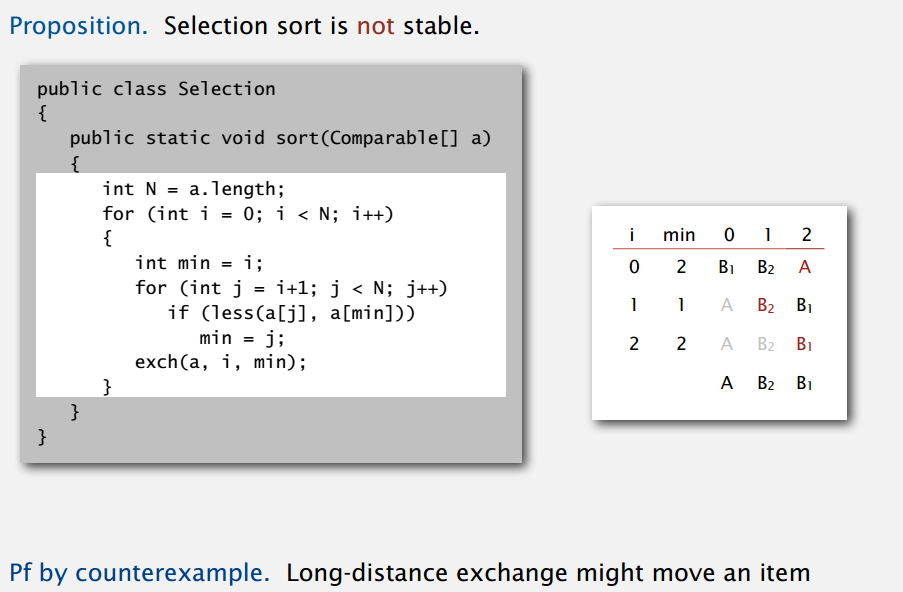
同理，希尔排序也是不稳定的。至于归并排序，在合并碰到相等元素时取左子数组的，就是稳定的。