HDU 4445 纯物理题+枚举

Crazy Tank

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 6047    Accepted Submission(s): 1318

Problem Description

Crazy Tank was a famous game about ten years ago. Every child liked it. Time flies, children grow up, but the memory of happy childhood will never go.

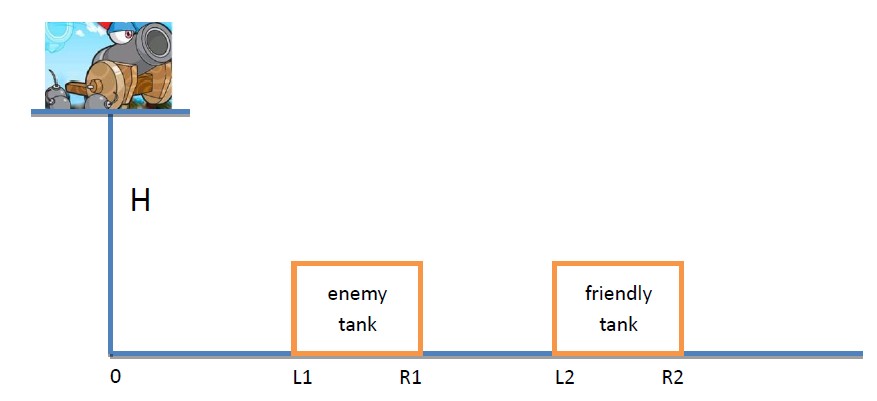
Now you’re controlling the tank Laotu on a platform which is H meters above the ground. Laotu is so old that you can only choose a shoot angle(all the angle is available) before game start and then any adjusting isnot allowed. You need to launch N cannonballs and you know that the i-th cannonball’s initial speed is Vi.
On the right side of Laotu There is an enemy tank on the ground with coordination(L1, R1) and a friendly tank with coordination(L2, R2). A cannonball is considered hitting enemy tank if it lands on the ground between [L1,R1] (two ends are included). As the same reason, it will be considered hitting friendly tank if it lands between [L2, R2]. Laotu's horizontal coordination is 0.
The goal of the game is to maximize the number of cannonballs which hit the enemy tank under the condition that no cannonball hits friendly tank.
The g equals to 9.8.

 

Input

There are multiple test case.
Each test case contains 3 lines.
The first line contains an integer N(0≤N≤200), indicating the number of cannonballs to be launched.
The second line contains 5 float number H(1≤H≤100000), L1, R1(0<L1<R1<100000) and L2, R2(0<L2<R2<100000). Indicating the height of the platform, the enemy tank coordinate and the friendly tank coordinate. Two tanksmay overlap.
The third line contains N float number. The i-th number indicates the initial speed of i-th cannonball.
The input ends with N=0.

 

Output

For each test case, you should output an integer in a single line which indicates the max number of cannonballs hit the enemy tank under the condition that no cannonball hits friendly tank.

 

Sample Input

2
10 10 15 30 35
10.0
20.0
2
10 35 40 2 30
10.0
20.0
0

 

Sample Output

1
0
Hint
In the first case one of the best choices is that shoot the cannonballs parallelly to the horizontal line, then the first 
cannonball lands on 14.3 and the second lands on 28.6.
In the second there is no shoot angle to make any cannonball land between [35,40] on the condition that no 
cannonball lands between [2,30].
 

 

Source

2012 Asia JinHua Regional Contest

题意：一个大炮在高度为H的地方连续发射炮弹，要求炮弹落在敌方坦克上，不能落在友方上，先固定发射的角度，然后角度不能变了，打出所有的炮弹。

思路：纯物理题啊，当时考虑到向上发射和向下发射两种情况，把问题标量化了，结果求向下发射的时间还要用求根公式，这样就麻烦了。其实想想回忆以前高中所学，我们可以把这个问题矢量化，取向下为正方向，速度用位移(位移的变化也就是H，省去中间路程的考虑),时间用竖直分量下的速度矢量变化来求得，这样就简化了求水平位移的求解。
角度转弧度，也就是 度数*π/180，一个π也就是180°，我们一般用sin1/6π = 1/2。向下向上发射的角度也就是180°，一个π的范围，可以分为1000份，每次枚举增加π/1000大笑，满足则++。

主要就是Vy*Vy-Vy0*Vy0=2gH，这个公式的理解，毕竟高中过去那么久了，对矢量位移的变化公式理解差点就忘了。

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstdio>
using namespace std;
const int MAXN=200+5;
const double PI=acos(-1.0);//定义π大小
const double g=9.8;
double v[MAXN],L1,R1,L2,R2,H;
int n;

int meiju(double x)//角度为x;
{
    int ans=0;
    for(int i=0;i<n;i++)
    {
        double Vy0=v[i]*sin(x); //竖直分量的初速度，当向上发射时，为-PI，初速度的竖直分量为负
        double Vx0=v[i]*cos(x); //水平分量的速度不变
        double Vy=sqrt(2*g*H+Vy0*Vy0); //矢量位移公式Vy*Vy-Vy0*Vy0=2gH，H为竖直分量上的位移大小。注意规定向下为正方向后，Vy肯定为正数，绝对值直接去掉
        double t=(Vy-Vy0)/g; //如果Vy0是向上打的，则为负，速度变化量相当于两个速度的相加，除以加速度，得出时间
        double d=Vx0*t;
        
        if(d>=L2&&d<=R2)
            return 0;
        if(d>=L1&&d<=R1)
            ans++;
    }
    return ans;
}
int main()
{
    while(scanf("%d",&n)!=EOF && n)
    {
        scanf("%lf%lf%lf%lf%lf",&H,&L1,&R1,&L2,&R2);
        for(int i=0;i<n;i++)
          scanf("%lf",&v[i]);
          
        double add=PI/1000;//最好分细一点
        
        int ans=0;

        for(double x=-PI/2;x<=PI/2;x+=add) //角度从竖直向上开始打到竖直向下，一个π的范围
          ans=max(ans,meiju(x));
        printf("%d\n",ans);
    }
    return 0;
}