【数据结构】平衡树splay和fhq—treap
1.BST二叉搜索树
顾名思义,它是一棵二叉树。
它满足一个性质:每一个节点的权值大于它的左儿子,小于它的右儿子。
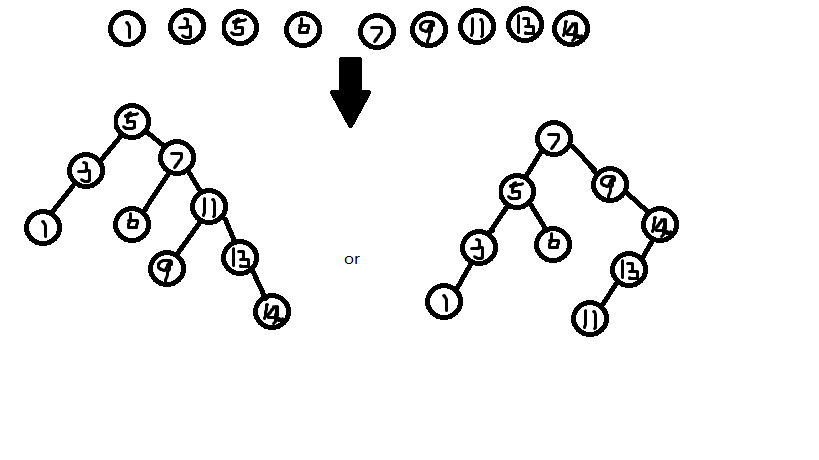
当然不只上面那两种树的结构。
那么根据性质,可以得到该节点左子树里的所有值都比它小,右子树的都比它大。
而平衡树都是基于BST的。
为什么叫做平衡树?对于数的操作可能会破坏BST的性质,这时会进行另外的操作,保持它的性质。
为什么要用BST?对于一棵BST,每一次的操作,都相当于进行一次二分,时间复杂度可以降到log级别。
这里写的是两个常用的平衡树。
2.Splay
splay树是基于一个rotate(旋转)函数和splay(伸展)函数来保证平衡。
初始化
struct Splay_Tree{int son[2],fa,size,cnt,val;}T[N]; #define ls(x) T[x].son[0]//左儿子 #define rs(x) T[x].son[1]//右儿子 #define fa(x) T[x].fa//当前点他爹 #define sze(x) T[x].size//以当前点为根的树的大小 #define cnt(x) T[x].cnt//当前点的出现次数 #define val(x) T[x].val//当前点的权值 //不为别的,小括号看起来爽一点
rotate
例如,我们要将下图的x点右旋:

可以手推一下,总结:
rotate要影响3个点:x,y(x的父亲),z(y的父亲,x的爷爷);
y是z的k儿子(k用来判断左儿子,还是右儿子,0是左儿子,1是右儿子,用^1进行切换),则x就变成z的k儿子;
x的k^1儿子变成y的k儿子,y变成x的k^1儿子。
(想不到怎么描述了,只能这么瞎逼逼)
inline void rotate(int x){ int y=fa(x),z=fa(y); int k=(rs(y)==x),w=T[x].son[k^1]; T[z].son[rs(z)==y]=x,fa(x)=z; T[y].son[k]=w,fa(w)=y; T[x].son[k^1]=y,fa(y)=x; update(y),update(x); }
update就是个实时更新
splay
这一步是要将x点旋转到goal的儿子的位置
那么怎么做呢?循环就行了。但是还有一种特殊情况,由于这种情况都满足被旋转点和父节点都是左节点或者是右儿子,我们姑且称它为三点一线,先看图:
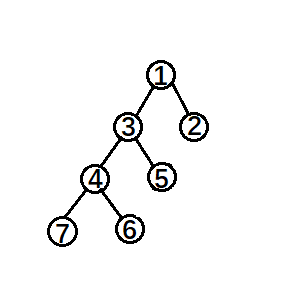
比如说我们这里要splay④,如果直接把④一直旋转到根节点的话就会是这样:

可以看见③还是①的左节点,相当于只是改变了④和①的关系,专业一点就是说形成了单旋使平衡树失衡。而解决的方法就是在出现三点一线时先旋转它的父节点避免单旋,正确的应该是这样:

inline void splay(int x,int goal){ while(fa(x)!=goal){ int y=fa(x),z=fa(y); if(z!=goal) (y==ls(z))^(x==ls(y))?rotate(x):rotate(y); rotate(x); } if(!goal) root=x; }
insert
我们要先从根节点一直向下找到该插入的位置,若该节点已存在,cnt++就行,否则造一个新的点,别忘了splay保证平衡:
inline void insert(int x){ int u=root,father=0; while(u&&val(u)!=x){ father=u; u=T[u].son[x>val(u)]; } if(u) cnt(u)++; else{ u=++tot; if(father) T[father].son[x>val(u)]=u; ls(u)=rs(u)=0;fa(u)=father,val(u)=x,cnt(u)=sze(u)=1; } splay(u,0); }
find
这是找到权值为val的点的位置,代码很好理解:
inline void find(int x){ int u=root; if(!u) return ; while(t[u].son[x>t[u].val]&&x!=t[u].val) u=t[u].son[x>t[u].val]; splay(u,0); }
search
找前后驱。这里都打在了一个函数里,用0表示找前驱,1找后驱。
inline int search(int x,int tmp){//找前后驱 find(x); int u=root; if(t[u].val<x&&!tmp) return u; if(t[u].val>x&&tmp) return u; u=t[u].son[tmp]; while(t[u].son[tmp^1]) u=t[u].son[tmp^1]; //这里蛇皮走位,而不是一直大或者一直小 return u; }
delete
删除操作。先找到前后驱,将前驱旋转至根,而将后驱旋转至前驱的右儿子。
这时要删除的点就单独的呆在了后驱的左儿子的位置。
如果cnt>1,cnt--;否则将该点变为0
inline void delet(int x){ int pre=search(x,0),suf=search(x,1); splay(pre,0),splay(suf,pre); int del=t[suf].son[0]; if(t[del].cnt>1){t[del].cnt--;splay(del,0);} else t[suf].son[0]=0; }
排名询问
find一遍,x的左儿子的大小+1就是排名
第k大的数
自根向下找,很好理解:
inline int search_value(int x){ int u=root; if(t[u].size<x) return 0; while(1){ int v=t[u].son[0]; if(x>t[v].size+t[u].cnt){ x-=t[v].size+t[u].cnt; u=t[u].son[1]; } else if(t[v].size>=x) u=v; else return t[u].val; } }
就是把上面的函数给混在一起:

#include<cstdio> using namespace std; const int maxn=201000; int root,tot; struct tree{int son[2],fa,cnt,val,size;}t[maxn]; inline void update(int x){t[x].size=t[t[x].son[0]].size+t[t[x].son[1]].size+t[x].cnt;} inline void rotate(int x){ int y=t[x].fa,z=t[y].fa; int k=(t[y].son[1]==x); t[z].son[(t[z].son[1]==y)]=x; t[x].fa=z; t[y].son[k]=t[x].son[k^1]; t[t[x].son[k^1]].fa=y; t[x].son[k^1]=y; t[y].fa=x; update(y),update(x); } inline void splay(int x,int goal){ while(t[x].fa!=goal){ int y=t[x].fa,z=t[y].fa; if(z!=goal) (t[z].son[0]==y)^(t[y].son[0]==x)?rotate(x):rotate(y); rotate(x); } if(!goal) root=x; } inline void find(int x){ int u=root; if(!u) return ; while(t[u].son[x>t[u].val]&&x!=t[u].val) u=t[u].son[x>t[u].val]; splay(u,0); } inline void insert(int x){ int u=root,father=0; while(u&&t[u].val!=x){ father=u; u=t[u].son[x>t[u].val]; } if(u) t[u].cnt++; else{ u=++tot; if(father) t[father].son[x>t[father].val]=u; t[u].son[0]=t[u].son[1]=0; t[tot].fa=father,t[tot].val=x,t[tot].cnt=t[tot].size=1; } splay(u,0); } inline int search(int x,int tmp){//找前后驱 find(x); int u=root; if(t[u].val<x&&!tmp) return u; if(t[u].val>x&&tmp) return u; u=t[u].son[tmp]; while(t[u].son[tmp^1]) u=t[u].son[tmp^1]; return u; } inline void delet(int x){ int pre=search(x,0),suf=search(x,1); splay(pre,0),splay(suf,pre); int del=t[suf].son[0]; if(t[del].cnt>1){t[del].cnt--;splay(del,0);} else t[suf].son[0]=0; } inline int search_value(int x){ int u=root; if(t[u].size<x) return 0; while(1){ int v=t[u].son[0]; if(x>t[v].size+t[u].cnt){ x-=t[v].size+t[u].cnt; u=t[u].son[1]; } else if(t[v].size>=x) u=v; else return t[u].val; } } signed main(){ int n;scanf("%d",&n); insert(1e9),insert(-1e9); while(n--){ int opt,x; scanf("%d%d",&opt,&x); if(opt==1) insert(x); if(opt==2) delet(x); if(opt==3){ find(x);printf("%d\n",t[t[root].son[0]].size);} if(opt==4) printf("%d\n",search_value(x+1)); if(opt==5) printf("%d\n",t[search(x,0)].val); if(opt==6) printf("%d\n",t[search(x,1)].val); } return 0; }
区间操作
其实思想类似于线段树,找到那个区间,对那个区间进行操作

#include<cstdio> #include<algorithm> using namespace std; inline int read(){ int sum=0;bool flag=true;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')flag=false;ch=getchar();} while(ch>='0'&&ch<='9'){sum=sum*10+ch-'0';ch=getchar();} return (flag?sum:-sum); } inline void print(int x){ if(x<0) putchar('-'),x=-x; while(x>=10) print(x/10); putchar(x%10+'0'); } const int maxn=101000; int root,tot,tag[maxn],key[maxn],ans[maxn]; struct tree{int son[2],fa,cnt,val,size;}t[maxn]; inline void update(int x){t[x].size=t[t[x].son[0]].size+t[t[x].son[1]].size+1;} inline void pushdown(int x){ if(tag[x]){ tag[t[x].son[0]]^=1,tag[t[x].son[1]]^=1; swap(t[x].son[0],t[x].son[1]); tag[x]=0; } } inline int getson(int x){return t[t[x].fa].son[1]==x;} inline void rotate(int x){ int y=t[x].fa,z=t[y].fa,tt=getson(x); if(z) t[z].son[getson(y)]=x; else root=x; t[x].fa=z; int tmp=t[x].son[!tt]; if(tmp) t[tmp].fa=y; t[y].son[tt]=tmp; t[x].son[!tt]=y; t[y].fa=x; update(y),update(x); } inline void splay(int x,int goal){ while(t[x].fa!=goal){ int y=t[x].fa,z=t[y].fa; if(z!=goal) (getson(y)==getson(x))?rotate(y):rotate(x); rotate(x); } } inline int find(int x){ int u=root; while(1){ pushdown(u); if(t[u].son[0]&&x<=t[t[u].son[0]].size) u=t[u].son[0]; else{ int tmp=(t[u].son[0]?t[t[u].son[0]].size:0)+1; if(x==tmp) return u; x-=tmp; u=t[u].son[1]; } } } inline int build(int l,int r,int tmp){ int mid=(l+r)>>1; t[mid].fa=tmp; key[mid]=ans[mid]; if(l<mid) t[mid].son[0]=build(l,mid-1,mid); if(r>mid) t[mid].son[1]=build(mid+1,r,mid); update(mid); return mid; } inline void work(int x){ pushdown(x); if(t[x].son[0]) work(t[x].son[0]); ans[++tot]=key[x]; if(t[x].son[1]) work(t[x].son[1]); } signed main(){ int n=read(),m=read(); for(int i=1;i<=n+2;i++) ans[i]=i-1; root=build(1,n+2,0); while(m--){ int l=read(),r=read(); l=find(l),r=find(r+2); splay(l,0);splay(r,l); tag[t[t[root].son[1]].son[0]]^=1; } work(root); for(int i=1;i<=n;i++) printf("%d ",ans[i+1]); return 0; }
3*.Treap
Treap是Tree和Heap,所以很明显有heap(堆)的性质。
怎样保证BST的性质的同时保证堆的性质?
对每一个节点,有两个值,一个是权值,另一个是rnd随机值,来决定优先级。
而两个同时限制,那么旋转时会很麻烦。
对,所以我没学。淦~~~
但其实会了splay和fhq—treap,这个treap也没有学习的必要了
对了,机房大佬表示Treap是真的菜
4.fhq-Treap
名字叫treap,但和treap之间的相同处,也只是同为带有随机附加域满足堆的性质的二叉搜索树。
FHQ-Treap,又名非旋Treap,是范浩强大爷在某些奇特的灵感之下发明的一种平衡树
这里只需要了解2个主要操作,便可处理很多问题,包括可持久化。
split(分解)和merge(合并)
还需要运用2个另外的树,x和y,只是用来记录临时分裂的两棵树的根节点,因为树无旋,所以根节点下的树唯一确定。
split
递归进行分解,比该点权值小的放在x树上,比它大的放在y树上,同时实时更新。
当然权值分裂后还有排名(rnd值)分裂,这里只放了权值分裂。
inline void split(int id,int k,int &x,int &y){ if(!id){x=y=0;return ;} if(val[id]<=k){ x=id; split(rs(id),k,rs(id),y); } else{ y=id; split(ls(id),k,x,ls(id)); } update(id); }
merge

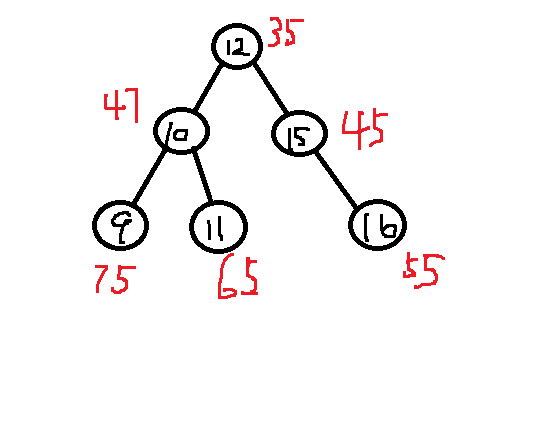
最后得到如下的树:
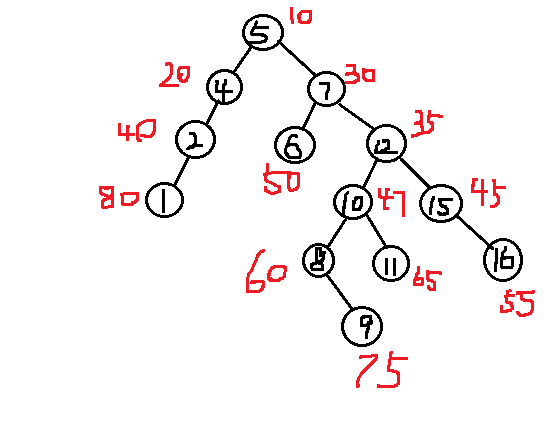
inline int merge(int a,int b){
if(!a || !b) return a+b; if(rnd[a] < rnd[b]){ rs(a)=merge(rs(a),b); update(a);return a; } else{ ls(b)=merge(a,ls(b)); update(b);return b; } }
find
这里我的find函数是找到以该点为根的树的排名为k的数的位置,同样是去看左子树的大小。
inline int find(int id,int k){//返回的以id为根的树的第k个数的位置 while(true){ if(k<=sze[ls(id)]) id=ls(id); else if(k==sze[ls(id)]+1) return id; else k-=sze[ls(id)]+1,id=rs(id); } }
insert
从根节点开始分裂,然后依次合并x树和该点,再合并y树。
inline int new_node(int x){ sze[++cnt]=1; val[cnt]=x; rnd[cnt]=rand(); return cnt; } inline void insert(int val){ split(root,val,x,y); root=merge(merge(x,new_node(val)),y); }
delete
在用一棵临时树z,先从根节点按val分裂,再从x节点按val-1分裂,最后按顺序有依次合并。
inline void delet(int val){ split(root,val,x,z); split(x,val-1,x,y); y=merge(ls(y),rs(y)); root=merge(merge(x,y),z); }
排名询问
按val-1去分裂,左子树的大小+1就是排名,别忘了merge回去。
inline void query_rank(int val){ split(root,val-1,x,y);
print(sze[x]+1); root=merge(x,y); }
第k大的数
用find函数就行
找前后驱
同理,还是先split,再merge。

#pragma GCC optimize(3) #include<cstdio> #include<iostream> #include<algorithm> #include<cctype> #include<cstdlib> #include<ctime> using namespace std; inline int read(){ int s=0;bool flag=true;char ch=getchar(); while(!isdigit(ch)){if(ch=='-')flag=false;ch=getchar();} while(isdigit(ch)){s=(s<<3)+(s<<1)+ch-'0';ch=getchar();} return flag?s:-s; } inline void write(int x){ if(x<0) x=-x,putchar('-'); if(x>9) write(x/10); putchar(x%10+'0'); } inline void print(int x){write(x);puts("");} const int N=5e5+10; int root,x,y,z,cnt; struct Treap{ int ch[N][2],val[N],rnd[N],sze[N]; #define ls(id) ch[id][0] #define rs(id) ch[id][1] inline void update(int x){sze[x]=sze[ch[x][0]]+sze[ch[x][1]]+1;} inline void split(int id,int k,int &x,int &y){ if(!id){x=y=0;return ;} if(val[id]<=k){x=id;split(rs(id),k,rs(id),y);} else{y=id;split(ls(id),k,x,ls(id));} update(id); } inline int merge(int a,int b){ if(!a || !b) return a+b; if(rnd[a] < rnd[b]){ rs(a)=merge(rs(a),b); update(a);return a; } else{ ls(b)=merge(a,ls(b)); update(b);return b; } } inline int new_node(int x){ sze[++cnt]=1; val[cnt]=x; rnd[cnt]=rand(); return cnt; } inline int find(int id,int k){//返回的以id为根的树的第k个数的位置 while(true){ if(k<=sze[ls(id)]) id=ls(id); else if(k==sze[ls(id)]+1) return id; else k-=sze[ls(id)]+1,id=rs(id); } } inline void insert(int val){ split(root,val,x,y); root=merge(merge(x,new_node(val)),y); } inline void delet(int val){ split(root,val,x,z); split(x,val-1,x,y); y=merge(ls(y),rs(y)); root=merge(merge(x,y),z); } inline void query_rank(int val){ split(root,val-1,x,y); print(sze[x]+1); root=merge(x,y); } inline void query_value(int k){ print(val[find(root,k)]); } inline void query_pre(int value){ split(root,value-1,x,y); print(val[find(x,sze[x])]); root=merge(x,y); } inline void query_suf(int value){ split(root,value,x,y); print(val[find(y,1)]); root=merge(x,y); } }Tree; signed main(void){ srand((unsigned)time(NULL)); int T=read(); while(T--){ int opt=read(),t=read(); switch(opt){ case 1: Tree.insert(t);break; case 2: Tree.delet(t);break; case 3: Tree.query_rank(t);break; case 4: Tree.query_value(t);break; case 5: Tree.query_pre(t);break; case 6: Tree.query_suf(t);break; } } return 0; }
5*.关于fhq-treap的可持久化
还没有学懂,后面再更新。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号