【字符串算法】一.哈希的应用

先疯狂安利 mzoj欢迎你
根据时间顺序，我将内容进行总结。
————————————————分割线————————————————

 一. Hash

众所周知，hash就一个字乱

 Hash，一般翻译做散列、杂凑，或音译为哈希，是把任意长度的输入（又叫做预映射pre-image）通过散列算法变换成固定长度的输出，该输出就是散列值。这种转换是一种压缩映射，也就是，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，所以不可能从散列值来确定唯一的输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。

上面是度娘~~瞎逼逼~~的官方，我们不要理会。

其实说白了，就是把字符串变成不同的数字，从而达到“独特”该串（我的理解）

比如有一个串"abc",而其对应的ASCII码就将每一个字符区分。
但其子串的hash值需另外定义。有一种简明扼要的定义方法（当然不是所有hash都这样定义，hash越乱越好）：

hash[i]=(hash[i-1]*base+s[i])%mod;

很容易看懂的伐，hash[i]指串的第i位的hash值；s[i]就是第i位的字符；base是一个常数一般取不是挺大的素数（我喜欢取997，1000以内最大的素数）；mod则是一个极大的素数，它规定了hash值的区间，一般可以取1e9+7或1e9+9，但太常用了以至于这两个数经常被卡，可以试试自己找一个自己喜欢的大素数。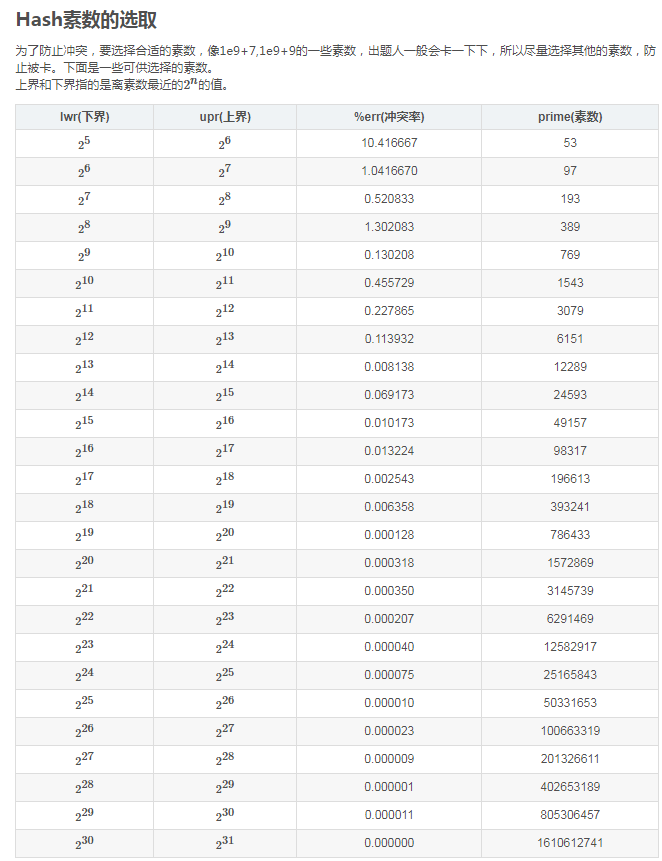


其实我更喜欢用unsigned long long让数值自溢达到mod的效果。

unsigned long long hash[maxn];
---------
hash[i]=hash[i-1]*base+s[i];

看个经典经典经典的例题hdu1386

（当然p3370是板子）
这个题是个hash（KMP)的模版题，在每一个字符的hash值求到以后，要求一个区间的hash值，怎么办呢？

丑的一批，不是重点我们找一下规律：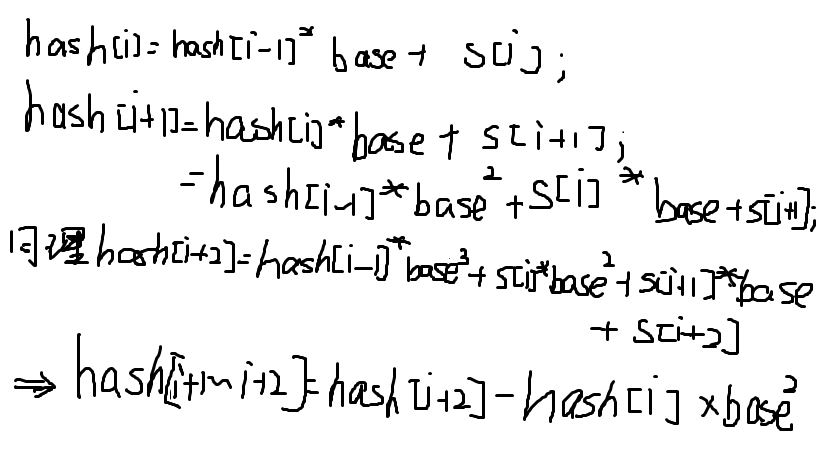
再手推一下，就可以得到规律:

hash[l..r]=(hash[r]-hash[l-1]*(p^(r-l+1)))%mod

 

所以这个题的答案也很简单了，放代码：

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int maxn=1e6+5;
const int base=997;
unsigned long long p[maxn],f[maxn],s,T,ans;
char s1[maxn],s2[maxn];
int main(){
    p[0]=1;
    for(int i=1;i<=maxn;i++)    p[i]=p[i-1]*base;
    cin>>T;
    while(T--){
        ans=s=0;
        scanf("%s%s",s1+1,s2+1);
        int l1=strlen(s1+1),l2=strlen(s2+1);
        for(int i=1;i<=l1;i++)    s=s*base+(unsigned long long)s1[i];
        for(int i=1;i<=l2;i++)    f[i]=f[i-1]*base+(unsigned long long)s2[i];
        for(int i=l1;i<=l2;i++)
            if(s==f[i]-f[i-l1]*p[l1])    ans++;
        cout<<ans<<endl;
    }
    return 0;
}

接下来有一个问题，假设我们的mod值取得是1e9+9，但这里有1e9+10和1，就是说这两个数最后取模的数相同，会发生冲突。怎么办呢？
下面有几个办法：

1.把mod值调的更大，而且选取素数。一般来说，mod的约数越多，冲突的几率越大。

2.基数转换法。把mod看作另一个进制的的数，再转回十进制。如十三进制中236075=2 * 13^5+3 * 13^4+6 * 13^3+7 * 13 + 5=十进制的841547。

3.常用的双哈希，当然还有3哈希，4哈希，但也不必了。

再推荐一道题p4656