第九讲-数列收敛的判定方法
本讲介绍了在不知的、复杂的、数列是否有极限(收敛)时,如何判断该数列收敛(有极限)的三种方法(夹逼定理(左右)、单调有界原理(单上、单下)、区间套)
夹逼定理
在直接考虑数列 极限的存在性或计算该数列的极限遇到困难时,可以采用放缩的方法,构造两个极限比较容易计算的数列,通过考虑它们的极限来得到所需的结果. 这就是夹逼定理,或称为三明治定理.
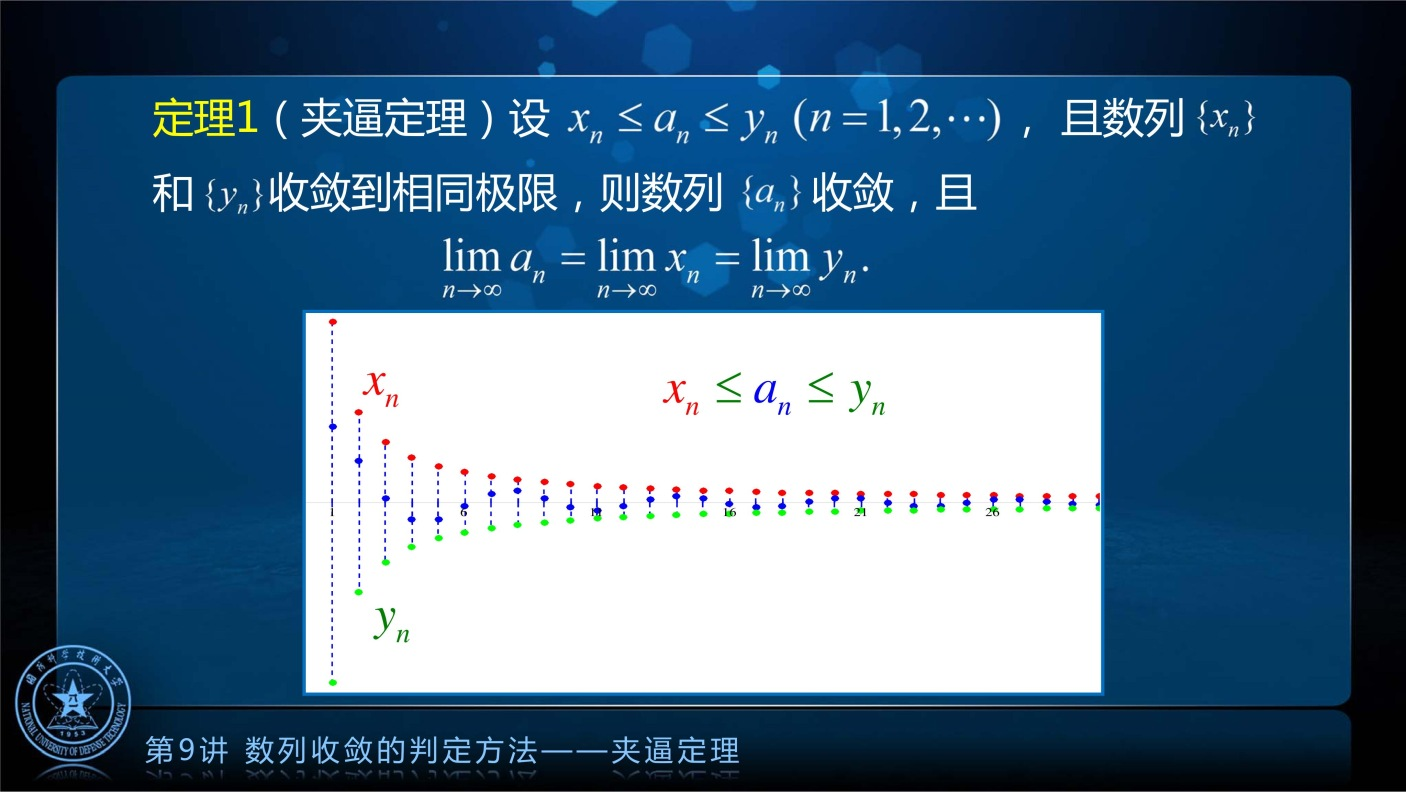
定理证明
证明:

定理应用
例 1. 证明: ![]()
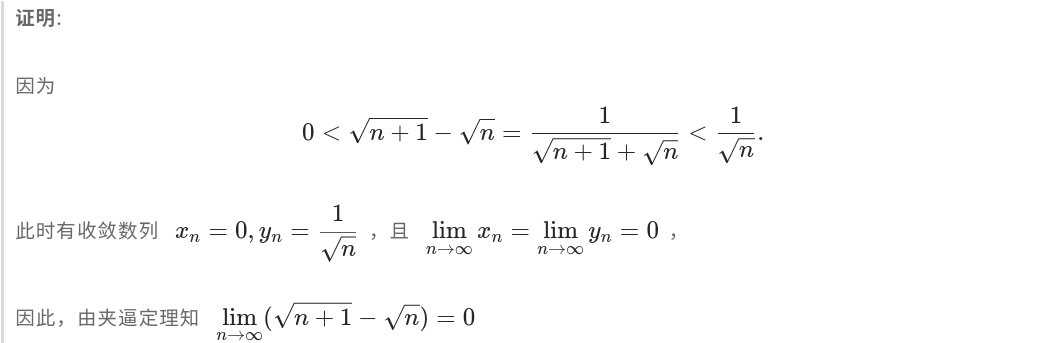

例 2. 求极限: ![]()

为什么不能用四则运算拆分?因为四则运算是有限项


牛皮
单调有界原理
任何单调有界数列一定存在极限.
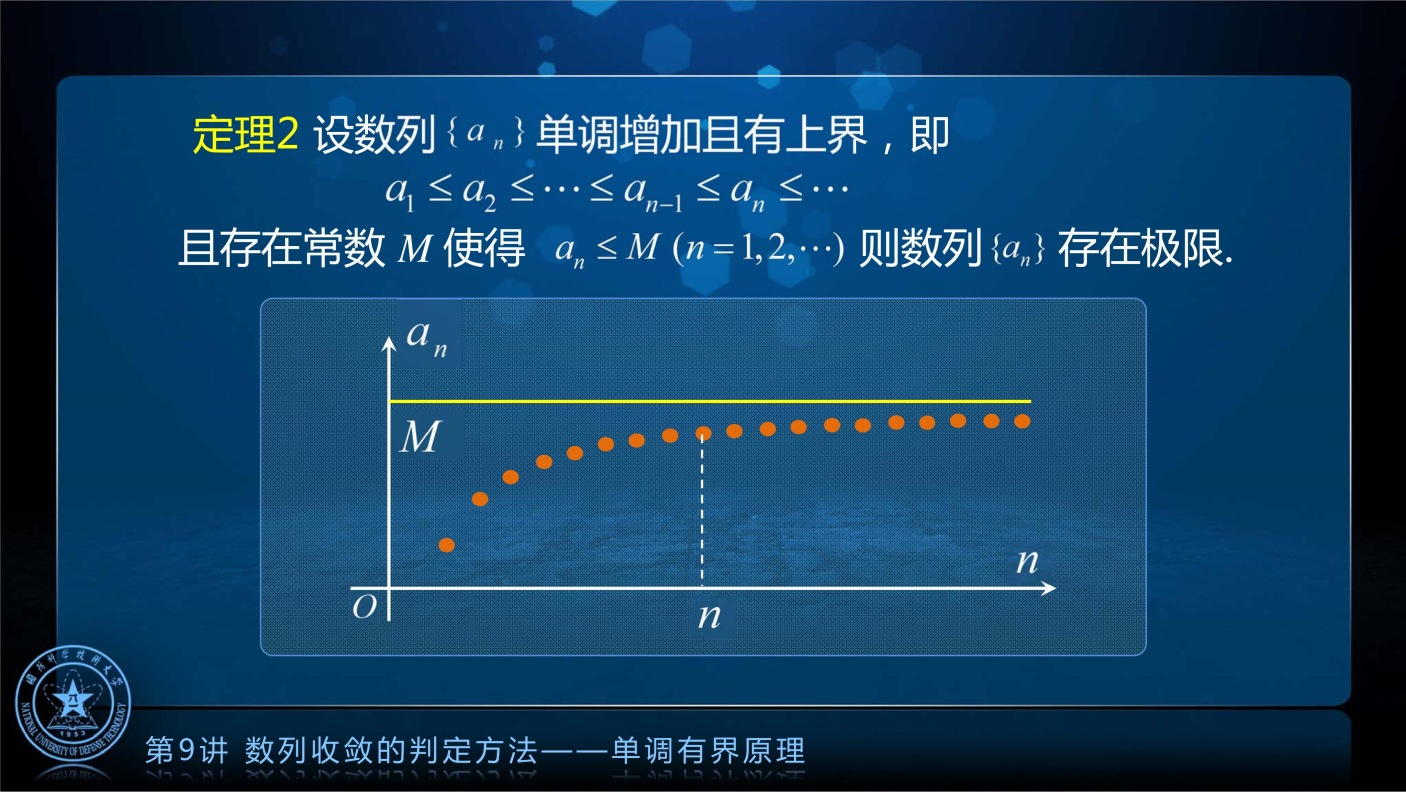
连续性公理
概念: 若一个实数集合存在上界,则它一定存在上确界. 集合 A 的上确界表示为 supA.
最小上确界
概念: 所谓一个函数集合 A 的上确界 a,是说 a 为该集合的最小上界. 这里包含两层意思,
- a 为 A 的上界,即对于任何 x∈A,有 x≤ a.
- 任何小于 a 的数都不可能构成 A 的上界,即对于任何正数 ε,一定存在 x′∈A,使 x′>a−ε (因为 a−ε 是小于 a 的数)
定理证明

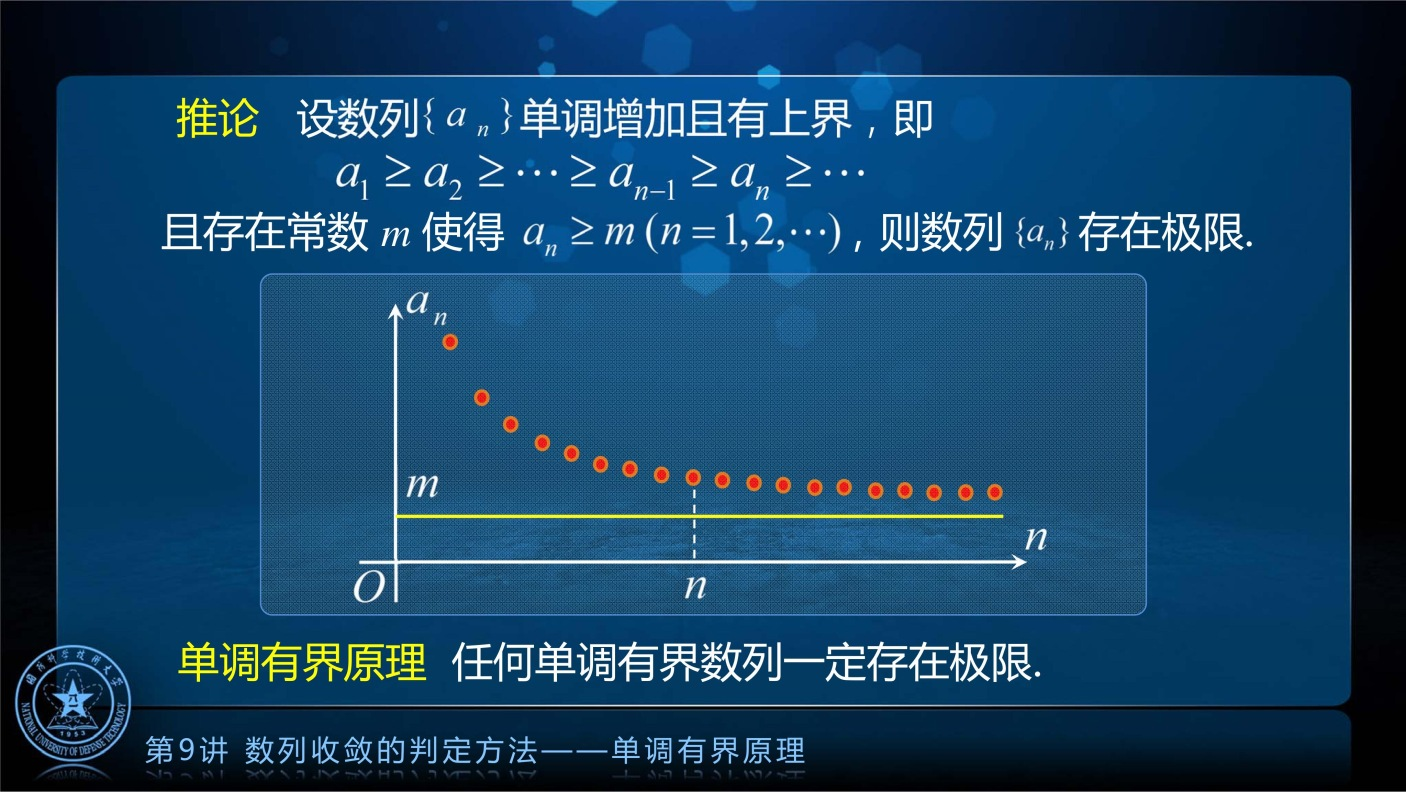
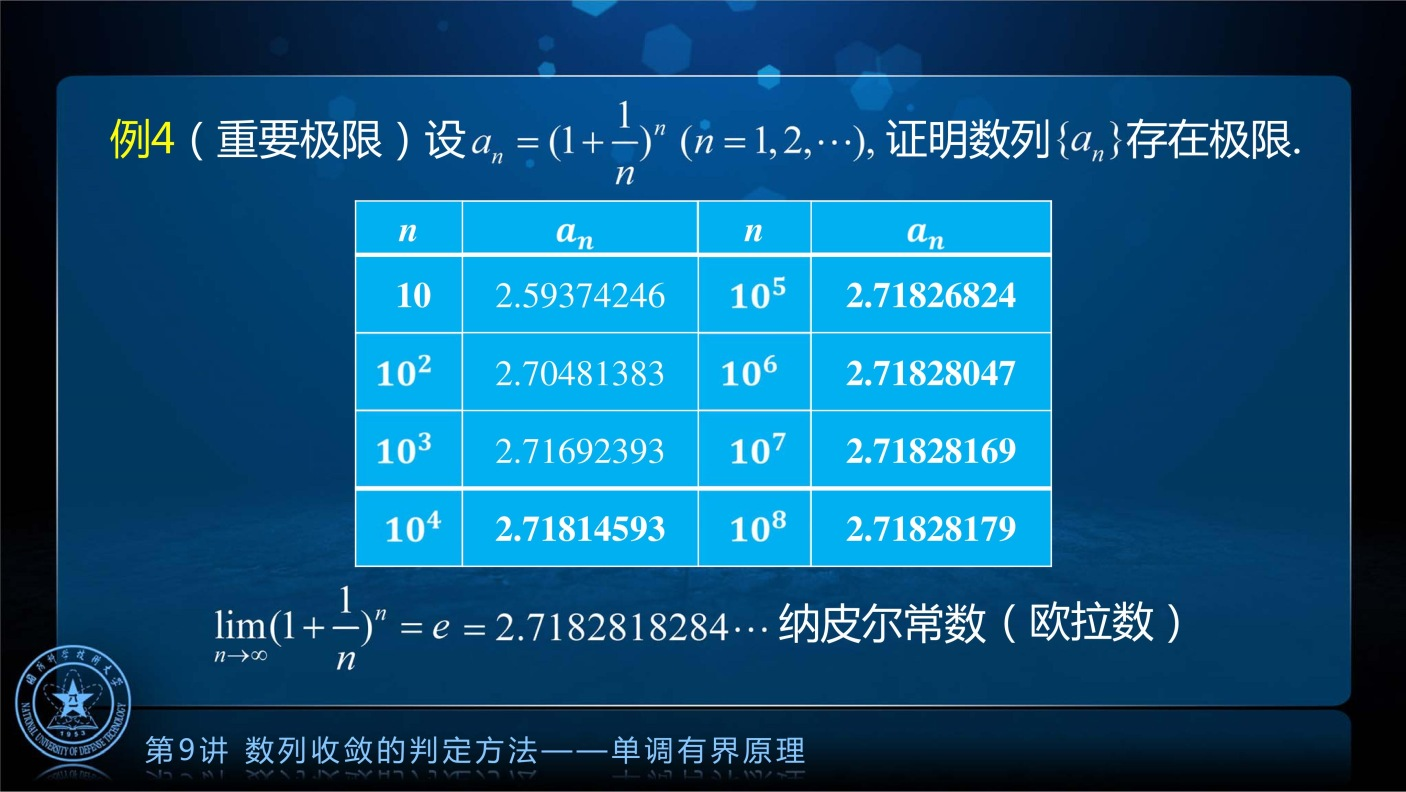
定理应用


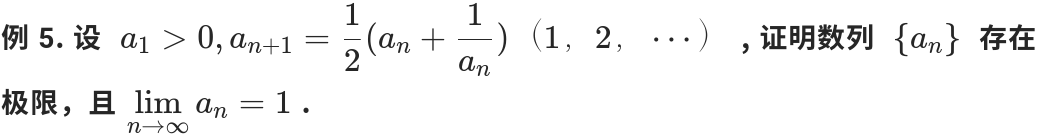
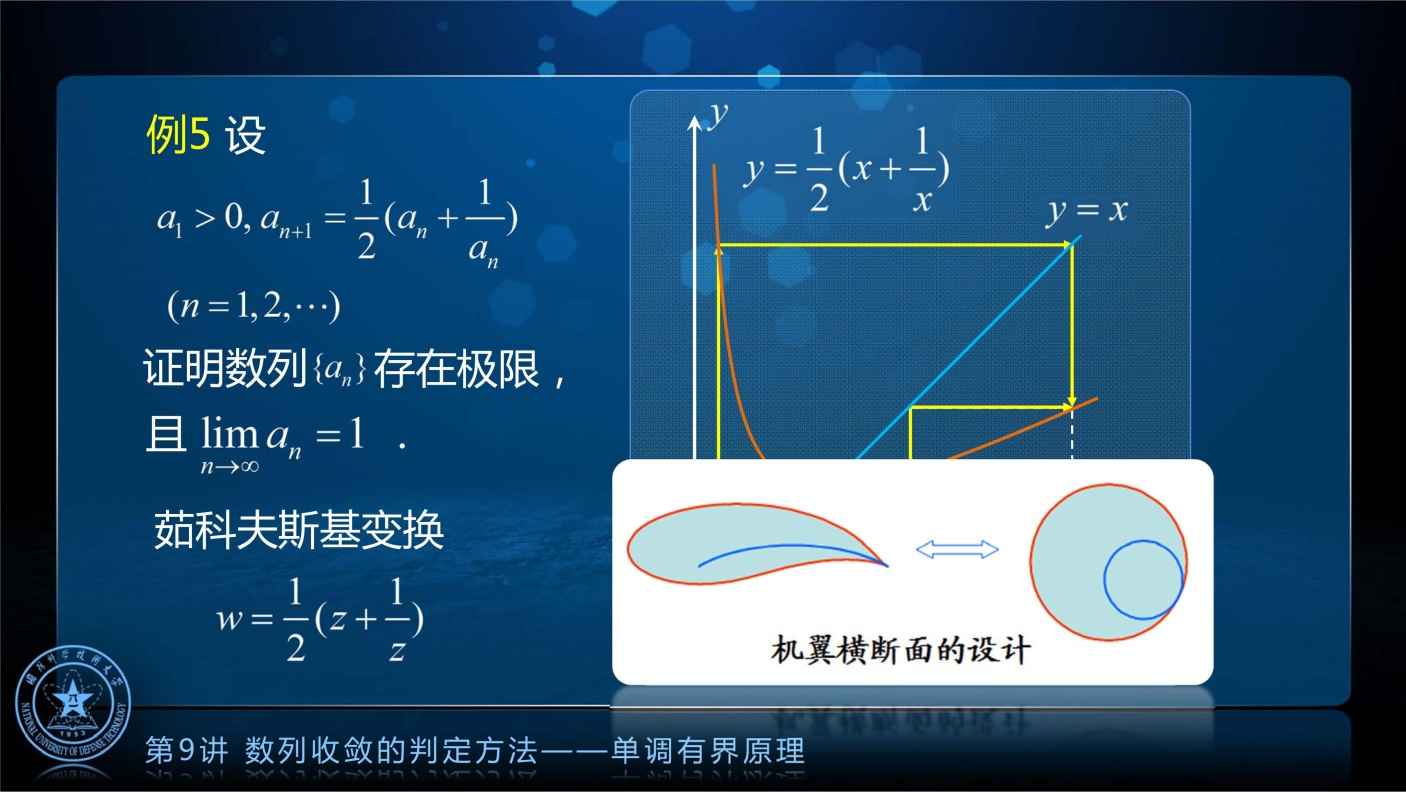

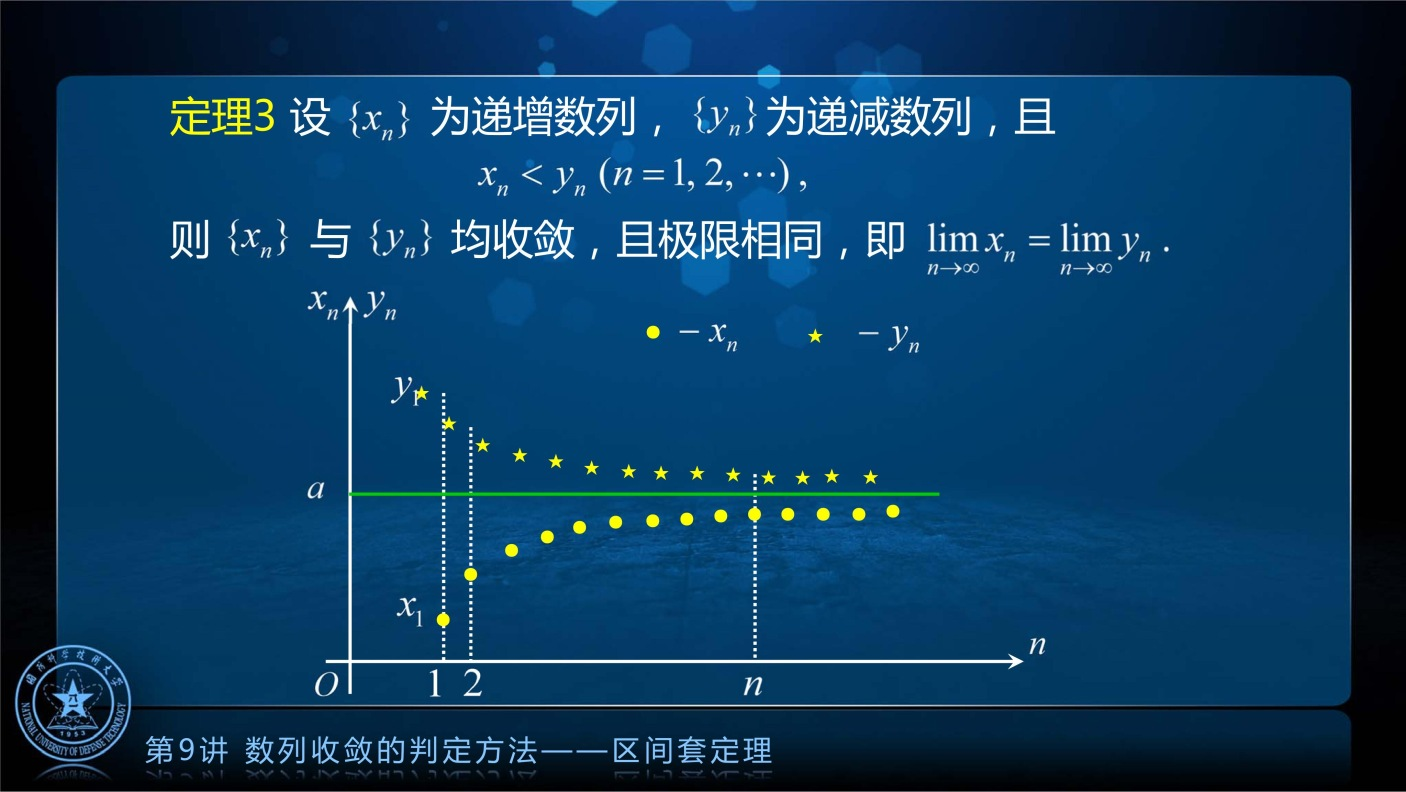
区间套定理



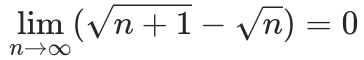
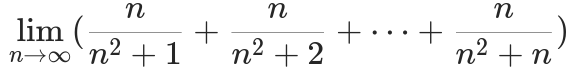
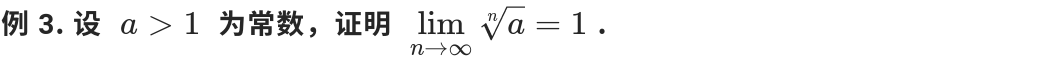
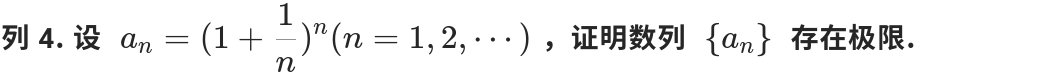

 浙公网安备 33010602011771号
浙公网安备 33010602011771号