第八讲-数列极限的性质
本讲介绍了极限的基本性质：数列的极限存在，极限唯一，数列有界，数列保号（n>N，an和极限同号）
数列极限的基本性质
定理 1: 唯一性
如果数列存在极限的话, 极限一定是唯一的. 也就是说, 如果同一个数列都存在极限, 且它们的极限分别为 a 和b 的话, a 和b一定相等, 这就是数列极限的唯一性.
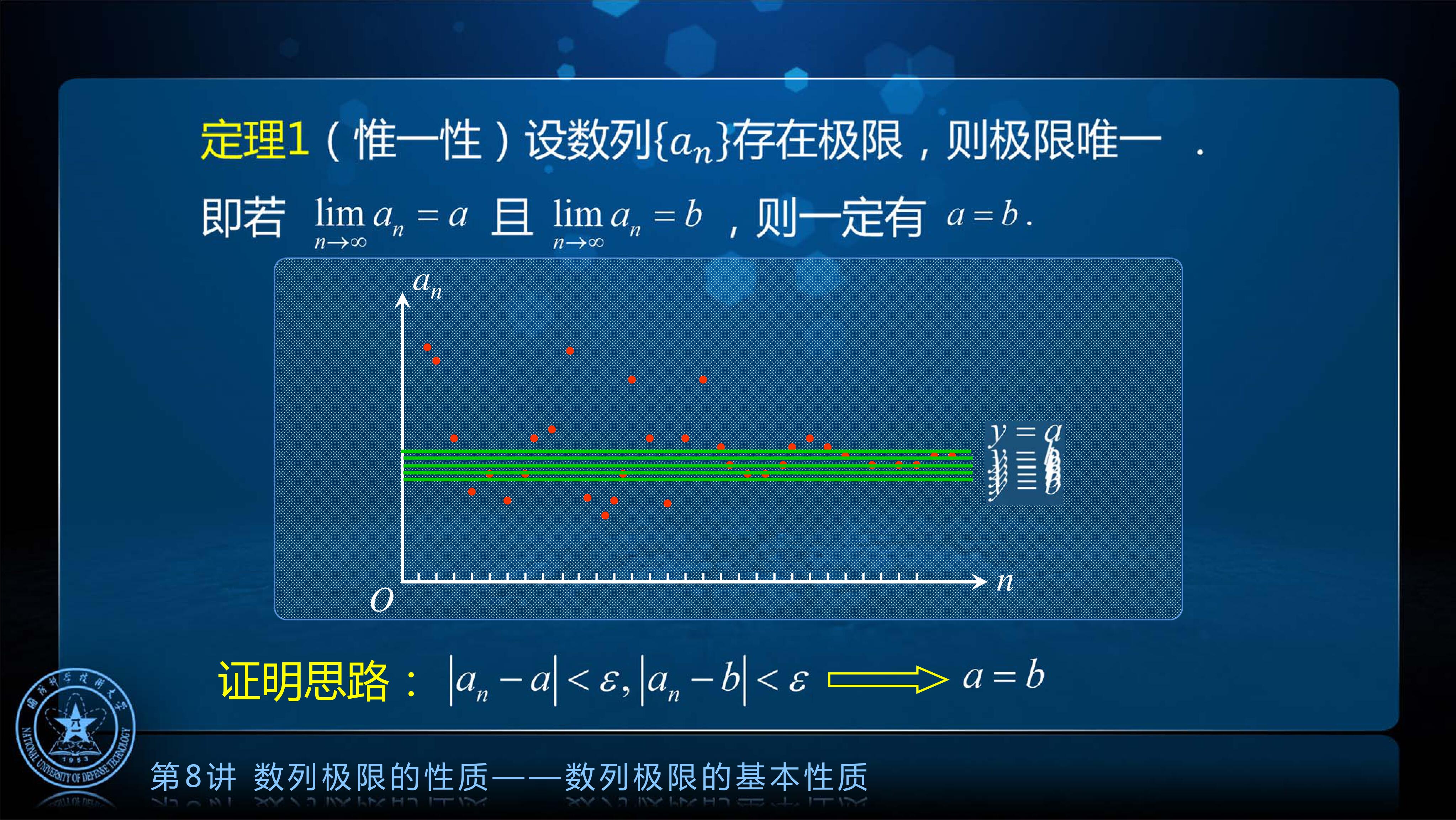
唯一性的证明(反证法):
设 , 取
, 由于
,
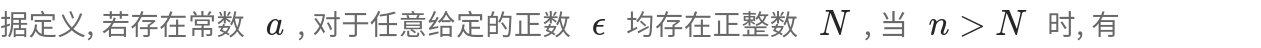
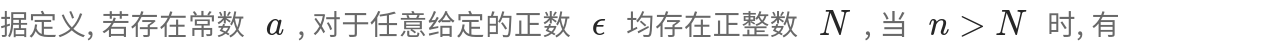
所以,
显然, 这里矛盾, 因此有 a=b.
定理 2: 有界性
如果数列 存在极限, 那
的绝对值一定小于某一个正的常数
.
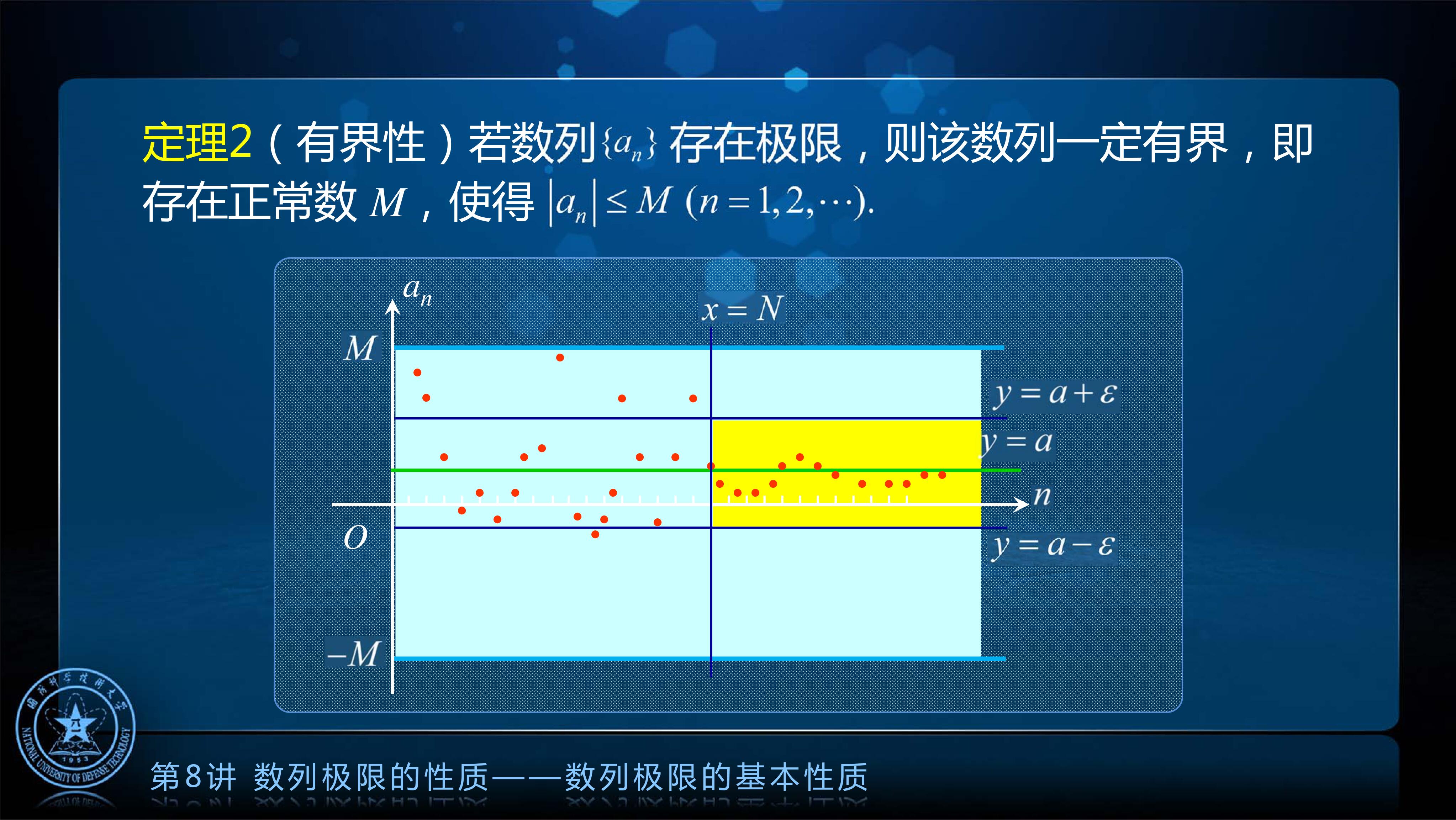
有界性的证明:
取 
时, 有,
取 , 则
定理 3: 保号性
如果一个数列存在极限, 而且极限是大于零的, 那么这个数列从某一项开始, 以后所有的项都是大于零的. 当极限小于零时结论相反.
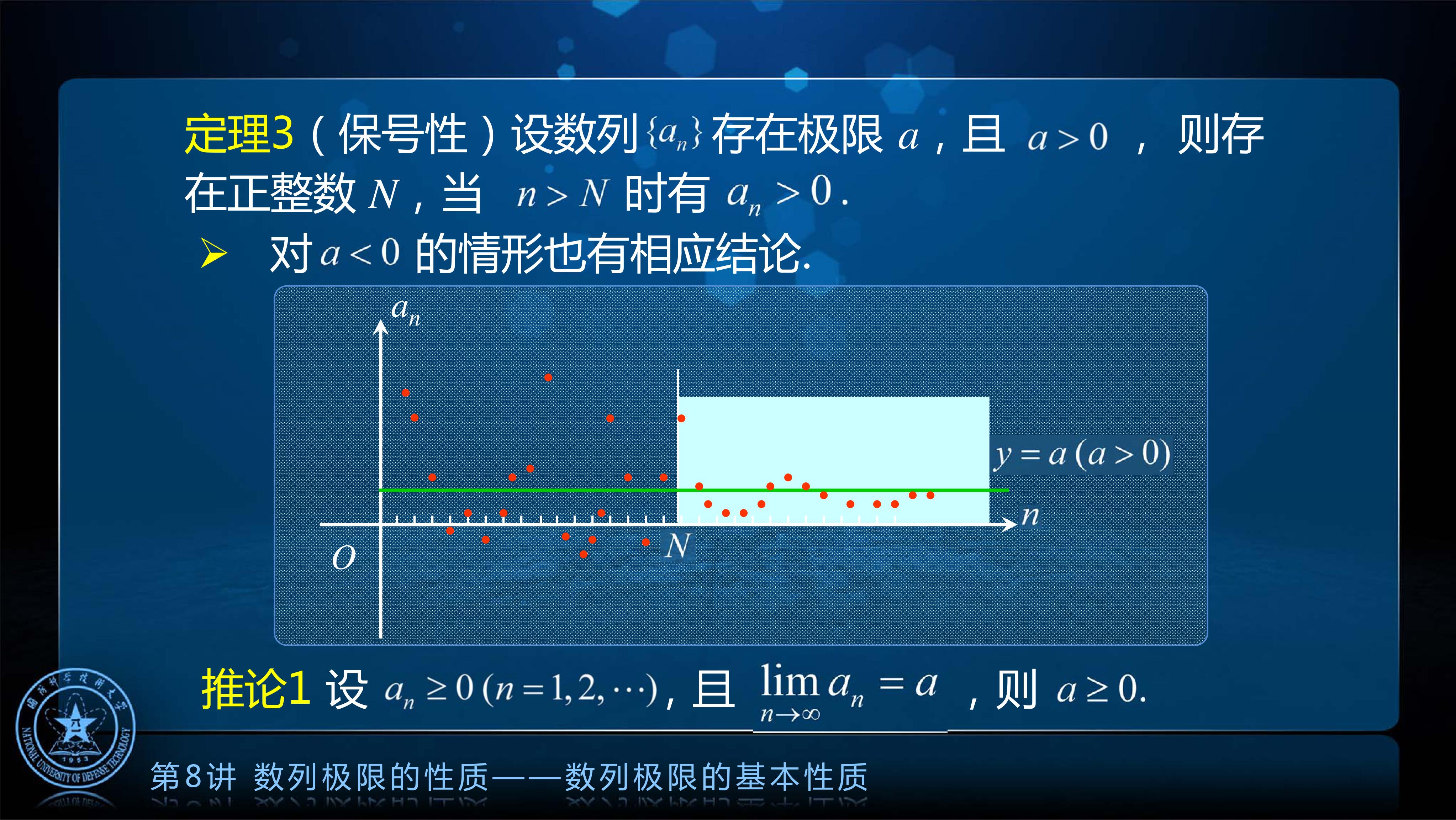
保号性的证明:
取 
, 当 n>N时,有,
得 .
推论是有定理往往很快可以得到的结论。
推论1：证L:举反例，当a<0,有定理3必可得到那么这个数列从某一项开始, 以后所有的项都是小于零的. 矛盾，证毕。
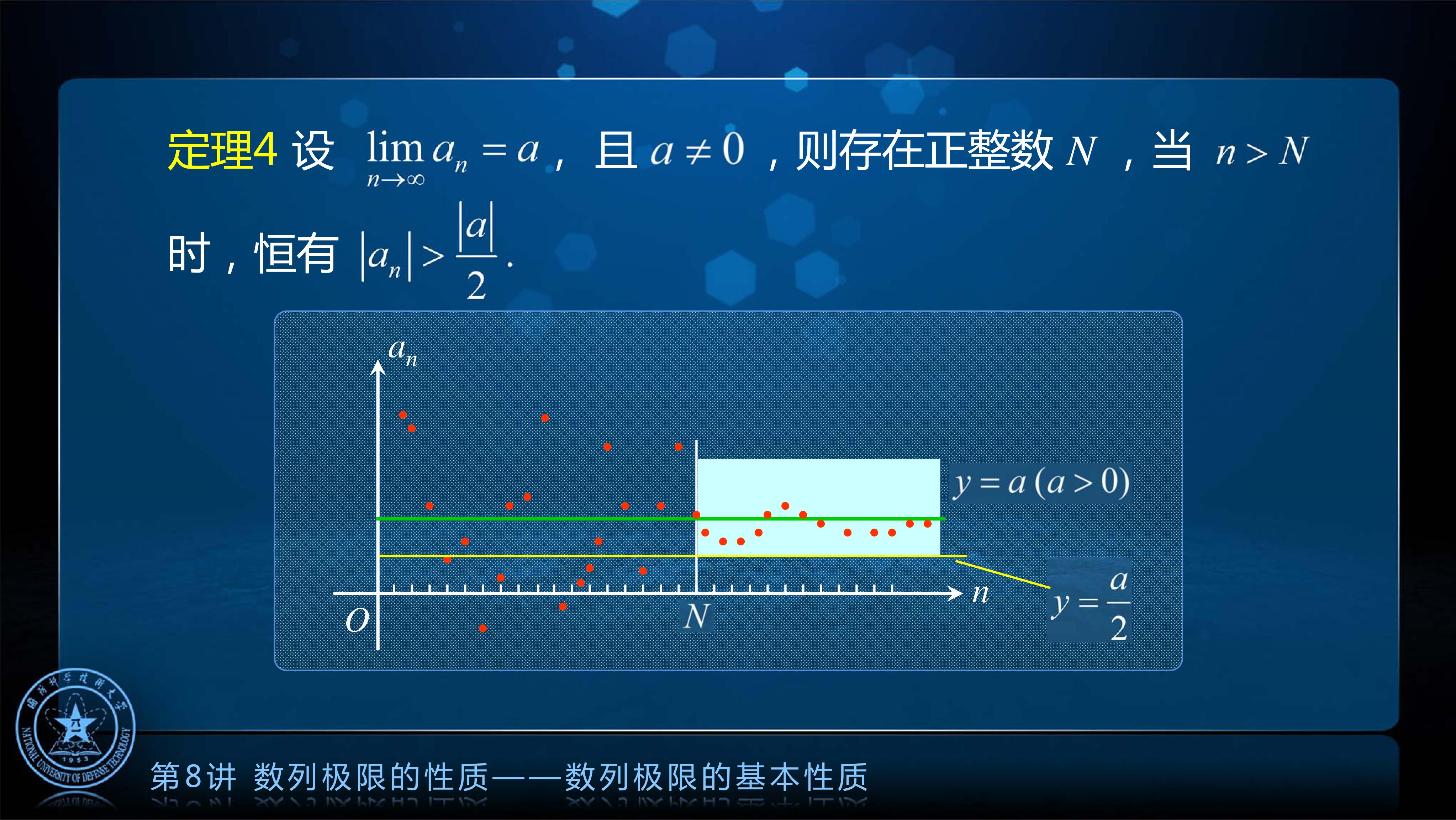
证明:
取 
, 当 n>N 时, 有,
推论2（定理4的证明结果的放大大）
数列极限的运算法则
极限的四则运算法则
两个数列相乘极限存在，这两个数列不一定极限存在，比如说两个(-1)n
例 1
k必须等于l?
例 2
思考解答同上
解:
令 , 得
所以, 和
的极限存在且极限值分别为 2 和 -1.
