MySQL 2 索引
█ 1. 索引底层数据结构
uuid是无序的。
B+解决了回旋 拿后面数据的问题
非叶子节点上 只有key,,叶子节点上有key value。
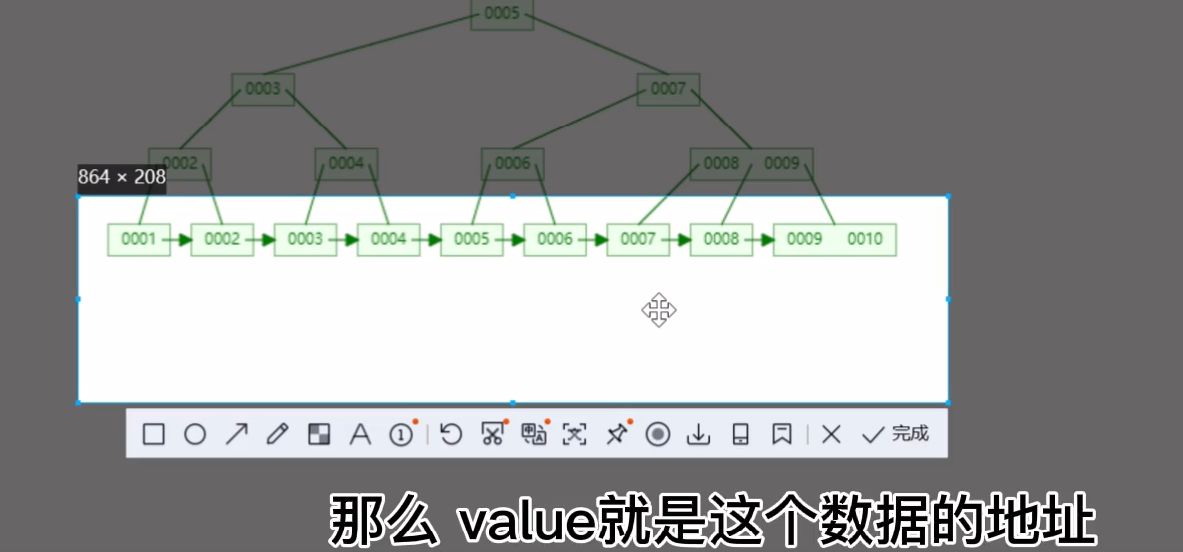
█ 2. 索引 代码



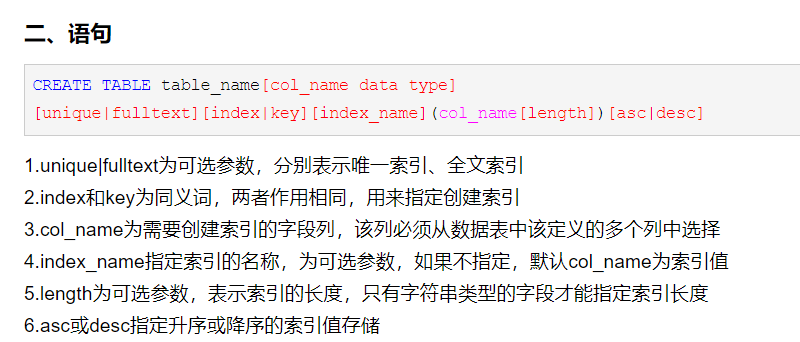
创建一:create [unique] index indexName on tableName (columnName (length) )。
如果是CHAR,VARCHAR类型,length可以小于字段实际长度;如果是 BLOB和TEXT类型,必须指定length。
创建二:alter tableName add [unique] index [indexName] on (columnName (length) )
删除:DROP INDEX [indexName] ON mytable;
查看:SHOW INDEX FROM table_name\G

alter table article add fulltext index idx_full_keyword(keywords);

实例:
// 建表
CREATE TABLE IF NOT EXISTS staffs(
id INT PRIMARY KEY AUTO_INCREMENT,
name VARCHAR(24) NOT NULL DEFAULT "" COMMENT'姓名',
age INT NOT NULL DEFAULT 0 COMMENT'年龄',
pos VARCHAR(20) NOT NULL DEFAULT "" COMMENT'职位',
add_time TIMESTAMP NOT NULL DEFAULT CURRENT_TIMESTAMP COMMENT'入职事件'
) CHARSET utf8 COMMENT'员工记录表';
// 插入数据
INSERT INTO `test`.`staffs` (`name`, `age`, `pos`, `add_time`) VALUES ('z3', 22, 'manager', now());
INSERT INTO `test`.`staffs` (`name`, `age`, `pos`, `add_time`) VALUES ('July', 23, 'dev', now());
INSERT INTO `test`.`staffs` (`name`, `age`, `pos`, `add_time`) VALUES ('2000', 23, 'dev', now());
// 建立复合索引(即一个索引包含多个字段)
ALTER TABLE staffs ADD INDEX idx_staffs_nameAgePos(name, age, pos);
○ 2.1 索引的种类

○ 2.2 索引的分类

○ 2.3 哪些情况需要建索引

█ 3. 数据库是如何通过索引定位数据
█ 3. MySQL两大引擎MyIsam和InnoDB
○ 3.1 聚簇索引 和 非聚簇索引

○ 3.2 MyIsam 和 InnoDB 区别


○ 3.3 MyIsam 查询流程 InnoDB
3.3.1 MyIsam 查询流程

3.3.2 InnoDB 查询流程


!!!innodb支持全文索引是从mysql5.6开始的
█ 4. MySQL性能优化 索引失效
联合索引 会存在失效问题
○ 4.0 最左前缀法则
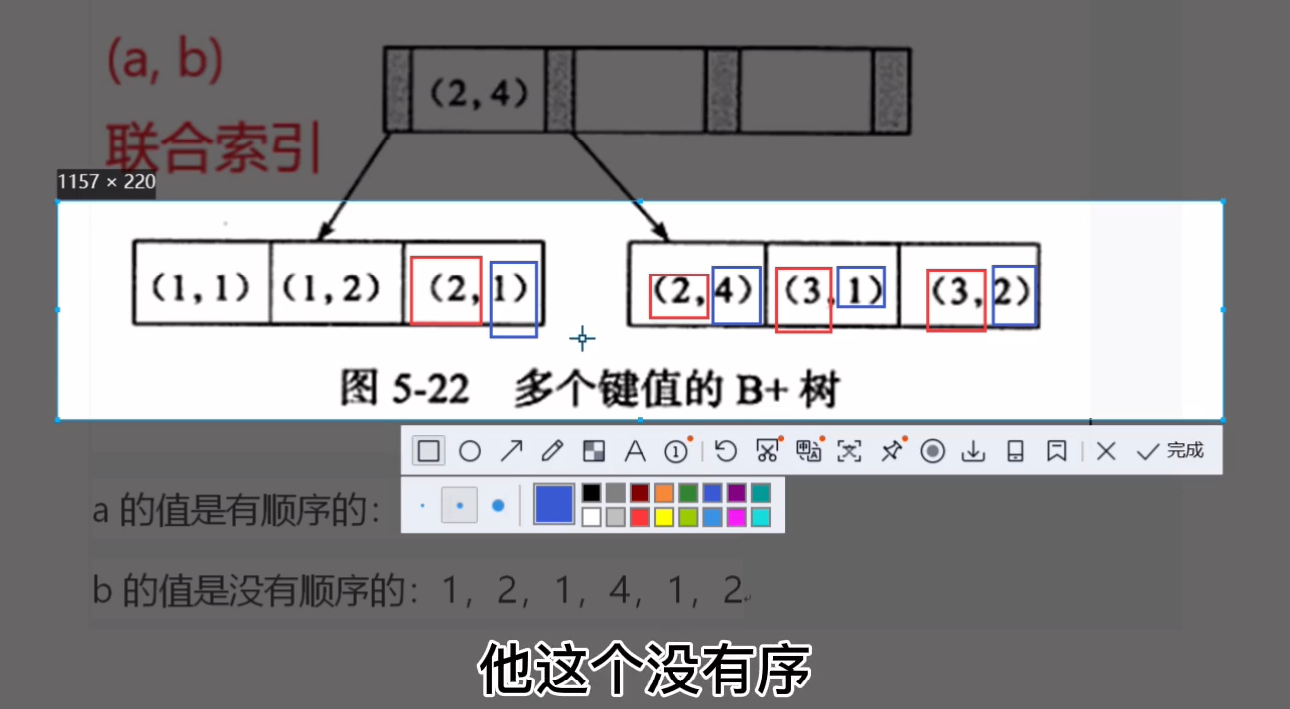
a->b->c

联合索引

○ 4.1 AND 是可以用到索引的 OR后面的不可以

○ 4.2 不要对索引做以下处理

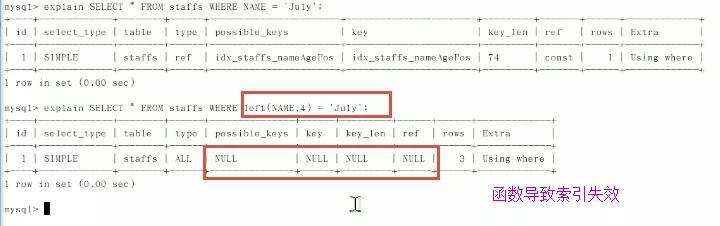
○ 4.3 索引不要放在范围查询右边
原因
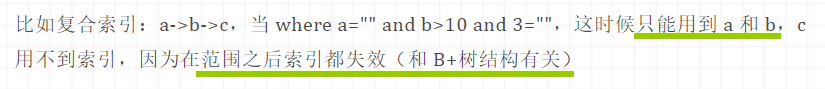
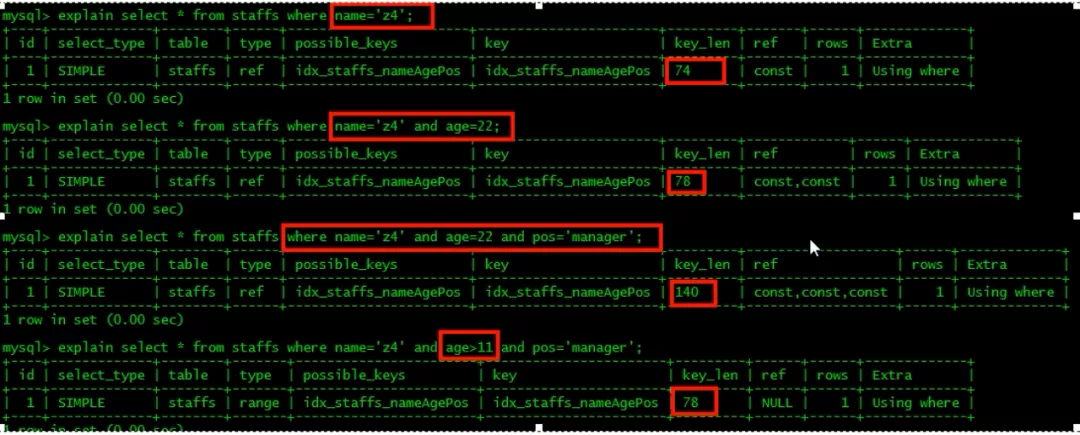
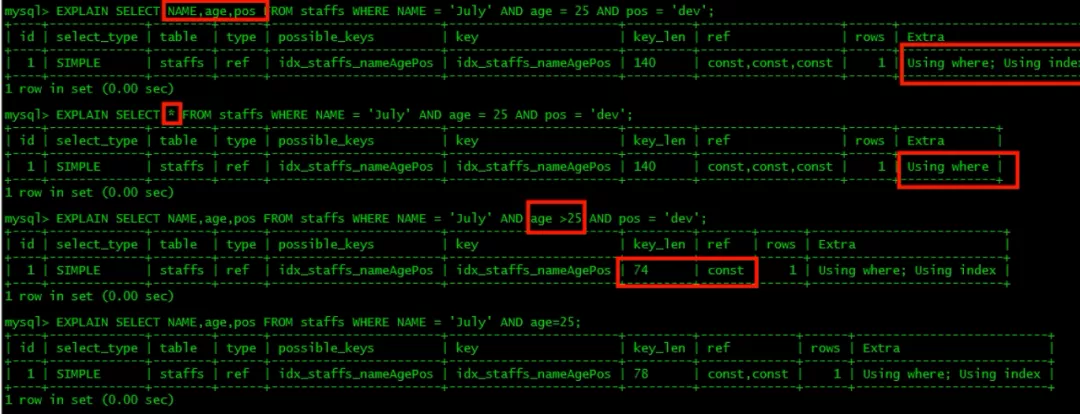
○ 4.4 减少 select * 的使用
同样的查询 这几个字段,select 字段名<覆盖索引> 是明确用到index的;
单独的select* 显示的using where
○ 4.5 like 模糊搜索 覆盖索引
原因:

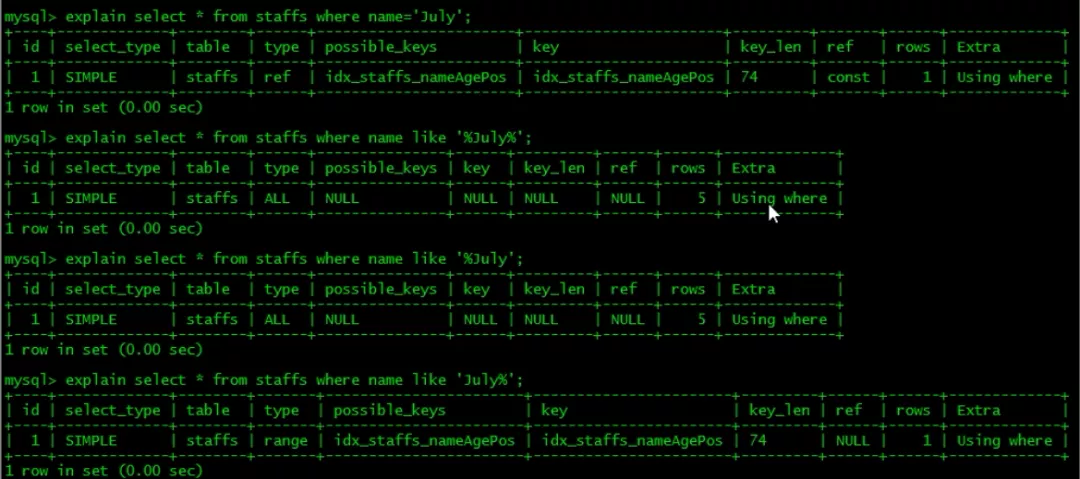

%% 执行时间慢,虽然不显示 但是用到了覆盖索引,用到了索引。
○ 4.6 order by 优化


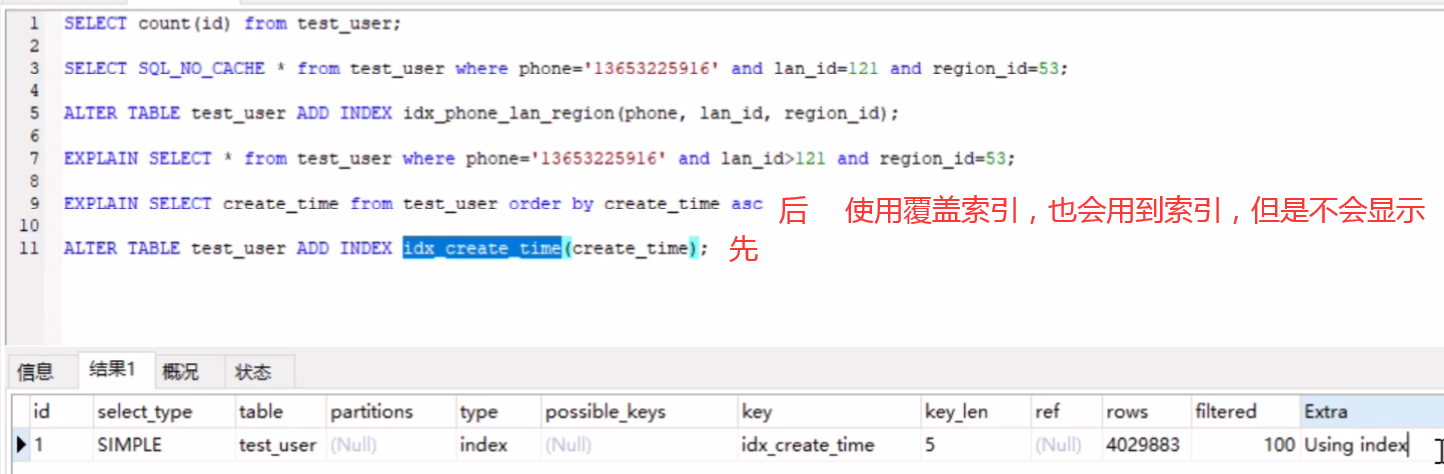
order by 排序算法
双路排序 单路排序




○ 4.8 group by

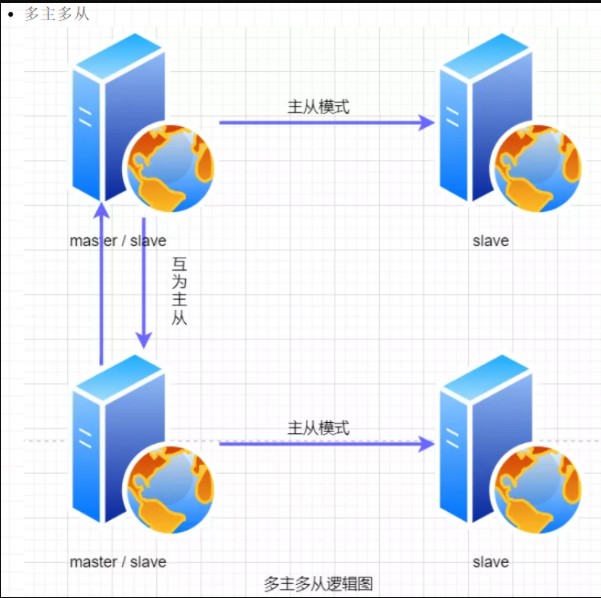
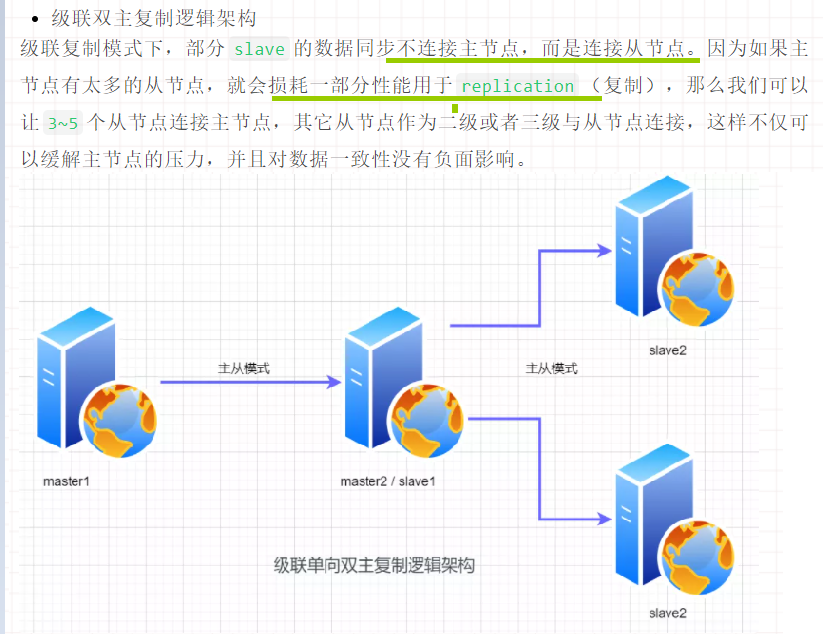
█ 5. MySQL优化--- 主从复制


master slave
单向主从 // 一主多从 // 互为主从 // 多主多从 // 级联双主复制逻辑架构


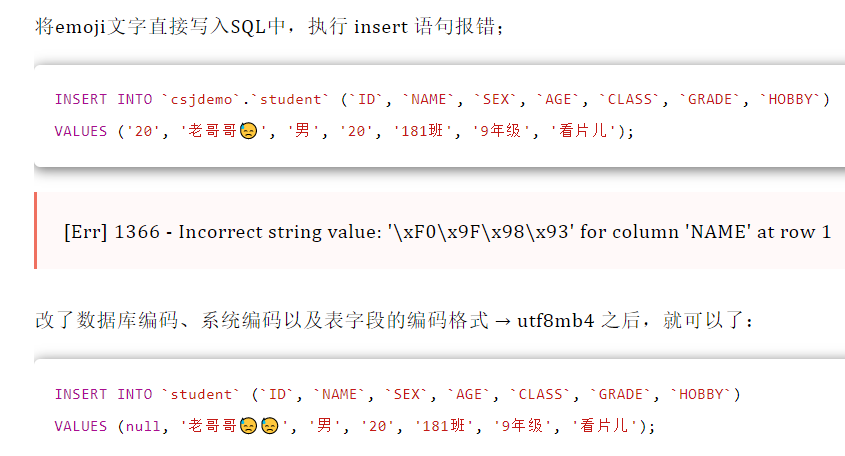
█ 6. UTF-8 utf8mb4
MySQL 的“utf8mb4”才是真正的“UTF-8”。




█ 9.索引 B+树
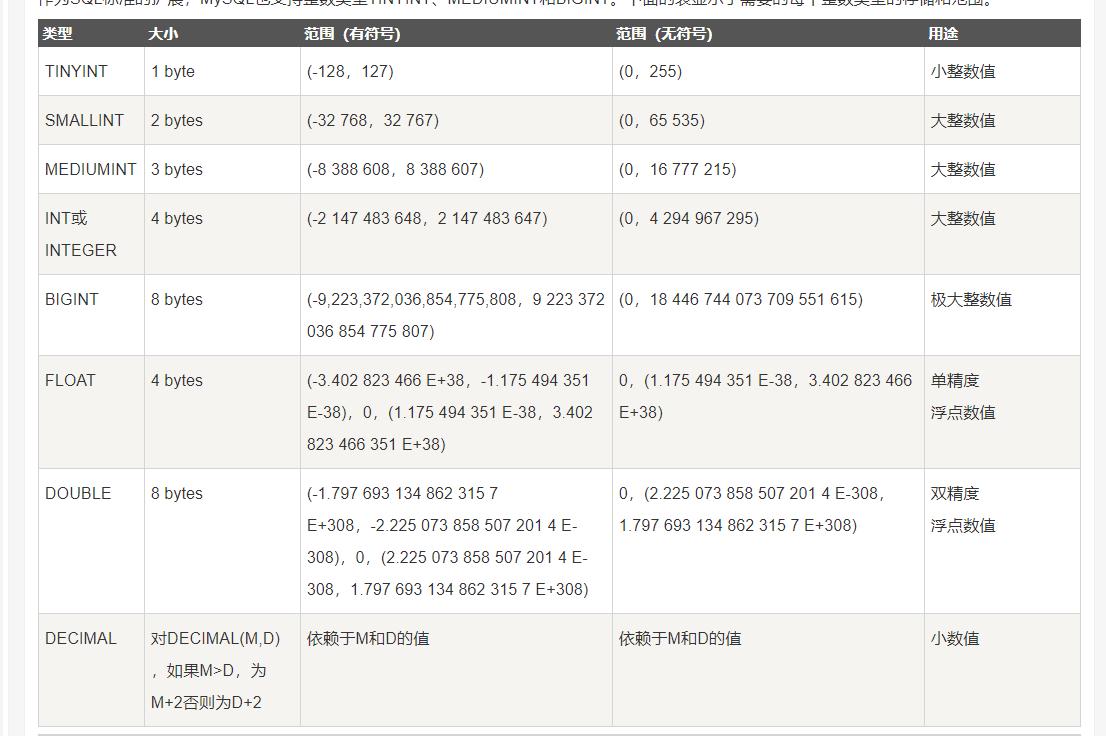
Mysql的索引
索引的目的在于提高查询效率
B+树索引(O(log(n))) B-Tree索引 Hash索引

○ 9.1 B+树的实现
多路搜索树
1)有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点。
2)所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
3)所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素
4)B+树的搜索与 B 树也基本相同,区别是 B+树只有达到叶子结点才命中(B 树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
5)所有关键字都出现在叶子结点的链表中(即数据只能在叶子节点【也叫稠密索引】),且链表中的关键字(数据)
恰好是有序的。
6)非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层
○ 9.2为什么使用B+树:
索引查找过程中就要产生磁盘I/O消耗,主要看IO次数,和磁盘存取原理有关。
根据B-Tree的定义,可知检索一次最多需要访问h个节点。
数据库系统的设计者巧妙利用了磁盘预读原理,
将一个节点的大小设为等于一个页,这样每个节点只需要一次I/O就可以完全载入

○ 9.3 索引的底层实现(B+树,为何不采用红黑树,B树)重点
| 树 | 区别 |
|---|---|
| 红黑树 | 增加,删除,红黑树会进行频繁的调整,来保证红黑树的性质,浪费时间 |
| B树也就是B-树 | B树,查询性能不稳定,查询结果高度不致,每个结点保存指向真实数据的指针,相比B+树每一层每屋存储的元素更多,显得更高一点。 |
| B+树 | B+树相比较于另外两种树,显得更矮更宽,查询层次更浅 |
█ 10.树
○ 10.1 B树 2-3树:
B树:Balanced
1)B 树通过重新组织节点, 降低了树的高度.
2)文件系统及数据库系统的设计者利用了磁盘预读原理,将一个节点的大小设为等于一个页(页得大小通常为4k), 这样每个节点只需要一次 I/O 就可以完全载入
3)将树的度 M 设置为 1024,在 600 亿个元素中最多只需要 4 次 I/O 操作就可以读取到想要的元素,B 树(B+)广泛应用于文件存储系统以及数据库系统中
B树的特点
1)B 树的阶:节点的最多子节点个数。比如 2-3 树的阶是 3,2-3-4 树的阶是 4;
2)B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找;
3)关键字集合分布在整颗树中, 即叶子节点和非叶子节点都存放数据.
2-3树:
1)2-3 树的所有叶子节点都在同一层.(只要是 B 树都满足这个条件)
2)有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点.
3)有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点
4)当按照规则插入一个数到某个节点时,不能满足上面三个要求,就需要拆,先向上拆,如果上层满,则拆本层, 拆后仍然需要满足上面 3 个条件。
5)对于三节点的子树的值大小仍然遵守(BST 二叉排序树)的规则
○ 10.2 B+ 多路搜索树
1)有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点。
2)所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
3)所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素
4)B+树的搜索与 B 树也基本相同,区别是 B+树只有达到叶子结点才命中(B 树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
5)所有关键字都出现在叶子结点的链表中(即数据只能在叶子节点【也叫稠密索引】),且链表中的关键字(数据)
恰好是有序的。
6)非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层
○ 10.3 B*树
在 B+树的非根和非叶子结点再增加指向兄弟的指针。
1)B树定义了非叶子结点关键字个数至少为(2/3)M,即块的最低使用率为 2/3,而 B+树的块的最低使用率为的 1/2。
2)从第 1 个特点我们可以看出,B*树分配新结点的概率比 B+树要低,空间使用率更高
○ 10.4 红黑树
特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
红黑树的特性:
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
注意:
(01) 特性(3)中的叶子节点,是只为空(NIL或null)的节点。
(02) 特性(5),确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对是接近平衡的二叉树。
应用:
主要是用它来存储有序的数据,它的时间复杂度是O(lgn),效率非常之高。
例如,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
○ 10.5 霍夫曼树
又称为最优二叉树,其主要作用在于数据压缩和编码长度的优化。
给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为霍夫曼树(Huffman Tree)。


