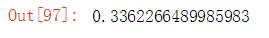经典算法之K近邻(回归部分)
1.算法原理
1.分类和回归
分类模型和回归模型本质一样,分类模型是将回归模型的输出离散化。
一般来说,回归问题通常是用来预测一个值,如预测房价、未来的天气情况等等,例如一个产品的实际价格为500元,通过回归分析预测值为499元,我们认为这是一个比较好的回归分析。回归是对真实值的一种逼近预测。
分类问题是用于将事物打上一个标签,通常结果为离散值。例如判断一幅图片上的动物是一只猫还是一只狗。分类并没有逼近的概念,最终正确结果只有一个,错误的就是错误的,不会有相近的概念。
简言之:
定量输出称为回归,或者说是连续变量预测,预测明天的气温是多少度,这是一个回归任务
定性输出称为分类,或者说是离散变量预测,预测明天是阴、晴还是雨,就是一个分类任务
2.KNN回归
KNN算法不仅可以用于分类,还可以用于回归。通过找出一个样本的k个最近邻居,将这些邻居的某个(些)属性的平均值赋给该样本,就可以得到该样本对应属性的值。
3.原理
问题引入
不知道的话,就去看看别人3个卧室的房子都租多少钱吧!

其中,K代表我们的候选对象个数,也就是找和我房间数量最相近的K个房子的价格,做一定的处理后(例如平均),作为我们房子的出租价格。
那么,如何衡量和我的房子最相近呢?如何评估我们得到的出租价格的好坏呢?
K近邻原理
假设我们的数据源中只有5条信息,现在我想针对我的房子(只有一个房间)来定一个价格。

在这里假设我们选择的K=3,也就是选3个跟我最相近的房源。

再综合考虑这三个只有房子的价格,就得到了我的房子大概能值多钱啦!
如何才能知道哪些数据样本跟我最相近呢?
欧氏距离公式:

其中p1到pn是一条数据的所有特征信息,q1到qn是另一条数据的所有特征信息。
4.举例说明
假设我们的房子有3个房间
单变量下的距离定义简化为:

读取数据:
import pandas as pd features = ['accommodates','bedrooms','bathrooms','beds','price','minimum_nights','maximum_nights','number_of_reviews'] dc_listings = pd.read_csv('listings.csv') dc_listings = dc_listings[features] print(dc_listings.shape) dc_listings.head()
仅取以单个指标accommodates的个数来计算每个样本到我们的距离:
代码实现如下:
import numpy as np # 定义我们的accomodates个数为3 our_acc_value = 3 # 新增一列distance,记录每个样本到3的距离 # np.abs函数用于计算绝对值 # 通过dc_listings.accommodates取出accommodates列的所有数据 # 可通过dc_listings.accommodates取值 # 也可通过字典的形式取值,dc_listings['accommodates']或dc_listings.get('accommodates') dc_listings['distance'] = np.abs(dc_listings.accommodates - our_acc_value) # 取出结果列distance # value_counts()统计个数 # sort_index()按照索引distance排序 dc_listings.distance.value_counts().sort_index()
输出结果:
0 461
1 2294
2 503
3 279
4 35
5 73
6 17
7 22
8 7
9 12
10 2
11 4
12 6
13 8
Name: distance, dtype: int64
从结果中可以看出,以房间个数来衡量的话,同样有3个房间的样本一共461个
假设K=5,即取距离我们最近的五个样本的价格取平均值,作为我们的出租价格。
# 使用sample函数,进行洗牌操作,将数据随机打乱 # farc = 1 表示选择100%的数据 # random_stare-0 表示设置随机种子 dc_listings = dc_listings.sample(frac=1, random_state=0) # 以instance为索引,进行升序排序 dc_listings = dc_listings.sort_values('distance') # 取出价格列 price = dc_listings.price # 对价格进行一定的处理,去掉$和,两个符号,并转化为float类型dc_listings['price'] = price.str.replace(r'\$|,', '').astype(float) # 取K=5时,预测的出租价格 pre_price = dc_listings.price.iloc[:5].mean() print(pre_price)
得到了平均价格,也就是我们的房子大致的价格了。这个就是KNN回归预测的整个过程。这里仅做一个例子,旨在说明KNN回归的过程。
实际情况下,我们有很多个样本,而且每个样本不仅仅只有一个accomodate属性。
2.基于单变量预测价格
实际情况下,一般将样本划分为两部分,一部分用作训练(称之为训练集)用于训练模型;一部分用作测试(称之为测试集)对训练出的模型进行评估。

继续上面的数据进行演示,此时的数据长这个样子:

输入以下代码,构造训练集和测试集。
# 删除distance列, axis=1表示按列删除 dc_listings.drop('distance', axis=1) # 训练集,取前2792行作为训练集 df_train = dc_listings.copy().iloc[:2792] # 测试集,剩下的作为测试集 df_test = dc_listings.copy().iloc[2792:]
仅考虑accommodates一个衡量指标下,对测试集中的所有样本的价格进行预测,并与真实值进行对比。
def predict_price(new_listing_value, fea_col): """ 对房子出租价格进行预测,K取值5 new_listing_value : fea_col: 特征列,参考的特征 """ df_temp = df_train # 导入训练集数据 # 在df_temp中添加一列,用于记录距离 df_temp['distance'] = np.abs(df_train[fea_col] - new_listing_value) # 按照distance索引进行升序排序 df_temp = df_temp.sort_values('distance') # 取距离最近的前5行数据 KNN_5 = df_temp.price.iloc[:5] # 取平均值作为预测值 predict_price = KNN_5.mean() return predict_price
例如,上文中的预测accomodates为3的价格,那么fea_col = 'accomodates', new_listing_value=3;
那么,对于测试集中的样本,accomodates属性值(即new_listing_value)是不同的,使用apply函数,循环调用预测函数,并得到测试样本中每个样本的预测值。
# 取测试集中,每个样本的accomodates值 # 应用predice_price函数,得到预测值 # 并新增一列predict_price记录预测值 df_test['predict_price'] = df_test.accommodates.apply(predict_price, fea_col='accommodates') # 取出预测值与真实值这两列,对比 df_test[['predict_price', 'price']]
部分输出结果:
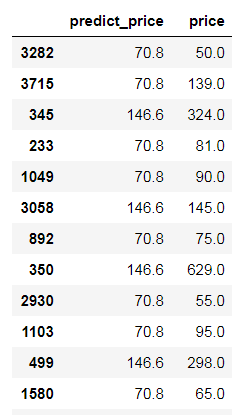
那么,如何评判预测结果的好坏呢?
3.误差评估
一般采用均方根误差(root mean squared error,RMSE)作为误差评估指标,误差越大,说明预测效果越差。
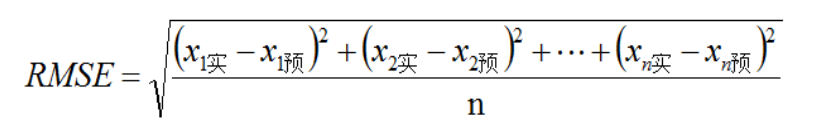
因此,基于上文内容,计算测试集总的均方根误差:
# 求出预测值与真实值差值的平方 df_test['squared_error'] = (df_test.predict_price - df_test.price)**2 # 求差值均值 mse = df_test.squared_error.mean() # 求均方差误差 rmse = mse ** (1/2) print(rmse)
如此,就得到了对于一个变量的模型评估分。
结果输出:

显然,此误差值较大,可见仅仅用一个指标,结果不一定靠谱。
那么,如何能降低这个预测的误差呢?显然需要利用多个指标对房子的价格进行评估。但是不同指标的单位不同,且相差较大。
因此,考虑将数据进行一定的处理,将所有数据都处理成不受单位影响的指标。
4.数据标准化与归一化
一般将数据进行标准化或归一化处理,使其不受单位影响。
z-score标准化
z-score标准化是将数据按比例缩放,使之落入一个特定区间。 要求:均值 μ = 0 ,σ = 1
标准差公式:
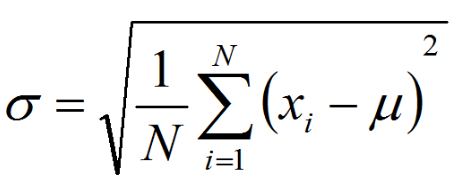
z-score标准化转换公式:

归一化
归一化:把数变为(0,1)之间的小数
归一化公式:
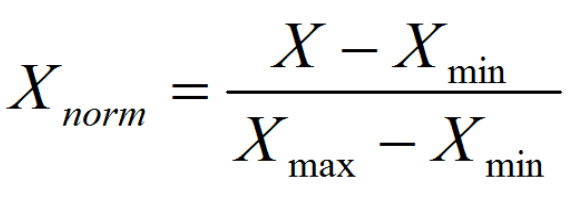
这里利用sklearn的MinMaxScaler和StandardScaler两个类,对所有数据进行归一化处理。
import pandas as pd from sklearn import preprocessing from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import StandardScaler # 读取数据 features = ['accommodates','bedrooms','bathrooms','beds','price','minimum_nights','maximum_nights','number_of_reviews'] dc_listings = pd.read_csv(r'D:\codes_jupyter\数据分析_learning\课件\05_K近邻\listings.csv', engine='python') dc_listings = dc_listings[features] # 对price列进行一定的处理,使其变成float型 dc_listings['price'] = dc_listings.price.str.replace(r'\$|,', '').astype(float) # 对缺失值进行处理,删除有缺失值的数据 dc_listings = dc_listings.dropna() # 归一化 dc_listings[features] = MinMaxScaler().fit_transform(dc_listings) # 标准化 # dc_listings[features] = StandardScaler().fit_transform(dc_listings) print(dc_listings.shape) dc_listings.head()
输出结果如下:
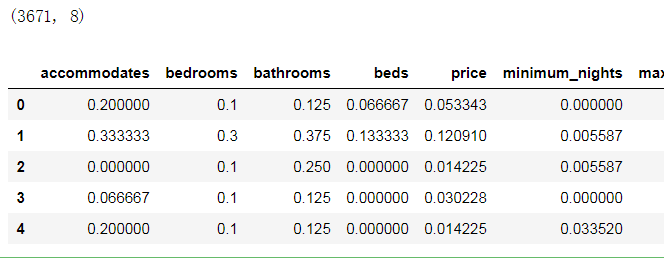
得到标准化的数据后,就可以利用多个指标对房租价格进行预测了。
例如,增加一个Bathrooms指标,对房租价格进行预测。

两个指标计算距离,相当于计算平面上两个点的距离:

也可以利用scipy中的已有工具对距离进行计算。
from scipy.spatial import distance first_listing = dc_listings.iloc[0][['accommodates', 'bathrooms']] second_listing = dc_listings.iloc[20][['accommodates', 'bathrooms']] # 利用euclidean函数计算两个点间的距离 # 点可以是n维,但只能计算两个点的距离 # 结果返回一个数值 distance = distance.euclidean(first_listing, second_listing) distance
结果输出:
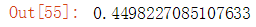
5.多变量的KNN模型
这里选取所有特征进行预测,并对预测结果进行评估。
import pandas as pd from sklearn import preprocessing from sklearn.preprocessing import MinMaxScaler from scipy.spatial import distance # 数据读取 features = ['accommodates','bedrooms','bathrooms','beds','price','minimum_nights','maximum_nights','number_of_reviews'] dc_listings = pd.read_csv(r'D:\codes_jupyter\数据分析_learning\课件\05_K近邻\listings.csv', engine='python') dc_listings = dc_listings[features] # 数据预处理 dc_listings['price'] = dc_listings.price.str.replace(r'\$|,', '').astype(float) # 对price列进行一定的处理,使其变成float型 origin_listings = dc_listings.dropna() # 对缺失值进行处理,删除有缺失值的数据 norm_dc_listings = origin_listings.copy() norm_dc_listings[features] = MinMaxScaler().fit_transform(norm_dc_listings) # 归一化 # 构造训练集和测试集 train_set = norm_dc_listings[:2792] test_set = norm_dc_listings[2792:] # 价格预测函数 def predict_price_multivariate(new_listing_value, features_cols): temp = train_set # distance.cdist是计算两个集合的距离 # [new_listing_value[features]是使其满足array结构 temp['distance'] = distance.cdist(temp[features], [new_listing_value[features_cols]]) # 以distance以索引,从小到大排序 temp = temp.sort_values('distance') # 取价格的前5行 KNN_5 = temp.price.iloc[:5] # 取平均值进行预测 predict_price = KNN_5.mean() return predict_price # 利用测试集进行预测 test_set['predict_price'] = test_set[features].apply(predict_price_multivariate, features_cols=features, axis=1) # 数据结果预处理,化简为标准化数据,因此预测出来的值也是标准化后的值 # 因此,需要将预测值进行反归一化处理,转化为真实值 # 反归一化处理 scaler = MinMaxScaler() norm_price = scaler.fit_transform(origin_listings['price'].values.reshape(-1, 1)) orig_price = scaler.inverse_transform(test_set['predict_price'].values.reshape(-1, 1)) # 对预测结果进行评估 test_set['square_error'] = (orig_price.ravel() - origin_listings['price'][2792:]) ** 2 mse = test_set['square_error'].mean() rmse = mse ** (1/2) print(rmse)
结果输出如下:

6.KNN模型的sklearn实现
import pandas as pd from sklearn import preprocessing from sklearn.preprocessing import MinMaxScaler from sklearn.neighbors import KNeighborsRegressor from sklearn.metrics import mean_squared_error # 数据读取 features = ['accommodates','bedrooms','bathrooms','beds','price','minimum_nights','maximum_nights','number_of_reviews'] dc_listings = pd.read_csv(r'D:\codes_jupyter\数据分析_learning\课件\05_K近邻\listings.csv', engine='python') dc_listings = dc_listings[features] # 数据预处理 dc_listings['price'] = dc_listings.price.str.replace(r'\$|,', '').astype(float) # 对price列进行一定的处理,使其变成float型 origin_listings = dc_listings.dropna() # 对缺失值进行处理,删除有缺失值的数据 norm_dc_listings = origin_listings.copy() norm_dc_listings[features] = MinMaxScaler().fit_transform(norm_dc_listings) # 归一化 # 构造训练集和测试集 train_set = norm_dc_listings[:2792] test_set = norm_dc_listings[2792:] # 实例化一个KNN回归模型并制定K为14 KNN = KNeighborsRegressor(n_neighbors = 14) # 默认的K为15 KNN.fit(train_set[features], train_set['price']) # 预测 prediction = KNN.predict(test_set[features]) # 评估 mean_squared_error(test_set['price'], prediction) ** 0.5
输出结果如下:
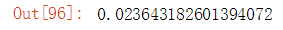
这里利用数据归一化,求出的rmse为上述值。将MinMaxScaler()改为StandardScaler(),利用标准化后的数据求解得到的rmse为: