【学习笔记】浅谈文本生成中的采样方法

    本文学习记录一下，文本生成过程，以及过程中如何 选择/采样 下一个生成的词。首先将简单介绍一下文本生成(text generation)的完成过程；然后简单介绍下常用的采样(sampling)方法；最后，将实现并讨论以下三种采样方法（Greedy Sampling、Temperature Samling、Top-K采样）的优势和劣势。

什么是NLG ?

    语言模型(LM, language model)用于生成文本，一般可分为word-by-word和character-by-character两种级别的方式。
    训练过程中，我们利用一系列token序列(input, X)数据和目标token(targen, y)进行模型训练，期望得到一个能根据输入的序列，生成下一个token的条件概率分布（词汇表长度）的模型。下图案例表示在给定输入为"I want to cook"序列时，word-Level LM预测一个词汇表长度的条件概率分布的过程。

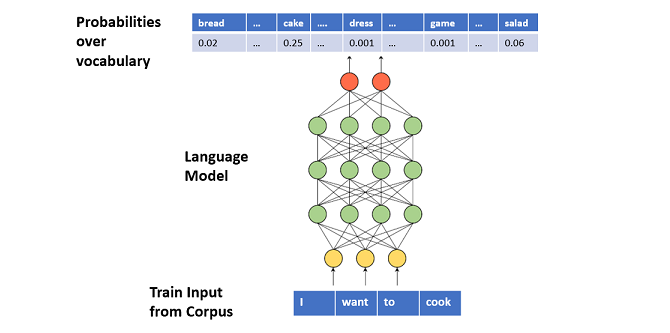
    文本生成过程主要分为一下四个步骤：

• step1: 给定一个句子的序列作为LM的输入
• step2:LM输出一个词汇表长度的概率分布
• step3: 从概率分布中，依据某种策略，sample一个词。
• step4: 将sample到的词，拼接到生成文本的字符串
• step5: 继续输入下一个新序列，重复上述过程。
  

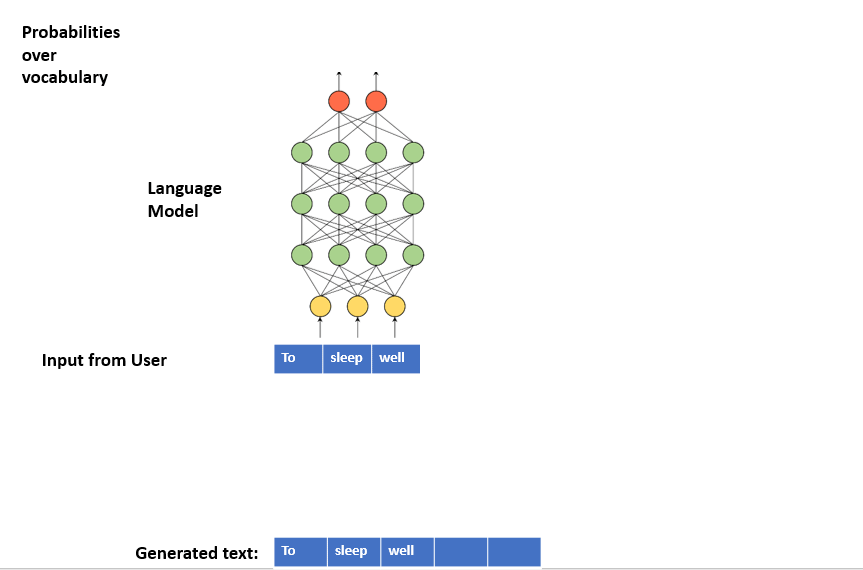
NLG解码策略

    在文本生成任务中，sampling是指按照LM模型生成的所有token的条件概率分布，随机选择一个token。这意味着，在语言模型生成概率分布后，采取哪种策略来选择下一个token,显得极其重要。常见的策略有：

• Greedy Search (Maximization)
• Beam Search
• Temperature Sampling
• Top-K Sampling
• Top-P Sampling (Nucleus sampling)
      本文将着重介绍前面三种方法及其实现，并在后面简单介绍其他两种方法的思想。

1.训练一个语言模型

    本文着重关注的是采样（sampling）的方法及其实现，因此我们假设我们已经有了一个LM，该模型能够根据我们的输出，输出一个词汇表长度的概率分布。具体假设如下：

• 选择文本生成方式为 character-by-character.
• 词汇表（vocabulary）中的字符为'a' to 'z'.
• 已根据一定的预料，训练好语言模型（ Language Model ）
• 该Language Model 能够根据输入序列生成一个词汇表长度的条件概率分布。
• 现在，我们需要的是根据概率分布，sample (select) 下一个 token。

1.1 定义词典

dictionary =[]
for c in range(ord('a'), ord('z')+1):
    dictionary.append(chr(c))

1.2 模拟一个已训练好的LM

class language_model:
    def __init__(self, dictionary):
        self.dictionary = dictionary
    def predict(self):
        output= np.random.rand(len(dictionary))
        output=output/output.sum()
        return  output

# model=language_model(dictionary)

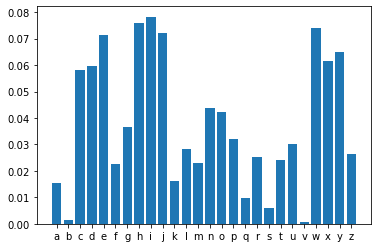
1.3 模拟生成的条件概率分布

predictions= model.predict()
plt.bar(dictionary,predictions)
plt.show()

    经过上述假设，我们可以开始下面的采样策略的实现了。

常见采样策略

Greedy Search解码

    Greedy search方法的思想较为简单，就是直接选择概率分布中概率最大的token（（或字符））作为当前解码出来的词（或字符）。 但是，该方法的问题在于，如果我们总是选择概率最大的词，将会生成很多重复的句子( get stuck in loops )，例如“I don’t know. I don’t know. I don’t know. I don’t know.”样例代码如下：

def greedy_search(conditional_probability):
#     print(np.argmax(conditional_probability))
    return (np.argmax(conditional_probability))

print(predictions)
next_token = greedy_search(predictions)
print(next_token)
print("Sampled token: ",dictionary[next_token])

输出：
[0.01558192 0.00141205 0.05824388 0.05974056 0.07144658 0.02249477
0.03664056 0.07573829 0.0782964 0.07217844 0.01622408 0.02825687
0.02290704 0.04392459 0.04238757 0.03190642 0.00968754 0.02540264
0.00605495 0.02393471 0.03006855 0.00061328 0.07406862 0.06144887
0.06505202 0.02628881]
8
Sampled token: i

Beam Search 解码

    另一种比较流行的解码方法叫beam search，该方法是对greedy search的扩展版本，返回一系列最有可能的输出序列。
    和greedy search选择可能性最大的构成序列不同，beam search在\(t\)步时，生成$t + 1$步的所有可能组成，并从中选择k个概率最大的组合，其中k为指定的搜索参数。
    我们在开始的位置不用随机选择，而是选择K个最可能在开始位置的词语作为序列的第一个词。
    当K取1时，即为Greedy Search，而在大多数机器翻译的任务中 K一般取值5-10。当K较大时，往往会带来较好的结果，因为保留更多的选择性，更可能带来最佳的组合，相应的，也会增加计算成本和解码速度。
    举例说明上述表述。首先，定义一个函数，该函数在给定一个序列（假设长度为N, 词汇表长度为V）的概率分布(矩阵，N x V)，以及搜索参数K时，得到解码结果。在每一个step，每一个候选子序列( candidate sequence)扩展所有可能的下一个子token，然后按照score进行排序，并选择score最大的K个子序列，作为当前step的解码结果。重复上述过程，直到迭代结束。
    一般来说，概率值时较小的数值，经过一些列连乘后，会更小，为防止下溢（underflowing the floating point numbers),将其计算转换为取其对数，然后相加的过程。样例代码如下：

from math import log
from numpy import array
from numpy import argmax

def beam_search_decoder(data, k):
	sequences = [[list(), 0.0]]
	# 迭代序列中的每一步
	for row in data:
		all_candidates = list()
		# 计算每种 hypotheses 的分值，并存储到 all_candidates
		for i in range(len(sequences)):
			seq, score = sequences[i]
			for j in range(len(row)):
				candidate = [seq + [j], score - log(row[j])]
 				# print("da, ", candidate)
				all_candidates.append(candidate)
			print(f"j={j},all_cand={all_candidates}")
		# 对所有的候选序列，通过 score 排序
		ordered = sorted(all_candidates, key=lambda tup:tup[1])
		# 选择 K 个分 score 最高的
		sequences = ordered[:k]
	return sequences

    结果如下：

n = 10

data = []
for i in range(10):
    prediction = model.predict()
    data.append(prediction)

data = array(data)
# print(data)
result = beam_search_decoder(data, 5)

for seq in result:
	print(seq)

---

TEMPERATURE 采样

    Temperature sampling 的想法源于热力统计学的概念，温度高往往意味着更容易是低能量状态。在概率模型中， logits 代表能量值，将其送入softmax函数钱，除以temperature值，得到最终的采样概率分布。 一个Temperature Sampling的keras实现案例。

0. 绘制模型生成的条件概率分布

plt.bar(dictionary,predictions)
plt.show()

1. 使用 “temperature” Reweighting 分布

temperature=0.2
conditional_probability = np.asarray(predictions).astype("float64")
conditional_probability = np.log(conditional_probability) / temperature
plt.bar(dictionary,conditional_probability)
plt.show()

2. 应用 softmax 函数

    softmax函数的原理是将集合中每个元素转化成对应的指数形式，然后分别处理所有元素指数的和，公式如下：

def softmax(z):
    return np.exp(z)/sum(np.exp(z))

reweighted_conditional_probability = softmax(conditional_probability)
plt.bar(dictionary,reweighted_conditional_probability)
plt.show()

3. 从 reweighted 的分布中，重新采样下一个字母

    我们采用多项式分布( **multinomial distribution**)从中sample一个token。多项式分布函数中的 参数有：

• n: int, Number of experiments.

• pvals: sequence of floats, length p. Probabilities of each of the p different outcomes. These must sum to 1 (however, the last element is always assumed to account for the remaining probability, as long as sum(pvals[:-1]) <= 1).

• size: int or tuple of ints, optional. Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn. Default is None, in which case a single value is returned.

    我们调用多项式分布函数，并设置参数为(1, reweighted_conditional_probability, 1) ，因为我们只需要实验一次，并从概率分布中sample出一个结果。 样例代码如下：

probas = np.random.multinomial(1, reweighted_conditional_probability, 1)
plt.bar(dictionary,np.squeeze(probas))
plt.show()

4 把之前的操作放在一起

def temperature_sampling (conditional_probability, temperature=1.0):
    conditional_probability = np.asarray(conditional_probability).astype("float64")
    conditional_probability = np.log(conditional_probability) / temperature
    reweighted_conditional_probability = softmax(conditional_probability)
    probas = np.random.multinomial(1, reweighted_conditional_probability, 1)
    plt.bar(dictionary,reweighted_conditional_probability)
    plt.show()

    return np.argmax(probas)
    
 for temp in np.arange(0.2,1.6,0.8):
    next_token = temperature_sampling(predictions, temperature=temp)
    print("Temperature: ", temp)
    print("Sampled token: ",dictionary[next_token],"\n")

5. 一些观察后的结论

    在大多数研究中, tempreature的选择，往往呈现如下规律：

• 当 temperature 设置为较小或者0的值时， Temperature Sampling 等同于 每次选择最大概率的 Greedy Search。

• 小的temperature 会引发极大的 repetitive 和predictable文本，但是文本内容往往更贴合语料(highly realistic)，基本所有的词都来自与语料库。

• 当temperatures较大时, 生成的文本更具有随机性( random)、趣味性( interesting)，甚至创造性( creative); 甚至有些时候能发现一些新词(misspelled words) 。

• 当 设置高 temperature时，文本局部结构往往会被破坏，大多数词可能会时semi-random strings 的形式。

• 实际应用中，往往experiment with multiple temperature values! 当保持了一定的随机性又能不破坏结构时，往往会得到有意思的生成文本。

Top K 采样

原文链接(Fan et. al, 2018) 该论文介绍了一种新的简单但是高效的采样方法，Top-K sampling。

    在Top-K 采样中, 依旧是从概率分布中，依据概率最大选择k个单词中，不同的点在于，该方法会对这K个词的概率重新再次进行分布(redistributed)，然后依据新的概率分布重新取下一个token。GPT2模型就是用的这种采样方法，使其在故事生成（story generation）方面较为成熟。具体如下

1.首先我们有一个概率分布

predictions= model.predict()
plt.bar(dictionary,predictions)
plt.show()

2.选择top K分布

    我们使用函数tf.math.top_k() 在概率分布中输出 最大的 k 个 实体的值(values)及其对应的索引(indices )。通过索引，我们能得到其对应的tokens.

k=5
top_k_probabilities, top_k_indices= tf.math.top_k(predictions, k=k, sorted=True)
top_k_indices = np.asarray(top_k_indices).astype("int32")
top_k_tokens=[dictionary[i] for i in top_k_indices]
top_k_indices, top_k_tokens
# top_k_probabilities.numpy().sum()

(array([ 8, 7, 22, 9, 4]), ['i', 'h', 'w', 'j', 'e'])

3. 应用softmax函数

top_k_redistributed_probability=softmax(np.log(top_k_probabilities))
top_k_redistributed_probability = np.asarray(top_k_redistributed_probability).astype("float32")
print('top_k_tokens: ',top_k_tokens)
print('top_k_redistributed_probability: ',top_k_redistributed_probability)
print('Total probability: ', top_k_redistributed_probability.sum())

top_k_tokens: ['h', 'p', 'n', 'i', 'k']
top_k_redistributed_probability: [0.21983118 0.21332353 0.21130912 0.19023508 0.16530107]
Total probability: 1.0

plt.bar(top_k_tokens,top_k_redistributed_probability)
plt.show()

4.从 reweighted 的分布中，重新采样下一个字母

sampled_token = np.random.choice(top_k_indices, 
                                 p=top_k_redistributed_probability)
print("Sampled token id: ",sampled_token, 
      " token: ",dictionary[sampled_token])

Sampled token id: 11 token: l

5. 完整过程

  def top_k_sampling(conditional_probability, k):
    top_k_probabilities, top_k_indices= tf.math.top_k(predictions, k=k, sorted=True)
    top_k_indices = np.asarray(top_k_indices).astype("int32")
    top_k_redistributed_probability=softmax(np.log(top_k_probabilities))
    top_k_redistributed_probability = np.asarray(top_k_redistributed_probability).astype("float32")
    sampled_token = np.random.choice(top_k_indices, p=top_k_redistributed_probability)
    top_k_tokens=[dictionary[i] for i in top_k_indices]
    plt.bar(top_k_tokens,top_k_redistributed_probability)
    plt.show()
    return sampled_token

predictions= model.predict()
plt.bar(dictionary,predictions)
plt.show()

6.使用 top-k 采样 different k values

for k in range (5, 25, 5):
  next_token = top_k_sampling(predictions, k=k)
  print("k: ", k)
  print("Sampled token: ",dictionary[next_token],"\n")

7. 一些观察后的结论

    基本top k的采样方法，能够提升生成质量，因为它会把概率较低的结果丢弃（ removing the tail），因此能使得生成过程不那么偏离主题。
    但是一些情况下：

• 丢弃掉的部分（Tail）可能会包含很多的词语，这导致我们能选择的词汇较少。

• 而在一些情况下，丢弃掉大部分可能包含的词汇较少，我们能生成较为丰富的文本。

    因此， k 值的选择对于生成结果极其重要。

Top p采样

    有很多采样的方法被提出来，top p也是其中一种最为常见的方法。

• Top-P Sampling (Nucleus sampling): 与top k对低概率词汇直接丢弃的处理方法不同，top p采用的是累计概率的方式。即从累计概率超过某一个阈值p的词汇中进行采样。换言之，根据参数p的大小调节(0<=p<=1), Top-P Sampling增大了出现概率较小的词汇的生成的概率。 更多细节说明样例代码：

def scatter_values_on_batch_indices(values, batch_indices):
    shape = shape_list(batch_indices)
    # broadcast batch dim to shape
    broad_casted_batch_dims = tf.reshape(tf.broadcast_to(tf.expand_dims(tf.range(shape[0]), axis=-1), shape), [1, -1])
    # transform batch_indices to pair_indices
    pair_indices = tf.transpose(tf.concat([broad_casted_batch_dims, tf.reshape(batch_indices, [1, -1])], 0))
    # scatter values to pair indices
    return tf.scatter_nd(pair_indices, tf.reshape(values, [-1]), shape)


def set_tensor_by_indices_to_value(tensor, indices, value):
    # create value_tensor since tensor value assignment is not possible in TF
    value_tensor = tf.zeros_like(tensor) + value
    return tf.where(indices, value_tensor, tensor)


def shape_list(x):
    """Deal with dynamic shape in tensorflow cleanly."""
    static = x.shape.as_list()
    dynamic = tf.shape(x)
    return [dynamic[i] if s is None else s for i, s in enumerate(static)]

def top_p_decoding(logits, top_p=1.0, filter_value=-float("Inf"), min_tokens_to_keep=1):
    sorted_indices = tf.argsort(logits, direction="DESCENDING")
    sorted_logits = tf.gather(
        logits, sorted_indices, axis=-1, batch_dims=1
    )  # expects logits to be of dim (batch_size, vocab_size)

    cumulative_probs = tf.math.cumsum(tf.nn.softmax(sorted_logits, axis=-1), axis=-1)

    # Remove tokens with cumulative probability above the threshold (token with 0 are kept)
    sorted_indices_to_remove = cumulative_probs > top_p

    if min_tokens_to_keep > 1:
        # Keep at least min_tokens_to_keep (set to min_tokens_to_keep-1 because we add the first one below)
        sorted_indices_to_remove = tf.concat(
            [
                tf.zeros_like(sorted_indices_to_remove[:, :min_tokens_to_keep]),
                sorted_indices_to_remove[:, min_tokens_to_keep:],
            ],
            -1,
        )

    # Shift the indices to the right to keep also the first token above the threshold
    sorted_indices_to_remove = tf.roll(sorted_indices_to_remove, 1, axis=-1)
    sorted_indices_to_remove = tf.concat(
        [tf.zeros_like(sorted_indices_to_remove[:, :1]), sorted_indices_to_remove[:, 1:]],
        -1,
    )
    # scatter sorted tensors to original indexing
    indices_to_remove = scatter_values_on_batch_indices(sorted_indices_to_remove, sorted_indices)
    logits = set_tensor_by_indices_to_value(logits, indices_to_remove, filter_value)
    return logits

---

n = 10

data = []
for i in range(10):
    prediction = model.predict()
    data.append(prediction)
data = array(data)
print(data)
result = top_p_decoding(data, 0.5)

for seq in result:
	print(seq)

---

总结

    本文讨论了文本生成过程中的一些常见的采样方法及其部分实现。也讨论了不同方法间的优缺点。总体而言，没有最好的方法，只有最适合任务的方法，推荐结合具体任务通过反复实验找到最佳的生成方法。推荐使用不同的参数，在生成文本的结构性和随机性之间进行权衡，来得到有意思的文本生成结果。