【学习笔记:】3-线性回归与逻辑回归

1. 背景

    学习某培训平台核心基础课程第三课（第二课内容后续补上）内容，特此笔记，供加深印象。
    本将内容主要有两个模型：线性回归和逻辑归回；应用在波斯顿房价预测的数据集上(sklearn.datasets的load_boston)。首先任务热力图(heatmap)分析各个特征间的相关系数(dataframe.corr()),选择了两个对房价（target）影响最大的特征RM和LSTAT；然后分别构建线性模型（Linear regression）对房价进行预测拟合、利用逻辑回归模型判断某个房子是否属于高档小区。

2. 案例

2.1 Linear Regression

    以某数据集为例，通过热力图分析各个特征之间的相关系数，选择对预测值（price）影响最大的两个特征，用来模拟价格。
    主要业务包括：1.构造数据集。2.特征分析。分析各个特征间的相关系数，并用热力图展示。 3.构造模型。4. 构造损失函数。5.梯度更新。 6.可视化展示。
业务分析：

• 以伦敦房价数据集为例子（from sklearn.datasets import loda_boston）
• 通过各特征相关系数(corr)的heatmap图分析，选择两个对房价影响最大的特征，作为\(x_1,x_2\)
• 用线性模型，模拟\(x_1,x_2\)与房价（target）的线性关系，即：寻找\(w_1,w_2,b\) 使得：\(w_1 * x_1 + w_2 * x_2 + b\) 的值（\(\hat{y}\)）与price（\(y\)）相差(\(损失,loss\))越小越好。
• 损失函数，选择均方损失\(\sum(\hat{y} - y)^2\)越小越好。其中，\(\hat{y} = w_1 * x_1 + w_2 * x_2 + b\)
• 对\(w_1 w_2\) 进行梯度更新（求偏导） \(\frac{1}{N}\sum x_1 * (\hat{y} - y) * 2\); \(\frac{1}{N}\sum x_2 * (\hat{y} - y) * 2\).
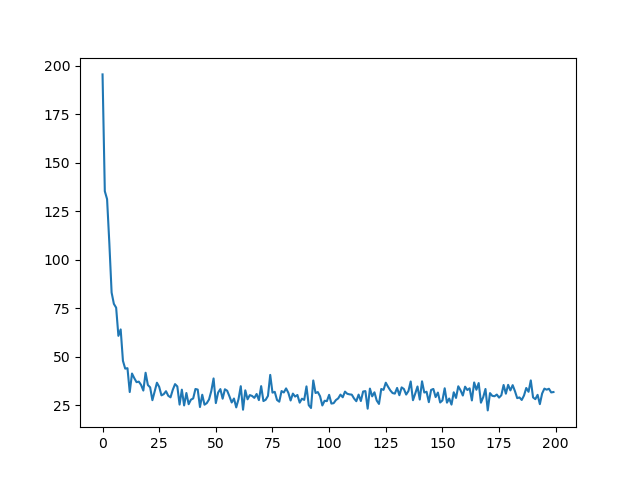
• 损失下降的图

# 构造数据集
def get_dataset():
    dataset = load_boston()

    data = dataset['data']
    target = dataset['target']

    dataframe = pd.DataFrame(data)
    dataframe.columns = dataset['feature_names']
    dataframe['price'] = target  # 添加target列到特征，分析price/target与各特征的相关系数

    # # 特征相关系数分析
    # sns.heatmap(dataframe.corr(), annot=True, fmt='.1f')
    # plt.show()
    """
    选择特征RM(小区平均卧室个数) 和 LSTAT（低收入人群在周围的比例）两个特征
    """
    rm, lstat = dataframe['RM'], dataframe['LSTAT']
    return rm, lstat, target

# 定义模型
def model(x, w, b):
    return np.dot(x, w.T) + b

# 定义损失
def loss(yhat, y):
    return np.mean((yhat - y) ** 2)

# 定义偏导
def partial_w(x, y, yhat):
    return np.array([ np.mean(2 * (yhat - y) * x[0]), np.mean(2 * (yhat - y) * x[1]) ])
	
def partial_b(x, y, yhat):
    return np.mean(2 * (yhat - y))

效果图如下：

完整代码如下：

# coding=utf-8
from sklearn.datasets import load_boston
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import random
import numpy as np
""""
业务分析：
    1. 以伦敦房价数据集为例子（from sklearn.datasets import loda_boston）
    2. 通过各特征相关系数(corr)的heatmap图分析，选择两个对房价影响最大的特征，作为x1, x2
    3. 用线性模型，模拟x1, x2与房价（target）的线性关系，即：寻找w1, w2, b使得：
        w1 * x1 + w2 * x2 + b 的值（yhat）与price（target）相差(损失)越小越好
    4. 损失函数，选择均方损失 sum (yhat - y)^2 越小越好，yhat = w1 * x1 + w2 * x2 + b
    5. 对w1 w2 进行梯度更新（求偏导） sum x1 * (yhat - y) * 2; sum x2 * (yhat - y)  * 2;
    6. 损失下降的图
"""

def get_dataset():

    dataset = load_boston()

    data = dataset['data']
    target = dataset['target']

    dataframe = pd.DataFrame(data)
    dataframe.columns = dataset['feature_names']
    dataframe['price'] = target  # 添加target列到特征，分析price/target与各特征的相关系数

    # # 特征相关系数分析
    # sns.heatmap(dataframe.corr(), annot=True, fmt='.1f')
    # plt.show()
    """
    选择特征RM(小区平均卧室个数) 和 LSTAT（低收入人群在周围的比例）两个特征
    """
    rm, lstat = dataframe['RM'], dataframe['LSTAT']
    return rm, lstat, target

def partial_b(x, y, yhat):
    return np.mean((yhat - y) * 2)

def partial_w(x, y, yhat):
    return np.array([2 * np.mean((yhat - y) * x[0]), 2 * np.mean((yhat - y) * x[1])])

def loss(yhat, y):
    return np.mean( (yhat - y) ** 2 )

def model(x, w, b):
    return np.dot(x, w.T) + b

def train(x1, x2, target):

    # 超参数
    epochs = 200
    learning_rate = 1e-5

    # 初始化
    w = np.random.random_sample((1, 2))
    b = 0

    loss_total = []
    for epoch in range(epochs):

        loss_batch = []
        # batch training
        for batch in range(len(x1)):
            index = random.choice(range(len(x1)))

            x = np.array([x1[index], x2[index]])
            y = np.array(target[index])

            # 模型预测值
            yhat = model(x, w, b)

            # 损失值
            loss_ = loss(yhat, y)
            loss_batch.append(loss_)
            if batch % 100 == 0:
                print(f'Epoch: {epoch}, Batch: {batch}, Loss: {loss_}')

            # 参数更新
            w = w + -1 * partial_w(x, y, yhat) * learning_rate
            b = b + -1 * partial_b(x, y, yhat) * learning_rate

        loss_total.append(np.mean(np.array(loss_batch)))

    # 可视化
    sns.lineplot(x=range(len(loss_total)), y=loss_total)
    plt.show()


def main():

    # 1. 构造数据集合
    x1, x2, target = get_dataset()

    # 模型训练
    train(x1, x2, target)

    # 模型评估

    # 模型预测

if __name__ == '__main__':
    main()

2.2 Logistic Regression

    逻辑回归部分任然采用的是该数据集，但是用来预测某个房子是否为高档小区，因此逻辑回归模型，实际是一个分类模型，用于处理分类任务。
    基本流程和2.1相同。逻辑回归模型的核心是将预测值\(\hat{y}\)结合sigmoid函数，转化为概率的形式(0-1之间）。

# 构造数据（标签）

# 用百分位数分析价格(第66百分位数的值为多少)
greater_than_most = np.percentile(dataframe['price'], 66)

# 设置价格超过百分值66的房子，为高档小区
dataframe['expensive'] = dataframe['price'].apply(lambda p: int(p > greater_than_most))

# 定义model 和sigmoid

def sigmoid(x):
    return 1 / (np.exp(-x) + 1)

def model(x, w, b):
    return sigmoid(np.dot(x, w.T) + b)

    对比线性回归部分，可知逻辑回归只是再把预测值，送入到sigmiod函数中，
而该函数将数值转化0-1之间。

# 定义损失函数和偏导
def loss(yhat, y):
    return -1 * np.sum(y * np.log(yhat) + (1 - y) * np.log(1 - yhat))

def partial_w(x, y, yhat):
    return np.array([np.sum(2 * (y - yhat) * x[0]), np.sum(2 * (yhat - y) * x[1])])

def partial_b(x, y, yhat):
    return np.sum((y - yhat) * 2)

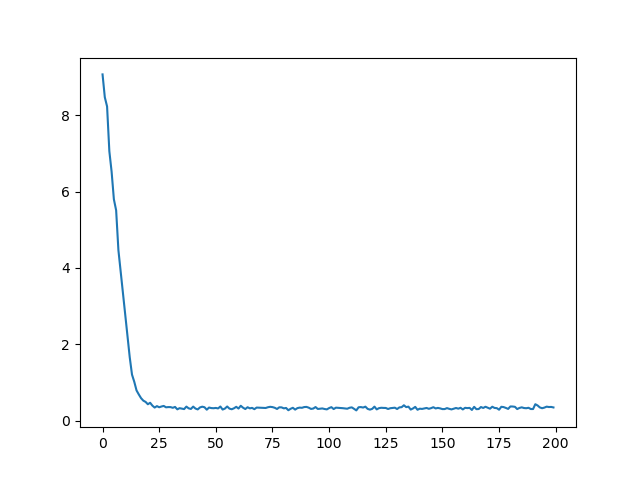
效果图如下：

完整代码如下：

# coding=utf-8
from sklearn.datasets import load_boston
import seaborn as sns
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import random

"""
业务背景：
    1. 用伦敦房价做分类任务，判断小区是否为高档小区（0-1分类）
    2. 选择两个特征，利用sigmoid函数作为转换
"""

def get_dataset():
    dataset = load_boston()

    data = dataset['data']
    target = dataset['target']

    dataframe = pd.DataFrame(data)
    dataframe.columns = dataset['feature_names']
    dataframe['price'] = target

    # 用百分位数分析价格(第66百分位数的值为多少)
    greater_than_most = np.percentile(dataframe['price'], 66)
    # 设置价格超过百分值66的房子，为高档小区
    dataframe['expensive'] = dataframe['price'].apply(lambda p: int(p > greater_than_most))

    # 添加一列，高档小区

    return dataframe['RM'], dataframe['LSTAT'], dataframe['expensive']

def sigmoid(x):
    return 1 / (np.exp(-x) + 1)

def model(x, w, b):

    return sigmoid(np.dot(x, w.T) + b)

def partial_w(x, y, yhat):
    return np.array([np.sum((yhat -y) * x[0]), np.sum((yhat -y) * x[1])])

def partial_b(x,y, yhat):
    return np.sum(yhat - y)

def loss(yhat, y):
    """
    -1 * sum [ y*log (yhat) + (1-y)*log(1-hat)]
    :param yhat:
    :param y:
    :return:
    """
    return -1 * np.sum(y * np.log(yhat) + (1 - y) * np.log(1 - yhat))

def train(rm, lstat, label):

    # 超参数
    epochs = 200
    learning_rate = 1e-5

    # 初始化
    w = np.random.random_sample((1, 2))
    b = 0

    loss_total = []
    for epoch in range(epochs):

        loss_batch = []
        for batch in range(len(rm)):

            # 每次只用一个数据
            index = random.choice(range(len(rm)))

            x = np.array([rm[index], lstat[index]])
            y = label[index]

            yhat = model(x, w, b)

            loss_ = loss(yhat, y)
            loss_batch.append(loss_)
            if batch % 100 == 0:
                print(f'Epoch: {epoch}, Batch: {batch}, Loss: {loss_}')

            w = w + -1 * partial_w(x, y, yhat) * learning_rate
            b = b + -1 * partial_b(x, y, yhat) * learning_rate

        loss_total.append(np.mean(np.array(loss_batch)))

    sns.lineplot(x=range(len(loss_total)), y=loss_total)
    plt.show()


def main():

    # 1. 构造数据集
    rm, lstat, label = get_dataset()

    # 2. 模型训练
    train(rm, lstat, label)


if __name__ == '__main__':
    main()

3. 总结

• 逻辑回归虽然也叫回归，但实际上是一个分类器，用于分类任务中。
• 后续更新

4. 其他

• 后续继续完善