排序算法总结----运算类排序
运算排序
第一：计数排序
1：原理
对于每个输入数，确定小于该数的个数。这样可以直接把数放在输出数组的位置。
2：性能
最差时间复杂度
最优时间复杂度
平均时间复杂度
最差空间复杂度
注：稳定算法
3：应用
适合0~100的范围的数，当然可以和基排序结合而扩展数的范围。
4：实现
void CountingSort(int *A, int *B, int array_size, int k) { int i, value, pos; int * C=new int[k+1]; for(i=0; i<=k; i++) { C[i] = 0; } for(i=0; i< array_size; i++) { C[A[i]] ++; } for(i=1; i<=k; i++) { C[i] = C[i] + C[i-1]; } for(i=array_size-1; i>=0; i--) { value = A[i]; pos = C[value]; B[pos-1] = value; C[value]--; } delete [] C; }
第二：基排序
1：原理
它是一种扩数的排序，将数值大的分解成小值排序；蕴含一种分配收集思想，从个位数开始不断分配收集，直到最高位为止。注意其中分配集中排序是一个稳定的排序，这是个要求。
2：性能
最差时间复杂度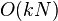
k表示位数，N表示稳定算法的时间
最差空间复杂度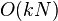k表示位数，N表示稳定算法损耗空间
注意：算法稳定
3：应用
显然是所有位数相同，位数不大时应用是很合适的。
4：实现---方式有从高位，也有从低位开始的
1)低位开始+计数稳定排序
int GetDigit(int x,int d) { int a[] = {1, 1, 10, 100}; //最大三位数，所以这里只要百位就满足了。 return (x/a[d]) % 10; } void LsdradixSort(int* arr,int begin,int end,int d) { const int radix = 10; int count[radix], i, j; int *bucket =new int[end-begin+1]; //所有桶的空间开辟 //按照分配标准依次进行排序过程 for(int k = 1; k <= d; ++k) { //置空 for(i = 0; i < radix; i++) { count[i] = 0; } //统计各个桶中所盛数据个数 for(i = begin; i <= end; i++) { count[GetDigit(arr[i], k)]++; } //count[i]表示第i个桶的右边界索引 for(i = 1; i < radix; i++) { count[i] = count[i] + count[i-1]; } //把数据依次装入桶(注意装入时候的分配技巧) for(i = end;i >= begin; --i) //这里要从右向左扫描，保证排序稳定性 { j = GetDigit(arr[i], k); //求出关键码的第k位的数字， 例如：576的第3位是5 bucket[count[j]-1] = arr[i]; //放入对应的桶中，count[j]-1是第j个桶的右边界索引 --count[j]; //对应桶的装入数据索引减一 } //注意：此时count[i]为第i个桶左边界 //从各个桶中收集数据 for(i = begin,j = 0; i <= end; ++i, ++j) { arr[i] = bucket[j]; } } delete [] bucket; }
2)高位开始
int GetDigit(int x,int d) { int a[] = {1, 1, 10, 100}; //最大三位数，所以这里只要百位就满足了。 return (x/a[d]) % 10; } void MsdradixSort(int arr[],int begin,int end,int d) { const int radix = 10; int count[radix], i, j; //置空 for(i = 0; i < radix; ++i) { count[i] = 0; } //分配桶存储空间 int *bucket = new int [end-begin+1]; //统计各桶需要装的元素的个数 for(i = begin;i <= end; ++i) { count[GetDigit(arr[i], d)]++; } //求出桶的边界索引，count[i]值为第i个桶的右边界索引+1 for(i = 1; i < radix; ++i) { count[i] = count[i] + count[i-1]; } //这里要从右向左扫描，保证排序稳定性 for(i = end;i >= begin; --i) { j = GetDigit(arr[i], d); //求出关键码的第d位的数字， 例如：576的第3位是5 bucket[count[j]-1] = arr[i]; //放入对应的桶中，count[j]-1是第j个桶的右边界索引 --count[j]; //第j个桶放下一个元素的位置(右边界索引+1) } //注意：此时count[i]为第i个桶左边界 //从各个桶中收集数据 for(i = begin, j = 0;i <= end; ++i, ++j) { arr[i] = bucket[j]; } //释放存储空间 delete []bucket; //对各桶中数据进行再排序 for(i = 0;i < radix; i++) { int p1 = begin + count[i]; //第i个桶的左边界 int p2 = begin + count[i+1]-1; //第i个桶的右边界 if(p1 < p2 && d > 1) { MsdradixSort(arr, p1, p2, d-1); //对第i个桶递归调用，进行基数排序，数位降 1 } } }
注：显然从低位开始要好，因为没有递归。
第三：桶排序
1：原理
利用函数映射将其映射到有限的点上，也就是所谓的桶，使得每个桶有个比较均匀的个数；使得输出时，就是已经根据桶编号将组间数排序完毕，剩下的就是拍桶内的数值了。
2：性能
最差时间复杂度
平均时间复杂度
最差空间复杂度
3：应用
一般是配合其他算法一起应用，桶外使用这种规则，桶内需要使用桶内排序；这里有桶的规划，使得桶内数据个数均匀，这样的桶是比较合适，桶内数据可以用链表存储，也可以用指针指向某个数组。时间上是最快的，空间上损耗最大。
4：实现---不考虑会到同一个桶的情况，也不对桶内处理，直接分到桶，由桶直接输出。
/// <summary> /// 桶排序 /// 1),已知其区间,例如[1..10],学生的分数[0...100]等 /// 2),如果有重复的数字,则需要 List<int>数组,这里举的例子没有重复的数字 /// </summary> /// <param name="unsorted">待排数组</param> /// <param name="maxNumber">待排数组中的最大数,如果可以提供的话</param> /// <returns></returns> static int[] bucket_sort(int[] unsorted, int maxNumber = 99) { int[] sorted = new int[maxNumber + 1]; for (int i = 0; i < unsorted.Length; i++) { sorted[unsorted[i]] = unsorted[i]; } return sorted; }
第四：鸽巢排序
1：原理
和桶一样，只是对相同数，进行了处理
2：性能
时间：
空间：
3：应用
适合相同数多，数的范围不大，有点像基排序。
4：实现
/// 鸽巢排序 /// </summary> /// <param name="unsorted">待排数组</param> /// <param name="maxNumber">待排数组中的最大数,如果可以指定的话</param> /// <returns></returns> static int[] pogeon_sort(int[] unsorted, int maxNumber = 10) { int[] pogeonHole = new int[maxNumber + 1]; foreach (var item in unsorted) { pogeonHole[item]++; } return pogeonHole; /* * pogeonHole[10] = 4; 的含意是 * 在待排数组中有4个10出现,同理其它 */ }--->打印时，只需要对非0处的，打印，还会是稳定打印。
第五：耐心排序
1：原理
这个排序的关键在建桶和入桶规则上
建桶规则:如果没有桶,新建一个桶;如果不符合入桶规则那么新建一个桶
入桶规则:只要比桶里最上边的数字小即可入桶,如果有多个桶可入,那么按照从左到右的顺序入桶即可
分完桶后，也就是分完组后，就进行插入排序。。。。。
桶的结构使用栈要好些，就是看栈顶；
2：性能
显然这种复杂度和插入排序差不多，这个只是让原来的数据有一定规律而已。。。
3：应用
应用不多
4：实现
省略、、、、、、
第六：珠排序
1：原理
数的分解后，自由落体。
精华如下图
2：性能
3：应用
显然适用性不够
4：实现
待定。。。。。
第七：ProxmapSort
1：原理
就是桶算法---里有桶内排序，只是桶内排序适用基排序
2：性能
3：应用
4：实现
第八：FlashSort
1：原理
FlashSort依然类似桶排,主要改进了对要使用的桶的预测,或者说,减少了无用桶的数量从而节省了空间,例如
待排数字[ 6 2 4 1 5 9 100 ]桶排需要100个桶,而flash sort则由于可以预测桶则只需要7个桶。
预测桶号细节
待排数组[ 6 2 4 1 5 9 ]
具体看6可能出现的桶号
Ai - Amin 是 6 - 1 = 5
Amax - Amin 是9 - 1 = 8
m - 1 是数组长度6 - 1 = 5
则(m - 1) * (Ai - Amin) / (Amax - Amin) = 5 * 5 / 8 =25/8 = 3.125
最后加上1等于 4.125
6预测的桶号为4.125
2预测的桶号为1.625
4预测的桶号为2.875
1预测的桶号为1
5预测的桶号为3.5
9预测的桶号为5
去掉小数位后,每个数字都拥有自己预测的桶号,对应如下所示
待排数组[ 6 2 4 1 5 9 ]
预测桶号[ 4 1 2 1 3 5 ]
入桶规则
1号桶 2,1
2号桶 4
3号桶 5
4号桶 6
5号桶 9
1号桶内两个数字使用任意排序算法使之有序,其它桶如果此种情况同样需要在桶内排序,使用什么排序算法不重要,重要的是排成从小到大即可
最后顺序从桶里取出来即可
[1 2 4 5 6 9]
2：性能
3：应用
4：实现
第九：经典排序算法 - Strand Sort
Strand sort是思路是这样的,它首先需要一个空的数组用来存放最终的输出结果,给它取个名字叫"有序数组"
然后每次遍历待排数组,得到一个"子有序数组",然后将"子有序数组"与"有序数组"合并排序
重复上述操作直到待排数组为空结束
看例子吧
待排数组[ 6 2 4 1 5 9 ]
第一趟遍历得到"子有序数组"[ 6 9],并将其归并排序到有序数组里
待排数组[ 2 4 1 5]
有序数组[ 6 9 ]
第二趟遍历再次得到"子有序数组"[2 4 5],将其归并排序到有序数组里
待排数组[ 1 ]
有序数组[ 2 4 5 6 9 ]
第三趟遍历再次得到"子有序数组"[ 1 ],将其归并排序到有序数组里
待排数组[ ... ]
有序数组[ 1 2 4 5 6 9 ]
待排数组为空,排序结束
第十：圈排序Cycle Sort
所谓的圈的定义,我只能想到用例子来说明,实在不好描述
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
第一部分
第一步,我们现在来观察待排数组和排完后的结果,以及待排数组的索引,可以发现
排完序后的6应该出现在索引4的位置上,而它现在却在位置0上,
记住这个位置啊,一直找到某个数应该待在位置0上我们的任务就完成了
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
第二步,而待排数组索引4位置上的5应该出现在索引3的位置上
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
第三步,同样的,待排数组索引3的位置是1,1应该出现在位置0上,注意注意,找到这么一个数了:1,它应该待在位置0上
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
第四步,而索引0处却放着6,而6应该出现在索引4的位置,至此可以发现,回到原点了,问题回到第一步了,
所以这里并不存在所谓的第四步,前三步就已经转完一圈了
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
这就是所谓的一圈!真不好描述,不知道您看明白没...汗.
前三步转完一圈,得到的数据分别是[ 6 5 1 ]
第二部分
第一步,圈排序并不是一圈排序,而一圈或多圈排序,所以,还得继续找,这一步从第二个数字2处开始转圈
待排中的2位于索引1处,排序完毕仍然处于位置1位置,所以这一圈完毕,得到圈数据[ 2 ]
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
第三部分
第一步,同上,4也出现了它应该待的位置,结束这一圈,得到第三个圈:[ 4 ]
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
第四部分
第一步,由于1和5出现在第一圈里,这是什么意思呢,说明这两个数已经有自己的圈子了,不用再找了,
即是找,最后还是得到第一圈的数据[ 6 5 1 ],所以,1和5跳过,这一部分实际应该找的是9,来看看9的圈子
9应该出现在索引5的位置,实际上它就在索引5的位置,与第二部分的第一步的情况一样,所以这一圈的数据也出来了:[ 9 ]
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
一共找到四个圈子,分别是
[ 6 5 1 ] , [ 2 ] ,[ 4 ] , [ 9 ]
如果一个圈只有一个数字,那么它是不需要转圈的,即不需要排序,那么只有第一个圈排序即可
你可能要问了,前边的那些圈子都是基于已知排序结果才能得到,我都已知结果还排个毛啊
以上内容都是为了说明什么是圈,知道什么是圈后才能很好的理解圈排序
现在来分解排序的细节
第一步,将6取出来,计算出有4个数字比6小,将6放入索引4,同时原索引4位置的数字5出列
排序之前[ 0 2 4 1 5 9 ] 6
排序之后[ 0 2 4 1 6 9 ] 5
索引位置[ 0 1 2 3 4 5 ]
第二步,当前数字5,计算出有3个数字比5小,将5放入索引3,同时原索引3位置的数字
排序之前[ 0 2 4 1 6 9 ] 5
排序之后[ 0 2 4 5 6 9 ] 1
索引位置[ 0 1 2 3 4 5 ]
第三步,当前数字1,计算出有0个数字比1小,将1放入索引0,索引0处为空,这圈完毕
排序之前[ 0 2 4 5 6 9 ] 1
排序之后[ 1 2 4 5 6 9 ]
索引位置[ 0 1 2 3 4 5 ]
第一个圈[ 6 5 1 ]完毕
第四步,取出下一个数字2,计算出有1个数字比2小,将2放入索引1处,发现它本来就在索引1处
第五步,取出下一个数字4,计算出有2个数字比4小,将4放入索引2处,发现它本来就在索引2处
第六步,取出下一个数字5,5在第一个圈内,不必排序
第七步,取出下一个数字6,6在第一个圈内,不必排序
第八步,取出下一个数字9,计算出有5个数字比9小,将9放入索引5处,发现它本来就在索引5处
全部排序完毕
第十一：图书馆排序(Library Sort)
思路简介,大概意思是说,排列图书时,如果在每本书之间留一定的空隙,那么在进行插入时就有可能会少移动一些书,说白了就是在插入排序的基础上,给书与书之间留一定的空隙,这个空隙越大,需要移动的书就越少,这是它的思路,用空间换时间
进行空间分配的过程
这个我实在是找不到相关的资料,没准就是平均分配嘞
进行插入排序的过程
举例待排数组[ 0 0 6 0 0 2 0 0 4 0 0 1 0 0 5 0 0 9 ],直接对它进行插入排序
第一次移动,直接把2放6前边
[ 0 2 6 0 0 0 0 0 4 0 0 1 0 0 5 0 0 9 ]
第二次移动,先把6往后挪,然后把4放在刚才6的位置,移动了一个位置
[ 0 2 4 6 0 0 0 0 0 0 0 1 0 0 5 0 0 9 ]
第三次移动,直接把1放2前边
[ 1 2 4 6 0 0 0 0 0 0 0 0 0 0 5 0 0 9 ]
第四次移动,再把6往后挪一位,把5放在刚才6的位置
[ 1 2 4 5 6 0 0 0 0 0 0 0 0 0 0 0 0 9 ]
第五次移动后,把9放6后边,排序结束
[ 1 2 4 5 6 9 0 0 0 0 0 0 0 0 0 0 0 0 ]
以上算法排序中，多处不是原创，仅仅是提供给个人做学习笔记适使用。
