5.【。】
题解
T1(一心净土)


(原)
\(10pts\)
- 一开始做一点思路也没有,考完之后一想,最大显然与最小的区间有关,不可能有数大于这个区间,又想到可以循环一个串,就能保证在不小于最小区间的区间里包含所有自然数。
一想真是太 \(\text{SB}\) 了。只拿了部分分,还是只有 \(m=1\) 的分。
代码
#include<bits/stdc++.h>
#define N (50010)
#define int long long
#define sort stable_sort
using namespace std;
namespace IO
{
#define ll long long
const int MAX=1<<25;
char buf[MAX],*p1=buf,*p2=buf;
char obuf[MAX],*o=obuf;
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
//template<typename T>
//inline T read()
inline int read()
{
int x=0;bool f=1;
char c=gc();
for(;c<48||c>57;c=gc())if(c=='-')f=0;
for(;c>=48&&c<=57;c=gc())x=(x<<3)+(x<<1)+(c^48);
return f?x:~x+1;
}
void print(ll x){if(x>9)print(x/10);*o++=(x%10)+'0';}
void pit(ll x){if(x<0)*o++='-',x=~x+1;print(x);}
void write(ll x,char end){pit(x);*o++=end;}
void flush(){fwrite(obuf,o-obuf,1,stdout);}
#undef ll
}
using IO::read;using IO::write;using IO::flush;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x<y?x:y;}
inline void swap(int &x,int &y){int tmp=x;x=y;y=tmp;}
int n,m;
namespace hs
{
int hs[100010],to[100010],nxt[100010];
int mod=98317,head[100010],cnmhs;
void clean(){memset(head,0,sizeof(head));}
void add(int x,int P=mod)
{
hs[++cnmhs]=x,to[cnmhs]=P,x%=mod,
nxt[cnmhs]=head[x],head[x]=cnmhs;
}
int find_x(int x)
{
for(int i(head[x%mod]);i;i=nxt[i])
if(hs[i]==x)return to[i];
return -1;
}
}
namespace math
{
int t,P,q,d;
int x,y,k,ans,possible,lon;
int mod[N],a[N],gt[N],nth_mod[N];
int len,prime[700010],phi[N];//线性筛欧拉函数
short mu[N];
int mtot;
bitset<N>vis;
int jc[N];
long long inv[N];//乘法逆元
long long qpow(long long x,int b,int P=P)
{
long long ans=1;
for(;b;b>>=1){if(b&1)ans=(ans*x)%P;x=(x*x)%P;}
return ans;
}//O(log(b))
int gcd(int a,int b){return b?gcd(b,a%b):a;}
int exgcd(int a,int b,int &x,int &y)
{
if(!b){x=1,y=0;return a;}
int d=exgcd(b,a%b,y,x);
y-=(a/b*x);
return d;
}//O(max(a,b))
int ola(int n)
{
int ans=n;
for(int i=2;i*i<=n;++i)
{
if(n%i==0)ans=ans/i*(i-1);
for(;n%i==0;n/=i);
}
if(n>1)ans=ans/n*(n-1);
return ans;
}//O(sqrt(n))
void eular(int n)//欧拉筛
{
//memset(vis,0,sizeof(vis));
phi[1]=1;
for(int i(2);i<=n;++i)
{
if(!vis[i])
prime[++len]=i,phi[i]=(i-1);
for(int j(1);j<=len&&i*prime[j]<=n;++j)
{
vis[i*prime[j]]=1;
if(!(i%prime[j]))
{phi[i*prime[j]]=(phi[i]*prime[j]);break;}
else phi[i*prime[j]]=(phi[i]*(prime[j]-1));
}
}
}//O(n)
void mobius(int n)
{
//memset(vis,0,sizeof(vis));
mu[1]=1;
for(int i(2);i<=n;++i)
{
if(!vis[i])prime[++mtot]=i,mu[i]=-1;
for(int j(1);j<=mtot&&i*prime[j]<=n;++j)
{
vis[i*prime[j]]=1;
if(!(i%prime[j])){mu[i*prime[j]]=0;break;}
mu[i*prime[j]]=~mu[i]+1;
}
}
}//O(n)
void eular_mobius(int n)
{
//memset(vis,0,sizeof(vis));
mu[1]=phi[1]=1;
for(int i(2);i<=n;++i)
{
if(!vis[i])prime[++len]=i,phi[i]=(i-1),mu[i]=-1;
for(int j(1);j<=len&&i*prime[j]<=n;++j)
{
vis[i*prime[j]]=1;
if(!(i%prime[j]))
{
phi[i*prime[j]]=(phi[i]*prime[j]);
mu[i*prime[j]]=0;
break;
}
phi[i*prime[j]]=(phi[i]*(prime[j]-1));
mu[i*prime[j]]=~mu[i]+1;
}
}
}
void niyuan1(int n,int P=P)//乘法逆元
{
inv[1]=1;
for(int i(2);i<=n;++i)inv[i]=((P-P/i)*inv[P%i])%P;
}//O(n)
int inv_it(int a,int P=P)//O(log(a))
{
int d(exgcd(a,P,x,y));
return(x%P+P)%P;
}
int C(int n,int m,int P=P)
{
if(m>n)return 0;
int a(1),b(1);
for(int i(n-m+1);i<=n;++i)a=(a*i)%P;
for(int i(2);i<=m;++i)b=(b*i)%P;
return(a*qpow(b,P-2,P))%P;
}
int lucas(int n,int m,int P=P)
{return(!m)?1:(C(n%P,m%P,P)*lucas(n/P,m/P,P))%P;}
int excrt(int n)//扩展中国剩余定理
{
int mul(mod[1]);ans=a[1];
int x,y,c,d;
for(int i(2);i<=n;++i)
{
x=y=0;
c=(a[i]-ans%mod[i]+mod[i])%mod[i];
d=exgcd(mul,mod[i],x,y);
if(!(c%d))
ans+=(((x+mod[i])%mod[i])*(c/d)%mod[i])*mul,
mul=mul*mod[i]/gcd(mul,mod[i]),
ans%=mul;
else return -1;
}
return ans%mul;
}
int exlucas_jc(int n,int mod,int P=P)
{
if(!n)return 1;
int res(1);
for(int i(1);i<=P;++i)//不含因子mod[now]
if(i%mod)res=(res*i)%P;
res=qpow(res,n/P,P);
for(int i(1);i<=n%P;++i)if(i%mod)res=(res*i)%P;
return(res*(exlucas_jc(n/mod,mod,P)))%P;
}
int cal(int n,int m,int mod,int P=P)
{
int c1(exlucas_jc(n,mod,P));
int c2(exlucas_jc(m,mod,P));
int c3(exlucas_jc(n-m,mod,P));
int cnt(0);
for(int i(n);i;i/=mod)cnt+=(i/mod);
for(int i(m);i;i/=mod)cnt-=(i/mod);
for(int i(n-m);i;i/=mod)cnt-=(i/mod);
return(((qpow(mod,cnt,P)*c1)%P*inv_it(c2,P))%P*inv_it(c3,P))%P;
}
inline int crt(int x,int mod,int P)
{
return inv_it(P/mod,mod)*(P/mod)*x;
}
int exlucas(int n,int m,int now,int P)
{return(crt(cal(n,m,nth_mod[now],mod[now]),mod[now],P));}
int bsgs(int x,int y,int P=P)
{
if(!(x%P))return -1;
x%=P,y%=P;
if(y==1)return 0;
int Z(sqrt(P)+1);
int xx(y),yy;
hs::clean();
for(int i(0);i<Z;++i,xx=(xx*x)%P)hs::add(xx,i);
yy=qpow(x,Z),xx=1;
for(int i(1),k;i<=Z;++i)
{
xx=(xx*yy)%P,k=hs::find_x(xx);
if(k!=-1)return i*Z-k;
}
return -1;
}
}
namespace kill_tree
{
#define ls (p<<1)
#define rs (p<<1|1)
vector<int>e[N];
struct tt
{
int l,r;
long long add,sum,min;
}tr[N<<2];
int rt,r,cnt,head[N],f[N],d[N],root,b[N];
int siz[N],son[N],rk[N],top[N],dfn[N],cnm,a[N];
int pd[N];
void dfs1(int x,int fa)
{
d[x]=d[fa]+1;
f[x]=fa;
siz[x]=1;
for(int y:e[x])
{
if(y==fa)continue;
dfs1(y,x);
siz[x]+=siz[y];
if(siz[y]>siz[son[x]])son[x]=y;
}
}
void dfs2(int x,int t)
{
top[x]=t;
dfn[x]=++cnt;
rk[cnt]=x;
b[cnt]=a[x];
if(!son[x])return;
dfs2(son[x],t);
for(int y:e[x])
if(y!=f[x]&&y!=son[x])
dfs2(y,y);
}
int lca(int x,int y)
{
for(;top[x]!=top[y];x=f[top[x]])
if(d[top[x]]<d[top[y]])swap(x,y);
return d[x]>d[y]?y:x;
}
int find(int x,int y)
{
for(;top[x]!=top[y];x=f[top[x]])
{
if(d[top[x]]<d[top[y]])swap(x,y);
if(d[top[x]]==y)return top[x];
}
return d[x]<d[y]?son[x]:son[y];
}
void pushup(int p)
{
tr[p].sum=tr[ls].sum+tr[rs].sum;
tr[p].min=min(tr[ls].min,tr[rs].min);
}
void pushdown(int p)
{
if(tr[p].add)
tr[ls].sum+=tr[p].add*(tr[ls].r-tr[ls].l+1),
tr[rs].sum+=tr[p].add*(tr[rs].r-tr[rs].l+1),
tr[ls].min+=tr[p].add,tr[rs].min+=tr[p].add,
tr[ls].add+=tr[p].add,tr[rs].add+=tr[p].add,
tr[p].add=0;
}
void build(int p,int l,int r)
{
tr[p].l=l,tr[p].r=r;
if(l==r){tr[p].sum=tr[p].min=a[l];return;}
int mid=(l+r)>>1;
build(ls,l,mid),build(rs,mid+1,r);
pushup(p);
}
void update(int p,int l,int r,long long k)
{
if(l<=tr[p].l&&r>=tr[p].r)
{
tr[p].sum+=k*(tr[p].r-tr[p].l+1);
tr[p].min+=k;tr[p].add+=k;
return;
}
int mid=(tr[p].l+tr[p].r)>>1;
pushdown(p);
if(l<=mid)update(ls,l,r,k);
if(r>mid)update(rs,l,r,k);
pushup(p);
}
void update_path(int p,int v,long long k)
{
for(;top[p]!=top[v];p=f[top[p]])
{
if(d[top[p]]<d[top[v]])swap(p,v);
update(1,dfn[top[p]],dfn[p],k);
}
if(d[p]<d[v])swap(p,v);
update(1,dfn[v],dfn[p],k);//最后一段
}
void upd(int x,int y,long long z)
{
int l=lca(x,y);int r=f[l];
update(1,dfn[x],dfn[x],z),update(1,dfn[y],dfn[y],z),
update(1,dfn[l],dfn[l],~z+1),update(1,dfn[r],dfn[r],~z+1);
}
void update_tree(int p,long long k){update(1,dfn[p],dfn[p]+siz[p]-1,k);}
long long querysum(int p,int l,int r)
{
long long ans=0;
if(l<=tr[p].l&&r>=tr[p].r)return tr[p].sum;
pushdown(p);
int mid=(tr[p].l+tr[p].r)>>1;
while(l<=mid)ans+=querysum(ls,l,r);
if(r>mid)ans+=querysum(rs,l,r);
return ans;
}
long long querysum_path(int p,int v)
{
//p,v为旧点编号
//把树链剖分成若干个重链,重链在序列中编号连续
long long ans=0;
for(;top[p]!=top[v];p=f[top[p]])
{
if(d[top[p]]<d[top[v]])swap(p,v);
ans+=querysum(1,dfn[top[p]],dfn[p]);
}
if(d[p]<d[v])swap(p,v);
ans+=querysum(1,dfn[v],dfn[p]);
return ans;
}
long long querysum_tree(int x)
{
if(x==root)return querysum(1,1,n);
else
if(lca(x,root)!=x)
return querysum(1,dfn[x],dfn[x]+siz[x]-1);
else{int dson=find(x,root);return querysum(1,1,dfn[dson]-1),querysum(1,dfn[dson]+siz[dson],n);}
}
int querymin(int p,int l,int r)
{
int res=0x7f7f7f7f;
if(tr[p].l>=l&&tr[p].r<=r)return tr[p].min;
int mid=tr[p].l+tr[p].r>>1;
while(l<=mid)res=min(res,querymin(ls,l,r));
if(r>mid)res=min(res,querymin(rs,l,r));
return res;
}
#undef ls
#undef rs
}
/*namespace modui
{
int len,ans;
int a[50010];
int res,l,r,k;
int out[50010],cnt[50010];
struct aa{int l,r,id;}q[50010];
bool cmp(aa a,aa b)
{return (a.r/len==b.r/len)?a.l<b.l:a.r<b.r;}
void add(int x){ans+=(((++cnt[a[x]])<<1)-1);}
void del(int x){ans-=((--cnt[a[x]]<<1)+1);}
//左端点递增,每块内按照右端点排序
}*/
namespace MST
{
int f[10010],w;
struct aa{int x,y,w;}e[10010];
bool cmp(aa x,aa y){return x.w<y.w;}
int find(int x){if(x==f[x])return x;return f[x]=find(f[x]);}
void unionf(int x,int y){x=find(x),y=find(y);f[x]=y;}
}
void init_set()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
}
int ans=0x3f3f3f3f;
signed main()
{
init_set();
n=read();m=read();
for(int i(1);i<=m;++i)l=read(),r=read(),ans=min(ans,r-l+1);
for(int i(1);i<=n;++i)write(i%ans,' ');
flush();
return 0;
}
T5(校门外的树)
\(0pts\)
- 不仅没打出来, \(freopen\) 都没打对,所以肯定 \(0\) 分。
- 本来是道原题,之前就废了很长时间想,但是没想出来,比赛时想着 \(A\) 掉,一开始写线段树,但是线段树不知道怎么维护。之后想着暴力,分块吧。结果分块板子也没打对,忘了和线段树一样要有懒标记一样的东西。
- 其实本来暴力也能得点分,但是就是想打正解,所以一分没得,还浪费了很多时间。
- 可能学的少了也有点优势,因为他们会只想着暴力得点部分分,之后怎么也能拿到点分。但是本蒟蒻却没有部分分的意识(或者很少)。
思路
- \(~~~~~~\)
暴力者来 线\(~~~~~~~~~~~~~~~~~~\)神段\(~~~~~~~~~~~~~~~~~~\)犇树\(~~~~~~~~~~~~~~~~~~\)大解\(~~~~~~~~~~~~~~~~~~\)佬请\(~~~~~~~~~~~~~~~~~~\)勿往\(~~~~~~~~~~~~~~~~~~\)入他\(~~~~~~~~~~~~~~~~~~\)斯处\(~~~~~~~~~~~~~~~~~~\)门- 既然是分块,复杂度 \(O(n\sqrt n)\) 。实际测试大数据大概在 \(800ms\) 左右。(显然比三秒时限少)。
- 首先将树原有的高度存到前缀和 \(SUM\) 数组中,因为这些都是固定的,不会变。
- 对于修改生长速度,先看这幅图。
![image]() 显然绿色区域的面积是应该长高的高度,但是如果我们只维护生长速度,还想着只在询问的时候去现求高度,就会出现将红色区域的面积也算在内的情况。因此每次修改后,都需要再记录一下需要减去的高度。而这个高度很好求,设在第 \(t\) 天 增长速度增长了 \(k\) ,则需要减去的高度就是 \(kt\) 。很显然,从图上就能够看出来。
显然绿色区域的面积是应该长高的高度,但是如果我们只维护生长速度,还想着只在询问的时候去现求高度,就会出现将红色区域的面积也算在内的情况。因此每次修改后,都需要再记录一下需要减去的高度。而这个高度很好求,设在第 \(t\) 天 增长速度增长了 \(k\) ,则需要减去的高度就是 \(kt\) 。很显然,从图上就能够看出来。 - 对于查询操作,只需要将原高度加上增长高度乘天数,最后去掉多计算的高度,也就是 \(\large SUM_r-SUM_{l-1}+\sum\limits_{i=l}^rspeed_i-\sum\limits_{i=l}^rcut_i\) 。
代码
#include<bits/stdc++.h>
#define N (500010)
#define int unsigned long long
#define sort stable_sort
using namespace std;
namespace IO
{
#define ll unsigned long long
const int MAX=1<<25;
char buf[MAX],*p1=buf,*p2=buf;
char obuf[MAX],*o=obuf;
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
//template<typename T>
//inline T read()
inline int read()
{
int x=0;bool f=1;
char c=gc();
for(;c<48||c>57;c=gc())if(c=='-')f=0;
for(;c>=48&&c<=57;c=gc())x=(x<<3)+(x<<1)+(c^48);
return f?x:~x+1;
}
void print(ll x){if(x>9)print(x/10);*o++=(x%10)+'0';}
void pit(ll x){if(x<0)*o++='-',x=~x+1;print(x);}
void write(ll x,char end){pit(x);*o++=end;}
void flush(){fwrite(obuf,o-obuf,1,stdout);}
#undef ll
}
using IO::read;using IO::write;using IO::flush;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x<y?x:y;}
inline void swap(int &x,int &y){int tmp=x;x=y;y=tmp;}
int n,m;
void init_set()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
}
int ans[500010],sum[500010],l,r,k,len;
int add[500010],spd[500010],sspd[500010];
int pos[500010],L[500010],R[500010];
int cut[500010],scut[500010],SUM[500010],itcut[500010];
void update(int l,int r,int k,int t)
{
int p(pos[l]),q(pos[r]);
if(p==q)
{
if(l==L[p]&&r==R[q])
{add[p]+=k,scut[p]+=k*t;return;}
for(int i(l);i<=r;++i)spd[i]+=k,cut[i]+=k*t;
sspd[p]+=k*(r-l+1);itcut[p]+=k*t*(r-l+1);
return;
}
for(int i(p+1);i<=q-1;++i)add[i]+=k,scut[i]+=k*t;
for(int i=l;i<=R[p];++i)spd[i]+=k,cut[i]+=k*t;
sspd[p]+=k*(R[p]-l+1);itcut[p]+=k*t*(R[p]-l+1);
for(int i(L[q]);i<=r;++i)spd[i]+=k,cut[i]+=k*t;
sspd[q]+=k*(r-L[q]+1);itcut[q]+=k*t*(r-L[q]+1);
}
int query(int l,int r,int t)
{
int p(pos[l]),q(pos[r]),res(SUM[r]-SUM[l-1]);
if(p==q)
{
if(l==L[p]&&r==R[q])
return(sspd[p]*t+add[p]*t*(r-l+1)-scut[p]*(r-l+1));
for(int i(l);i<=r;++i)res+=(spd[i]*t-cut[i]);
res+=add[p]*(r-l+1)*t-scut[q]*(r-l+1);
return res;
}
for(int i(p+1);i<=q-1;++i)
res+=(sspd[i]*t+add[i]*t*(R[i]-L[i]+1)-scut[i]*(R[i]-L[i]+1)-itcut[i]);
for(int i(l);i<=R[p];++i)res+=(spd[i]*t-cut[i]);
res+=add[p]*(R[p]-l+1)*t-scut[p]*(R[p]-l+1);
for(int i(L[q]);i<=r;++i)res+=(spd[i]*t-cut[i]);
res+=add[q]*(r-L[q]+1)*t-scut[q]*(r-L[q]+1);
return res;
}
signed main()
{
init_set();
n=read(),m=read();len=sqrt(n);
for(int i(1);i<=n;++i)
ans[i]=read(),spd[i]=read(),SUM[i]=SUM[i-1]+ans[i];
for(int i(1);i<=len;++i)L[i]=(i-1)*len+1,R[i]=i*len;
if(len*len!=n)L[len+1]=len*len+1,R[len+1]=n,++len;
for(int i(1);i<=len;++i)
for(int j(L[i]);j<=R[i];++j)
pos[j]=i,sspd[i]+=spd[j];
for(int t(1);t<=m;++t)
{
if(read()==1)
l=read(),r=read(),k=read(),
update(l,r,k,t);
else
l=read(),r=read(),
write(query(l,r,t),'\n');
}
flush();
return 0;
}
[T6]
\(0pts\)
- 这题烦人的就是修改,如果暴力将每个值都修改一遍,就有 \(O(n^2)\) 的复杂度。显然最后会变成 \(O(mn^2)\) 的复杂度。
- 显然可以通过树状数组来优化一下。二维树状数组可能是最先想到的,显然,二维树状数组并不好打,所以还要进一步简化。
- 那么如果是 \(n\) 个一维树状数组呢?那就可以简化到 \(O(mn\log n+n^2\log n)\) 。因为单次修改只需要 \(O(n\log n)\) , \(m\) 次修改后,单点查询需要 \(O(\log n)\) ,因此最终是 \(O(mn\log n+n^2\log n)\)
- 然后你会发现这个复杂度似乎过不去。
- 树状数组中很重要的思想就是差分,而如果我们直接差分,就可以用 \(O(n^2)\) 的时间复杂度解决此题。
代码
#include<bits/stdc++.h>
#define N (500010)
#define int long long
#define sort stable_sort
using namespace std;
namespace IO
{
#define ll long long
const int MAX=1<<25;
char buf[MAX],*p1=buf,*p2=buf;
char obuf[MAX],*o=obuf;
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
//template<typename T>
//inline T read()
inline int read()
{
int x=0;bool f=1;
char c=gc();
for(;c<48||c>57;c=gc())if(c=='-')f=0;
for(;c>=48&&c<=57;c=gc())x=(x<<3)+(x<<1)+(c^48);
return f?x:~x+1;
}
void print(ll x){if(x>9)print(x/10);*o++=(x%10)+'0';}
void pit(ll x){if(x<0)*o++='-',x=~x+1;print(x);}
void write(ll x,char end){pit(x);*o++=end;}
void flush(){fwrite(obuf,o-obuf,1,stdout);}
#undef ll
}
using IO::read;using IO::write;using IO::flush;
inline int min(int x,int y){return y&((y-x)>>31)|x&(~(y-x)>>31);}
inline int max(int x,int y){return x&((y-x)>>31)|y&(~(y-x)>>31);}
inline void swap(int &x,int &y){int tmp=x;x=y;y=tmp;}
int n,m;
void init_set()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
}
int cf[3010][3010],x,y,l,k,ans,sum[3010][3010];
signed main()
{
init_set();
n=read(),m=read();
for(int t(1);t<=m;++t)
{
x=read(),y=read(),l=read(),k=read();
for(int i(1);i<=l;++i)
cf[x+i-1][y]+=k,cf[x+i-1][y+i]-=k;
}
for(int i(1);i<=n;++i)
for(int j(1);j<=n;++j)
sum[i][j]=sum[i][j-1]+cf[i][j];
for(int i(1);i<=n;++i)
{
for(int j(1);j<=n;++j)
write(sum[i][j],' ');
*IO::o++='\n';
}
for(int i(1);i<=n;++i)
for(int j(1);j<=n;++j)
ans^=sum[i][j];
write(ans,' ');
flush();
return 0;
}
之前的OJ

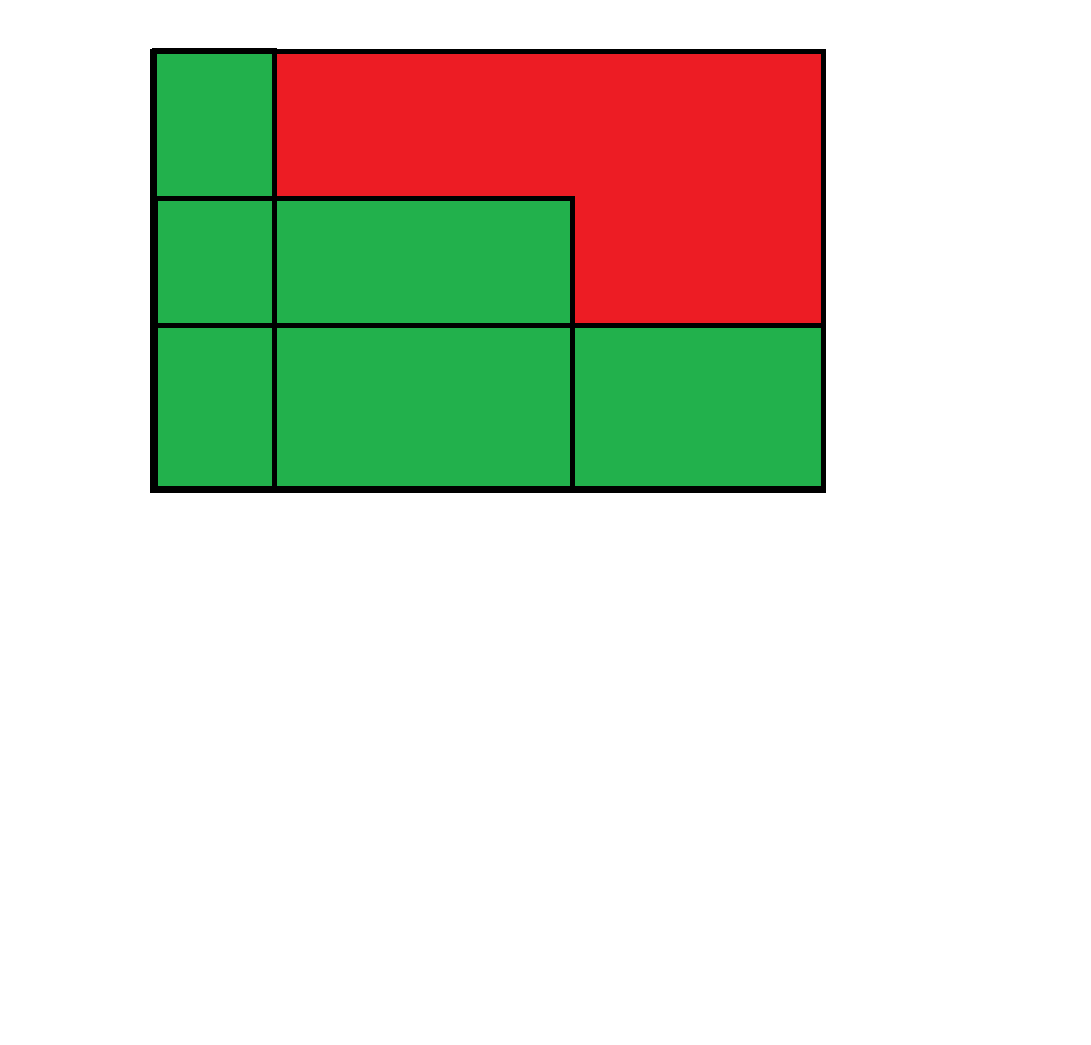 显然绿色区域的面积是应该长高的高度,但是如果我们只维护生长速度,还想着只在询问的时候去现求高度,就会出现将红色区域的面积也算在内的情况。因此每次修改后,都需要再记录一下需要减去的高度。而这个高度很好求,设在第
显然绿色区域的面积是应该长高的高度,但是如果我们只维护生长速度,还想着只在询问的时候去现求高度,就会出现将红色区域的面积也算在内的情况。因此每次修改后,都需要再记录一下需要减去的高度。而这个高度很好求,设在第 
 浙公网安备 33010602011771号
浙公网安备 33010602011771号