逻辑预算

概念

机器数只能以二进制方式表示，大类分为【无符号数】和【有符号数】

【无符号数】在机器数中没有符号，表示正数

【有符号数】在机器数中有符号，包含正数的其他数值，存在四种操作：【原码】【反码】【补码】【移码】

一、原码

最高位作为符号位进行正数和负数表示

剩余低位表示数值的绝对值

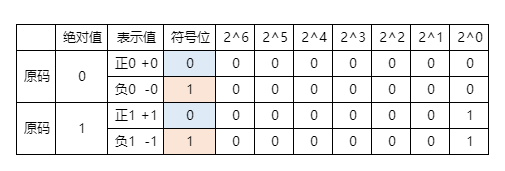
假设位数为3，则可以得知符号位1位和低位数值位2位

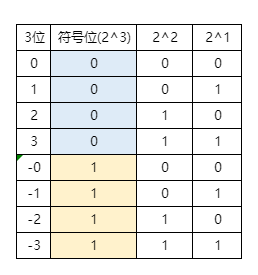
整数范围是 -3 到 3，转换公式为 -(2^N-1 -1)到 2^N-1 -1，N表示位数

表示的数值个数是7个，因为-0表示没有意义，转换公式为 2^N - 1

二、反码

1、正数的反码处理后还是正数

2、负数的反码处理是对低位数码的取反

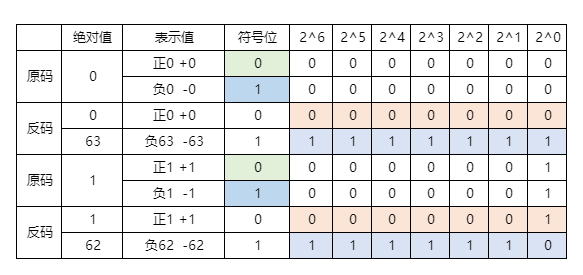
3、因为是对原码的取反，所以数值表示范围和表示个数与原码一致：

表示范围：【-(2^N-1 -1)到 2^N-1 -1】

表示个数：【2^N - 1】

三、补码

1、正数的补码处理还是正数

2、负数的补码处理是先反码后再对最低位 + 1

3、补码进位会使符号位进位

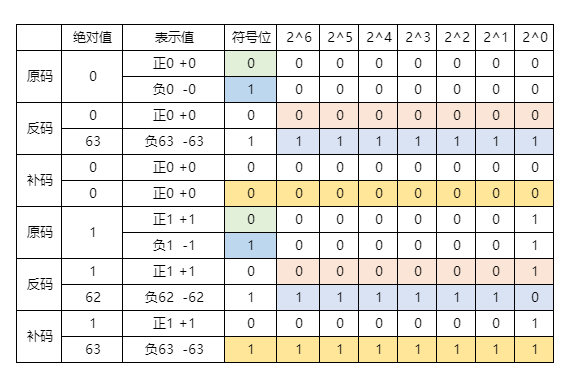
4、补码有【人为定义】的表示数值

其中N为3位时，100 不再认为是-0数值，而视为-4进行表示

同样N为8位时，1000 0000 视为-128进行表示

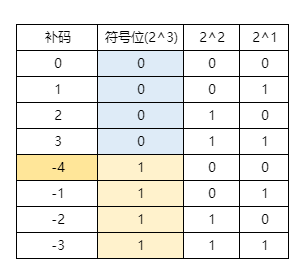
所以补码的表示范围相比原码，在负数范围多1个，而表示个数也多1个

表示范围：【-2^N-1到 2^N-1 -1】

表示个数：【2^N】

四、移码

1、移码，是对补码的符号位进行取反

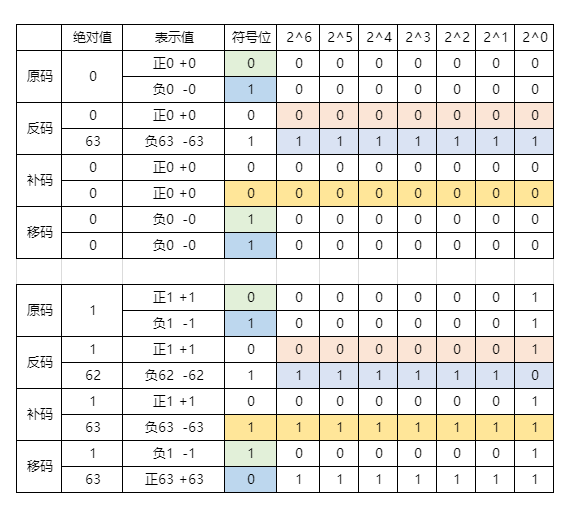
2、同样，基于补码的操作，移码是对符号位取反

所以表示范围和表示个数与补码一致

表示范围：【-2^N-1到 2^N-1 -1】

表示个数：【2^N】

五、定点小数的码制

可以参考第一篇进制转换：

https://www.cnblogs.com/mindzone/p/18417186

1、进制转换，小数部分是 -1、-2、... -N的位数计算

2、数值范围在大于-1和小于1的区间内

- 原码和反码的表示范围和表示个数

表示范围从 -(1 - 2^-(N-1)) 到 +(1 - 2^-(N-1))

表示个数 2^N - 1

- 补码处理人为规定 -1的补码的符号位为，其余数值位为0

表示范围从 -1 到 +(1 - 2^-(N-1))

表示个数 2^N

六、对照表

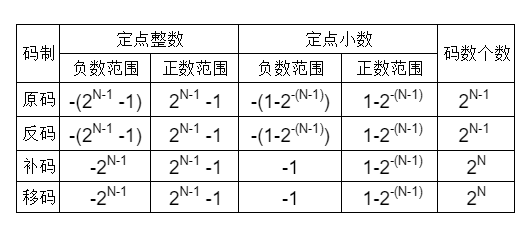
七、例题：

1、采用n位补码(包含-个符号位)表示数据，可以直接表示数值( )。

A、 2n
B、-2n
C、2n-1
D、-2n-1

解析思路：

假设N为3，则符号位为1，数值位为2

正数最大值为0111 也就是3

负数最大值为1000 也就是-4 【补码人为规定】

A选项 2的3次方为8，最大值3，所以错误

B选项 -2的3次方为-8，最大值-4，所以错误

C选项 2的3次方-1为7，最大值3，所以错误

D选项 -2的2次方-4，最大值-4，包含该数值，所以正确

2、如果“2X”的补码是“90H”，那么X的真值是()。

A、72
B、-56
C、56
D、111

解题思路：

X代表未知数，H表示90为十六进制表示数

1、转换90H为二进制表示数

90 -> 9%2 = 4(1), 4%2 = 2(0) , 2%2 = 1(0), 2%1 = 0(1)，0位无需计算，补位即可

所以2X的补码表示为 1001 0000

2、从补码转换成原码，过程是反补码 -> 反反码 ->得原码

补码是+1，则反补码是 -1

10010000 反补码 -1 退位为 10001111

反码是对负数的数值位取反操作，所有题型，默认最高位就是符号位

10001111 最高位是1所以需要按负数进行取反操作

3、原码转换需要记住符号位不参与进制转换

1【0001111】反反码后为 1【1110000】

1【1110000】转十进制为 -(2⁶ + 2⁵ + 2⁴) = -( 64 + 32 + 16 ) = -112

所以 2X = -112 ，X = -56，答案选B

4、从步骤2就可以知道原码是负数值，所以可以一眼看选项B即可

七、浮点数运算

N = 尾数 * 基数^{指数(阶码)}

浮点数运算步骤

- 1、对阶，阶码需要保持一致，小的阶码向大阶码一致

- 2、尾数计算

- 3、结果格式化

例如：

1.25 * 10⁶ + 1.255 * 10¹⁰

小阶码是6，大阶码是10，则需要转换成阶码10为准

则1.25对阶后是 0.000125 * 10¹⁰

为 0.000125 * 10¹⁰ + 1.255 * 10¹⁰= （0.000125 + 1.255）* 10¹⁰

得到 1.255125 * 10¹⁰

其他特点：

1、一般尾数用补码，阶码用移码（IEE754的尾数支持用原码表示）
2、阶码的位数决定数的表示范围，位数越多范围越大
3、尾数的位数决定数的有效精度，位数越多精度越高
4、对阶时，小数向大数看齐
5、对阶是通过较小数的尾数右移实现的

数符是尾数部分的符号位

阶符是阶码的符号位，决定整个码值是整数还是小数，例如 1 * 2³ = 8 和 1 * 2^-3 = 0.125

例题

设16位浮点数，其中阶符1位、阶码值6位、数符1位、尾数8位。若阶码用移码表示，尾数用补码表示，则该浮点数所能表示的数值范围是()。
A.-2⁶⁴~ (1-2^-8) 2⁶⁴
B. -2⁶³~ (1-2^-8) 2⁶³
C.- (1-2^-8) 2⁶⁴~ (1-2^-8) 2⁶⁴
D. - (1-2^-8) 2⁶³~ (1-2^-8) 2⁶³

解题思路：

N = 尾数 * 基数^{指数(阶码)}

1、阶码用移码表示：1【00000】最小值为 -64 （人为规定），0【111111】最大值为63

阶码能表示的数值范围是 2^-64 到 2⁶³，所以可以排除AC选项

2、尾数用补码表示：补码的最小值为-1

B和D的结束范围一致，但是起始范围不一样

-2⁶³和- (1-2^-8) ，- (1-2^-8) 解除括号为 -1 + 2^-8

则可以显然看出起始范围 -2⁶³ 是要大于-1 + 2^-8的

所以答案选B

八、逻辑运算

括号 > 逻辑运算 > 算术运算 > 关系运算 > 赋值运算

要判断字长为16位的整数a的低四位是否全为0,则()。
A、将a与0x000F进行"逻辑与"运算，然后判断运算结果是否等于0
B、将a与0x000F进行"逻辑或"运算，然后判断运算结果是否等于F
C、将a与0x000F进行"逻辑异或"运算，然后判断运算结果是否等于0
D、将a与0x000F 进行"逻辑与"运算，然后判断运算结果是否等于F

解题思路

【全为0】要求逻辑与运算，故BC选项排除

【为0】要求运算结果为是否等于0，故D选项排除，答案选A

对布尔表达式进行短路求值是指:无须对表达式中所有操作数或运算符进行计算就可确定表达式的值。
对于表达式"a or ((< d) andb)”，( )时可进行短路计算。
A、d为true
B、a为true
C、b为true
D、c为true