机器学习第六周--机器学习重要概念补充

一.sklearn中的Pipeline串联用法

 

    Python搭建机器学习模型时，Pipeline是一个加快效率的方法，主要介绍学习串联用法。Pipeline处理机制就像是把所有模型塞到一个管子里，然后依次对数据进行处理，得到最终的分类结果，例如模型一可以是一个数据标准化处理，模型二可以是特征选择模型或者特征提取模型，模型三可以是一个分类器或者预测模型。Pipeline就是把这三个模型（模型不一定非要三个，根据自己实际需要）塞到管子里合并成一个模型调用，其中最后一个模型一定要是估计器，例如分类器。

 

     sklearn中Pipeline调用方法如下：

#模型串联
pip=Pipeline(
              [                                #所有模型写进列表内
                （‘模型一名称’,模型一调用）,    #模型名称可以自己命名
                （‘模型二名称’,模型二调用）,
                （‘模型三名称’, 模型三调用）
              ]
            )
 
#模型调用
model=pip.fit(x,y)

   pie函数可以把多个模型按顺序打包在一起，输入的数据集经过模型的处理后，输出的结果作为下一步的输入，，最后一步的估计器对数据进行分类或者其他处理。除了最后一个模型外，其他模型都必须实现'fit()'和'transform()'方法， 最后一个模型需要实现fit()方法即可。当训练样本数据送进pip进行处理时， 它会逐个调用模型的fit()和transform()方法，然后用最后一个模型的fit()方法来进行分类或者其他处理。

  案例代码实现。

#导入数据库，使用sklearn库中的数据
from sklearn import datasets
digits=datasets.load_digits()
digits.data

#数据可视化
import pylab as pl
pl.gray() #灰度化图片
pl.figure(figsize=(3,3))
pl.matshow(digits.images[1])#显示图片
pl.show()

#数据拆分训练集和测试集
from sklearn.cross_validation import train_test_split
x_train,x_test,y_train,y_test=train_test_split(digits.data,digits.target,test_size=0.25,random_state=33)

 #模型串联
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

pip=Pipeline([('sc',StandardScaler()),('svc',LinearSVC())])

pip.fit(x_train,y_train)
y_predict=pip.predic
#结果分析
print(pip.score(x_test,y_test))

from sklearn.metrics import classification_report
print(classification_report(y_test,y_predict,target_names=digits.target_names.astype(str)))t(x_test)

二.模型误差

    模型误差 = 偏差 + 方差 + 不可避免的误差（噪音）。一般来说，随着模型复杂度的增加，方差会逐渐增大，偏差会逐渐减小，见下图：

 

 

    偏差衡量了模型的预测值与实际值之间的偏离关系。例如某模型的准确度为96%，则说明是低偏差；反之，如果准确度只有70%，则说明是高偏差。方差描述的是训练数据在不同迭代阶段的训练模型中，预测值的变化波动情况（或称之为离散情况）。从数学角度看，可以理解为每个预测值与预测均值差的平方和的再求平均数。通常在模型训练中，初始阶段模型复杂度不高，为低方差；随着训练量加大，模型逐步拟合训练数据，复杂度开始变高，此时方差会逐渐变高。可以通过下面的图片直观理解偏差和方差。

 

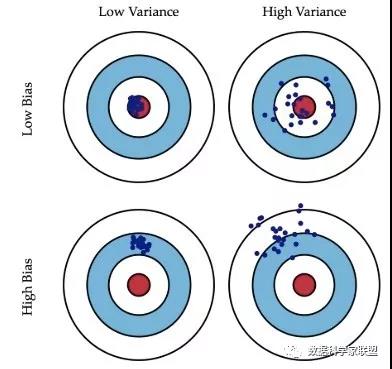
   如左下角的“打靶图”，假设我们的目标是中心的红点，所有的预测值都偏离了目标位置，这就是偏差；在右上角的“打靶图”中，预测值围绕着红色中心周围，没有大的偏差，但是整体太分散了，不集中，这就是方差。存在以下四种情况：

• 低偏差，低方差：这是训练的理想模型，此时蓝色点集基本落在靶心范围内，且数据离散程度小，基本在靶心范围内；
• 低偏差，高方差：这是深度学习面临的最大问题，过拟合了。也就是模型太贴合训练数据了，导致其泛化（或通用）能力差，若遇到测试集，则准确度下降的厉害；
• 高偏差，低方差：这往往是训练的初始阶段；
• 高偏差，高方差：这是训练最糟糕的情况，准确度差，数据的离散程度也差。

    一个模型有偏差，主要的原因可能是对问题本身的假设是不正确的，或者欠拟合。如：针对非线性的问题使用线性回归；或者采用的特征和问题完全没有关系，如用学生姓名预测考试成绩，就会导致高偏差。方差表现为数据的一点点扰动就会较大地影响模型。即模型没有完全学习到问题的本质，而学习到很多噪音。通常原因可能是使用的模型太复杂，如：使用高阶多项式回归，也就是过拟合。有一些算法天生就是高方差的算法，如kNN算法。非参数学习算法通常都是高方差，因为不对数据进行任何假设。有一些算法天生就是高偏差算法，如线性回归。参数学习算法通常都是高偏差算法，因为对数据有迹象。

    偏差和方差通常是矛盾的。降低偏差，会提高方差；降低方差，会提高偏差。这就需要在偏差和方差之间保持一个平衡。以多项式回归模型为例，我们可以选择不同的多项式的次数，来观察多项式次数对模型偏差和方差的影响。

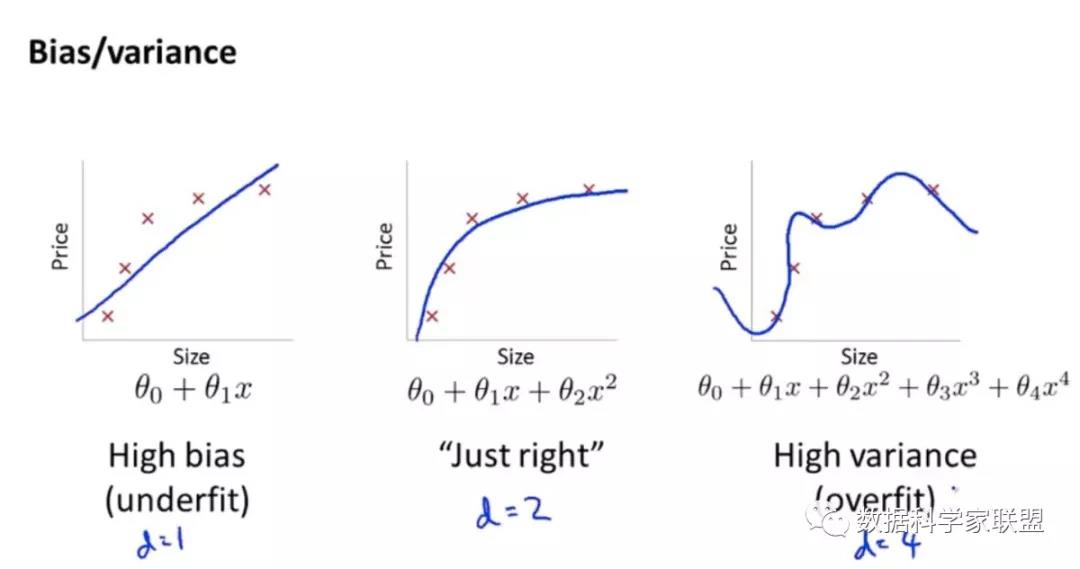
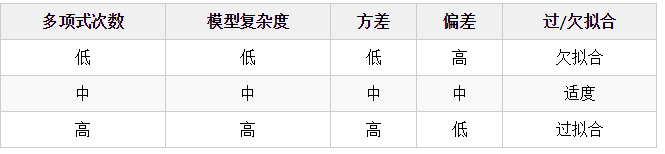
    下面是多项式次数对训练误差/测试误差的影响：

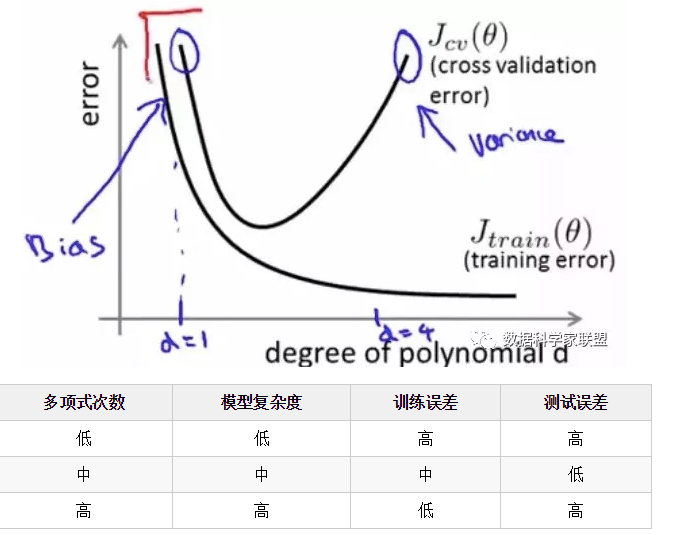
   我们知道偏差和方差是无法完全避免的，只能尽量减少其影响。

• 在避免偏差时，需尽量选择正确的模型，一个非线性问题而我们一直用线性模型去解决，那无论如何，高偏差是无法避免的。
• 有了正确的模型，我们还要慎重选择数据集的大小，通常数据集越大越好，但大到数据集已经对整体所有数据有了一定的代表性后，再多的数据已经不能提升模型了，反而会带来计算量的增加。而训练数据太小一定是不好的，这会带来过拟合，模型复杂度太高，方差很大，不同数据集训练出来的模型变化非常大。
• 最后，要选择合适的模型复杂度，复杂度高的模型通常对训练数据有很好的拟合能力。

三.模型正则化

    模型正则化（Regularization），对学习算法的修改，限制参数的大小，减少泛化误差而不是训练误差。我们在构造机器学习模型时，最终目的是让模型在面对新数据的时候，可以有很好的表现。当你用比较复杂的模型比如神经网络，去拟合数据时，很容易出现过拟合现象(训练集表现很好，测试集表现较差)，这会导致模型的泛化能力下降，这时候，我们就需要使用正则化，降低模型的复杂度。正则化的策略包括：约束和惩罚被设计为编码特定类型的先验知识 偏好简单模型 其他形式的正则化，如：集成的方法，即结合多个假说解释训练数据。在实践中，过于复杂的模型不一定包含数据的真实的生成过程，甚至也不包括近似过程，这意味着控制模型的复杂程度不是一个很好的方法，或者说不能很好的找到合适的模型的方法。实践中发现的最好的拟合模型通常是一个适当正则化的大型模型。

1.L1正则化

   所谓的L1正则化，就是在目标函数中加了L1范数这一项。使用L1正则化的模型叫做LASSO回归。 线性回归问题去怎样求最优解，其目标相当于使尽可能小。这也就是等同于求原始数据和使用参数预测的的均方误差尽可能的小：使尽可能小。

如果模型过拟合的话，参数就会非常大。为了限制参数，我们改变损失函数，加入模型正则化，即将其改为：使尽可能小。这样的话，要使尽可能小，就要综合考虑两项，对于第二项来说，是的绝对值，因此我们要考虑让尽可能小。这样参数就限制住了，曲线也就没有那么陡峭了，这就是一种模型正则化的基本原理。且该模型正则化的方式被称为“LASSO回归”。

 

    LASSO回归的全称是：Least Absolute Shrinkage and Selection Operator Regression.这里面有一个特征选择的部分，或者说L1正则化可以使得参数稀疏化，即得到的参数是一个稀疏矩阵。所谓稀疏性，说白了就是模型的很多参数是0。通常机器学习中特征数量很多，例如文本处理时，如果将一个词组（term）作为一个特征，那么特征数量会达到上万个（bigram）。在预测或分类时，那么多特征显然难以选择，但是如果代入这些特征得到的模型是一个稀疏模型，很多参数是0，表示只有少数特征对这个模型有贡献，绝大部分特征是没有贡献的，即使去掉对模型也没有什么影响，此时我们就可以只关注系数是非零值的特征。这相当于对模型进行了一次特征选择，只留下一些比较重要的特征，提高模型的泛化能力，降低过拟合的可能。

 

假设在二维参数空间中，损失函数的等高线如下图所示：

 

 

 此时，L1正则化为，对应的等高线是一个菱形（我们可以画出多个这样的菱形）：

 

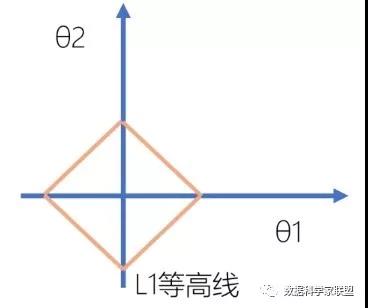
    首先来看一下不加L1正则的情况：我们使用梯度下降法去优化损失函数，随机选择一点，沿着梯度方向下降，得到一个近似的最优解M。

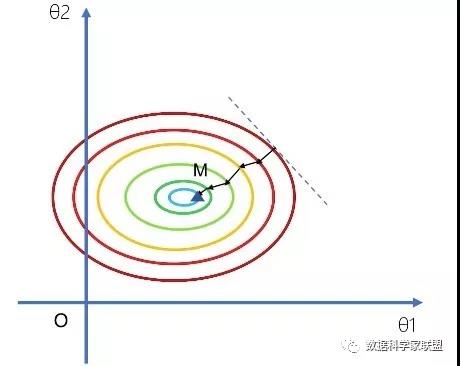
   下面加上L1正则，情况则会有所不同。P与Q两点在同一等高线上，即P与Q两个点的损失函数这一项上是相同的。但是OP的距离要大于OQ距离。

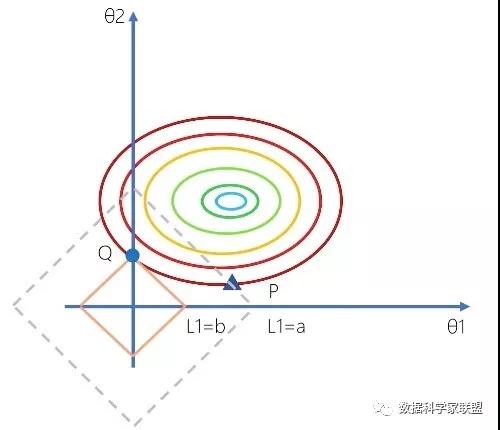
   因为点Q的L1范数小于点P的L1范数，因此我们更倾向于选择点Q，而不是点P。而如果选择点Q，在直角的顶点上，对应的参数Θ₁=0，这就体现了稀疏性。因此L1正则化会产生系数模型，好处是应用的特征比较小，模型更简单，运算更快。由此可见：加入L1正则项相当于倾向将参数向离原点近的方向去压缩。直观上来说，就是加上正则项，参数空间会被缩小，意味着模型的复杂度会变小。

LASSO回归代码模块

class sklearn.linear_model.Lasso(

alpha = 1.0, fit_intercept = True, normalize = False, copy_X = True precompute = False : 是否使用预计算的Gram矩阵加速拟合 max_iter = 1000, tol = 0.0001 warm_start = False : 是否使用上一次的模型拟合结果作为本次初始值 positive = False : 系数值是否必须非负 random_state = None selection = 'cyclic' : 随机更新系数还是按顺序更新，设为'random'可加速拟合

)

2.L2正则化

   当回归系数矩阵中X不是列满秩矩阵时，即特征数n比样本数m还多，则X.T*X的行列式为0，逆不存在。或者X的某些列的线性相关比较大时，则X.T*X的行列式接近0，X.T*X为病态矩阵（接近于奇异），此时计算其逆矩阵误差会很大，传统的最小二乘法缺乏稳定性与可靠性。为了解决这个问题，统计学家引入岭回归的概念。简单来说，岭回归就是在矩阵X.T*X上加上一个λI从而使矩阵非奇异，进而能对 X.T*X + λI 求逆。其中，λ是一个用户给定的参数，I是一个nxn的单位矩阵（像是在0构成的平面上有条1组成的“岭”），这种处理方式被称作“岭回归”。

 在二维参数空间中，L2正则项为：L2=Θ1²+Θ₂²+。即L2等高线是一个个的同心圆。

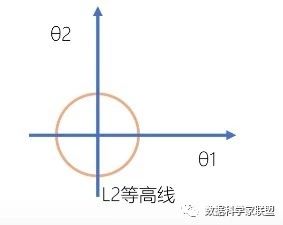
   二维平面下L2正则化的函数图形是个圆，与方形相比，被磨去了棱角。因此等高线与损失函数相交于点P,Q时，Θ₁,Θ₂都不为0，但是仍然比较靠近坐标轴，但得到的不是稀疏解。因此这也就是我们说的，L2范数能让解比较小（靠近0），但是比较平滑（不等于0）且不具有稀疏性。

 

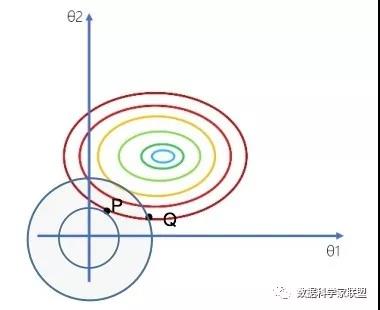
拟合岭回归模型Python代码实现

class sklearn.linear_model.Ridge(

alpha = 1.0 : 模型惩罚项的系数，正数，越大惩罚力度越强 fit_intercept = True, normalize = False, copy_X = True max_iter = None : 容许的最大迭代次数 tol = 0.001 : 收敛标准 solver='auto' : 收敛方法 {'auto', 'svd', 'cholesky', 'lsqr', 'sparse_cg', 'sag','saga'} random_state = None : 伪随机种子的数值

)

注意：岭回归也可以用于分类模型，对应的方法为sklearn.linear_model.RidgeClassifier

以上是第六周的学习内容，供之后参考使用。