机器学习第二周-模型评价指标（II）

Python代码实现

一·分类模型

    1.sklearn.metrics中包含常用的评价指标：   

#准确率
accuracy_score(y_true, y_pred, normalize=True, sample_weight=None)

 

   参数：

• y_true ：验证集
• y_pred ：分类器的返回值
• normalize：默认值为True，返回正确分类的比例；如果为False，返回正确分类的样本数

#精确率
precision_score(y_true, y_pred, labels=None, pos_label=1, average=’binary’, sample_weight=None)
#召回率
recall_score(y_true, y_pred, labels=None, pos_label=1, average=’binary’, sample_weight=None)
#F1
f1_score(y_true, y_pred, labels=None, pos_label=1, average=’binary’, sample_weight=None)

   参数：

• average : string, [None, ‘micro’, ‘macro’(default), ‘samples’, ‘weighted’]
• 将一个二分类matrics拓展到多分类或多标签问题时，我们可以将数据看成多个二分类问题的集合，每个类都是一个二分类。接着，我们可以通过跨多个分类计算每个二分类metrics得分的均值，这在一些情况下很有用。你可以使用average参数来指定。
• macro：计算二分类metrics的均值，为每个类给出相同权重的分值。当小类很重要时会出问题，因为该macro-averging方法是对性能的平均。另一方面，该方法假设所有分类都是一样重要的，因此macro-averaging方法会对小类的性能影响很大。
• weighted:对于不均衡数量的类来说，计算二分类metrics的平均，通过在每个类的score上进行加权实现。
• micro：给出了每个样本类以及它对整个metrics的贡献的pair（sample-weight），而非对整个类的metrics求和，它会每个类的metrics上的权重及因子进行求和，来计算整个份额。Micro-averaging方法在多标签（multilabel）问题中设置，包含多分类，此时，大类将被忽略。
• samples：应用在multilabel问题上。它不会计算每个类，相反，它会在评估数据中，通过计算真实类和预测类的差异的metrics，来求平均（sample_weight-weighted）
• average：average=None将返回一个数组，它包含了每个类的得分。

   接上篇文章的案例实践代码如下：

# 读取相应的库
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
import numpy as np

# 读取数据 X, y
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 把数据分成训练数据和测试数据
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=20)

# 构建KNN模型， K值为3、 并做训练
clf = KNeighborsClassifier(n_neighbors=3)
clf.fit(X_train, y_train)

# 计算准确率
from sklearn.metrics import accuracy_score
correct = np.count_nonzero((clf.predict(X_test)==y_test)==True)
print ("Accuracy is: %.3f" %(correct/len(X_test))) # Accuracy is: # output：0.921
# 把鸢尾花识别转换为二分类问题
y_train_binary = y_train.copy() #备份训练集的预测值y
y_test_binary = y_test.copy() #备份测试集的预测值y
#y值不是1就将其赋值为0，也就是预测值y只可能是1和0，把原来的三分类问题转成了2分类问题。
y_train_binary[y_train_binary != 1] = 0
y_test_binary[y_test_binary != 1] = 0
# 用KNN进行学习
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train_binary)
y_pred = knn.predict(X_test)
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
# 准确率
print('准确率：{:.3f}'.format(accuracy_score(y_test_binary, y_pred)))
# 精确率
print('精确率：{:.3f}'.format(precision_score(y_test_binary, y_pred)))
# 召回率
print('召回率：{:.3f}'.format(recall_score(y_test_binary, y_pred)))
# F1值
print('F1值：{:.3f}'.format(f1_score(y_test_binary, y_pred)))
#output  准确率：0.921
#output 精确率：0.867
#output 召回率：0.929
#output F1值：0.897

2、sklearn关于P-R曲线的函数 

1）求PR曲线的Recall值和Precision值 precision_recall_curve()

sklearn.metrics.precision_recall_curve(y_true, probas_pred, pos_label=None, sample_weight=None)

   AP的计算，此处参考的是PASCAL VOC CHALLENGE的2010年之前计算方法。首先设定一组阈值，[0, 0.1, 0.2, …, 1]。然后对于recall大于每一个阈值（比如recall>0.3），我们都会得到一个对应的最大precision。这样，我们就计算出了11个precision。AP即为这11个precision的平均值。这种方法英文叫做11-point interpolated average precision。​

  当然PASCAL VOC CHALLENGE自2010年后就换了另一种计算方法。新的计算方法假设这N个样本中有M个正例，那么我们会得到M个recall值（1/M, 2/M, ..., M/M）,对于每个recall值r，我们可以计算出对应（r' >= r）的最大precision，然后对这M个precision值取平均即得到最后的AP值。

2）如何用sklearn绘制PR曲线 

from sklearn.metrics import precision_recall_curve,average_precision_score
import matplotlib.pyplot as plt
precision, recall, _ = precision_recall_curve(y_test_binary, y_pred)
plt.step(recall, precision, color='b', alpha=0.2,where='post')
plt.fill_between(recall, precision, step='post', alpha=0.2, color='b')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.0])
plt.title('2-class Precision-Recall curve: AP={:.3f}'.format(average_precision_score(y_test_binary, y_pred)))

3、sklearn关于ROC曲线的函数 

1） roc_curve() 求fpr和tpr的值

 

sklearn.metrics.roc_curve(y_true, y_score, pos_label=None, sample_weight=None, drop_intermediate=True)

 

2）roc_auc_score() 求AUC值

roc_auc_score(y_true, y_score, average=’macro’, sample_weight=None)

3）如何绘制ROC曲线  

import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle
from sklearn import svm, datasets
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier
from scipy import interp
# Import some data to play with
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Binarize the output
y = label_binarize(y, classes=[0, 1, 2])
n_classes = y.shape[1]
# Add noisy features to make the problem harder
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]
# shuffle and split training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.5,random_state=0)
# Learn to predict each class against the other
classifier = OneVsRestClassifier(svm.SVC(kernel='linear', probability=True,random_state=random_state))
y_score = classifier.fit(X_train, y_train).decision_function(X_test)
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])

# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
plt.figure()
lw = 2
plt.plot(fpr[2], tpr[2], color='darkorange',lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

 

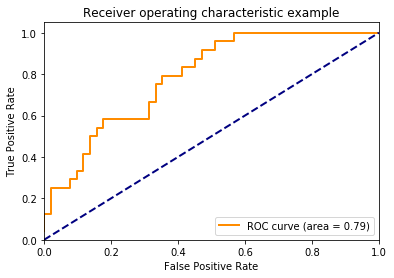
4、在sklearn使用混淆矩阵

得到混淆矩阵confusion_matrix()

 

sklearn.metrics.confusion_matrix(y_true, y_pred, labels=None, sample_weight=None)

 

参数：

• • y_true：真实因变量值
  • y_pred：预测因变量值
  • labels：矩阵的标签列表索引顺序
  • sample_weight：样本权重

输出：
一个矩阵，shape=[y中的类型数，y中的类型数]

二·回归模型

"""
# 利用 diabetes数据集来学习线性回归  
# diabetes 是一个关于糖尿病的数据集， 该数据集包括442个病人的生理数据及一年以后的病情发展情况。   
# 数据集中的特征值总共10项, 如下:  
    # 年龄  
    # 性别  
    #体质指数  
    #血压  
    #s1,s2,s3,s4,s4,s6  (六种血清的化验数据)  
    #但请注意，以上的数据是经过特殊处理， 10个数据中的每个都做了均值中心化处理，然后又用标准差乘以个体数量调整了数值范围。
    #验证就会发现任何一列的所有数值平方和为1.   
"""
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# Load the diabetes dataset
diabetes = datasets.load_diabetes()  
# Use only one feature  
# 增加一个维度，得到一个体质指数数组[[1],[2],...[442]]
diabetes_X = diabetes.data[:, np.newaxis,2]
print(diabetes_X) 
# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
# Split the targets into training/testing sets
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)
# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)
# The coefficients  
# 查看相关系数 
print('Coefficients: \n', regr.coef_)
#output Coefficients:   [938.23786125]
# The mean squared error  
# 均方差
# 查看残差平方的均值(mean square error,MSE) 
print("Mean squared error: %.2f"
      % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# output Mean squared error: 2548.07
# Explained variance score: 1 is perfect prediction 
#  R2 决定系数（拟合优度）
# 模型越好：r2→1
# 模型越差：r2→0
print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))
#output Variance score: 0.47
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()