机器学习第一周-KNN算法

一、KNN算法简介

    KNN即K近邻算法，待判别样本可以用离他距离最近的k个邻居标签属性来划分，因其训练样本集必须由带标签的样本组成，故它是一个有监督的机器学习算法，既可以用来做分类也可以用来做回归。下面通过图示案例加以理解。

      上图中，张三要参加一家公司的面试，通过各种渠道了解到一些工作年限和工资之间对应的关系，以及在此条件下他是否会得到offer的情况。来预测一下张三是否能够拿到这家公司的offer。当K-近邻中的K选择为1的时候，张三拿不到offer。

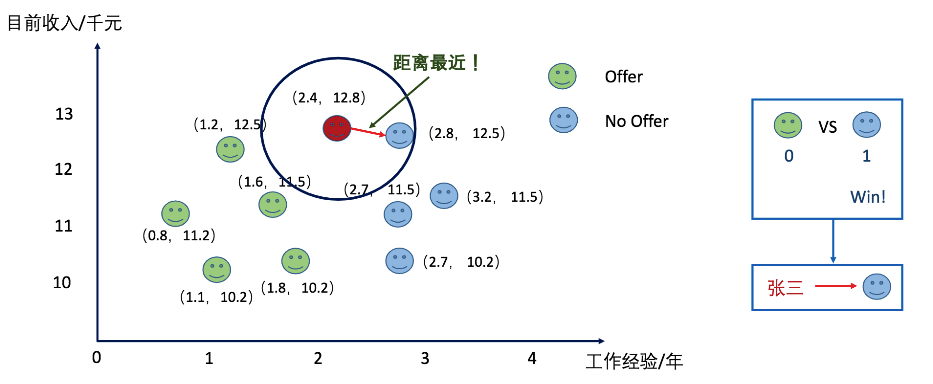
   当把K值设置为3的时候，张三拿到了offer。

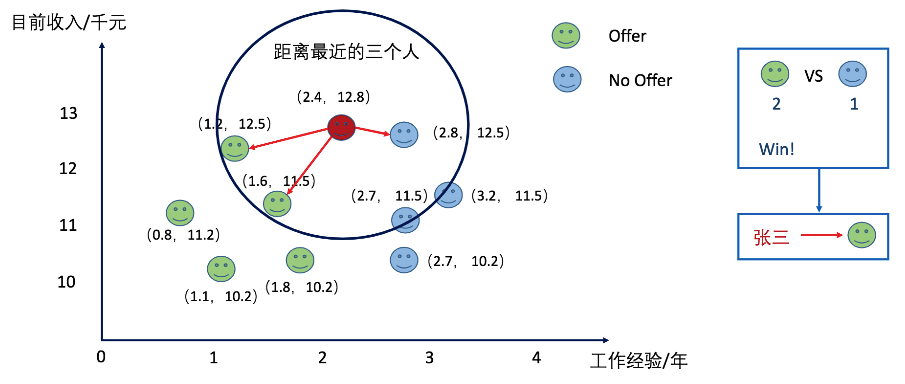
    而当我们将K值设置为5的时候呢？张三又被分类到了拿不到offer的类别上了。

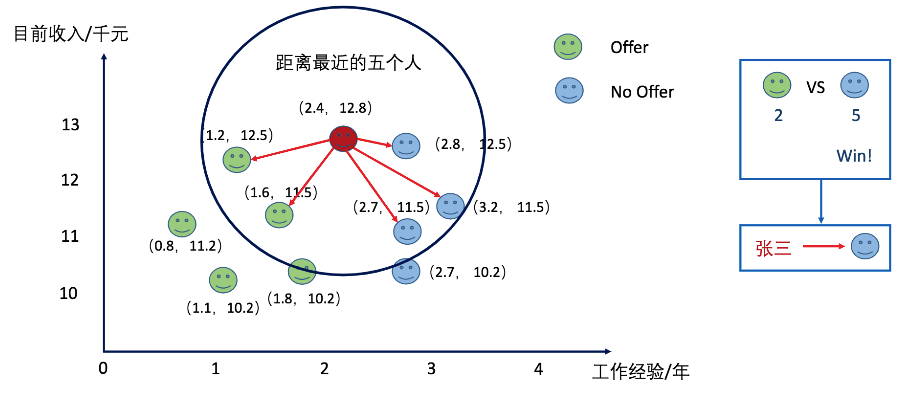
    上面的案例形象地展示了KNN算法，其核心思想是未标记的样本类别，由距离他最近的K个邻居投票来决定。KNN算法理论成熟，简单粗暴，既可以用来做分类（天然支持多分类），也可以用来做回归。并且与朴素贝叶斯之类的算法相比，由于其对数据没有假设，因此准确度高，对异常点不敏感。

二、KNN算法原理及实现流程

   KNN算法是指在一个给定的类别标签已知的训练样本集中，输入待判类别新样本后，将新的数据的每个特征与样本集中数据对应的特征进行比较，然后提取样本最相似的k个数据(最近邻)的分类标签，通过多数表决等方式进行预测。即选择k个最相似数据中出现次数最多的分类标签，作为新样本的标签分类。

   KNN算法可简化为“找邻居+投票”，使用的模型，实际上是特征空间的划分。模型由三个基本要素决定，距离度量，K值及分类决策规则。其中两个样本点之间的距离反映了相似程度，一般使用欧氏距离来度量。

   kNN算法实现流程如下：

• 计算测试对象到训练集中每个对象的距离
• 按照距离的远近排序
• 选取与当前测试对象最近的k个训练对象，作为该测试对象的邻居
• 统计这k个邻居的类别频次
• k个邻居里频次最高的类别，即为测试对象的类别标签

三、KNN算法python实现

    1.自实现KNN算法

   打开Jupyter Notebook，创建Python3文件。根据KNN算法实现流程，自实现代码如下：

from sklearn import datasets #sklaern自带的小的数据集
from collections import Counter  # 为了做投票,找出票数最多的n个元素，返回的是一个列表，列表中的每个元素是一个元组，元组中第一个元素是对应的元素是谁，第二个元素是频次
from sklearn.model_selection import train_test_split #交叉验证
import numpy as np  #数学与统计函数
iris = datasets.load_iris() #载入鸢尾花 数据集,存入变量iris中
iris.keys()  #dict_keys(['target_names', 'data', 'DESCR', 'target', 'feature_names'])
X = iris.data
y = iris.target 
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=20) #x：所要划分的样本特征集 y：所要划分的样本结果 random_state：是随机数的种子，其实就是该组随机数的编号，在需要重复试验的时候，保证得到一组一样的随机数.
def euc_dis(instance1, instance2):  #自定义距离函数 计算两个样本instance1和instance2之间的欧式距离
    """
    instance1: 第一个样本， array型
    instance2: 第二个样本， array型

   """
    dist = np.sqrt(sum((instance1 - instance2)**2))
    return dist
def knn_classify(X, y, testInstance, k):  # 给定一个测试数据testInstance, 通过KNN算法来预测它的标签。
    """
    X: 训练数据的特征
    y: 训练数据的标签
    testInstance: 测试数据，这里假定一个测试数据 array型
    k: 选择多少个neighbors? 
    """
    #  返回testInstance的预测标签 = {0,1,2}
    distances = [euc_dis(x, testInstance) for x in X]
    kneighbors = np.argsort(distances)[:k]  #对一个数组进行排序，返回的是相应的排序后结果的k个邻居对应的标签索引
    count = Counter(y[kneighbors])  
    return count.most_common()[0][0]  
# 预测结果  
predictions = [knn_classify(X_train, y_train, data, 3) for data in X_test]
correct = np.count_nonzero((predictions==y_test)==True)
print ("Accuracy is: %.3f" %(correct/len(X_test)))  #Accuracy is: 0.921

 2.sklearn中的KNN

  对于机器学习来流程是：训练数据集 -> 机器学习算法 -fit-> 模型 输入样例 -> 模型 -predict-> 输出结果；因kNN算法没有模型，模型其实就是训练数据集，训练预测的过程就是求k近邻。使用sklearn中已经封装好的kNN库也可以直接实现，操作简单。

# 读取相应的库
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
import numpy as np

# 读取数据 X, y
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 把数据分成训练数据和测试数据
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=20)

# 构建KNN模型， K值为3、 并做训练
clf = KNeighborsClassifier(n_neighbors=3)
clf.fit(X_train, y_train)

# 计算准确率
from sklearn.metrics import accuracy_score
correct = np.count_nonzero((clf.predict(X_test)==y_test)==True)
print ("Accuracy is: %.3f" %(correct/len(X_test))) # Accuracy is: 0.921

  预测结果一样，Accuracy is: 0.921。

  其中该模块涉及的参数如下：

 

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, weights=’uniform’, algorithm=’auto’, leaf_size=30, p=2, metric=’minkowski’, metric_params=None, n_jobs=None, **kwargs)

参数说明：

•  n_neighbors: int,可选参数(默认为 5)。用于kneighbors查询的默认邻居的数量
•  weight（权重）: str or callable(自定义类型), 可选参数(默认为 ‘uniform’)。用于预测的权重参数，可选参数如下：
  • uniform : 统一的权重. 在每一个邻居区域里的点的权重都是一样的。
  • distance: 权重点等于他们距离的倒数。使用此函数，更近的邻居对于所预测的点的影响更大。
  • [callable]: 一个用户自定义的方法，此方法接收一个距离的数组，然后返回一个相同形状并且包含权重的数组。
• algorithm（算法）: {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, 可选参数（默认为 'auto'）。计算最近邻居用的算法：
  • ball_tree 使用算法BallTree
  • kd_tree   使用算法KDTree
  • brute     使用暴力搜索
  • auto      会基于传入fit方法的内容，选择最合适的算法。注意 : 如果传入fit方法的输入是稀疏的，将会重载参数设置，直接使用暴力搜索。

• leaf_size(叶子数量) ：int,可选参数(默认为 30)。传入BallTree或者KDTree算法的叶子数量。此参数会影响构建、查询BallTree或者KDTree的速度，以及存储BallTree或者KDTree所需要的内存大小。此可选参数根据是否是问题所需选择性使用。

• P：integer, 可选参数(默认为 2)。用于Minkowski metric（闵可夫斯基空间）的超参数。p = 1, 相当于使用曼哈顿距离，p = 2, 相当于使用欧几里得距离]，对于任何 p ，使用的是闵可夫斯基空间。
• metric(矩阵)： string or callable, 默认为 ‘minkowski’。用于树的距离矩阵。默认为闵可夫斯基空间，如果和p=2一块使用相当于使用标准欧几里得矩阵. 所有可用的矩阵列表请查询 DistanceMetric 的文档。
• metric_params（矩阵参数）: dict, 可选参数(默认为 None)。给矩阵方法使用的其他的关键词参数。
• n_jobs: int, 可选参数(默认为 1)。用于搜索邻居的，可并行运行的任务数量。如果为-1, 任务数量设置为CPU核的数量。不会影响fit

 

  参数一般分为模型参数和超级参数。模型参数是需要我们通过不断的调整模型和超参数训练得到的最佳参数,而超参数则是我们人为手动设定的值。像在KNN中超参数就是K的值。关于K的选择,我们到底应该怎么去选择K的大小比较合适呢？答案是交叉验证。交叉验证指的是将训练数据集进一步分成训练数据和验证数据，选择在验证数据里面最好的超参数组合。交叉验证或者通俗一点的说法就是调参。可以通过交叉验证的方式，选择一组最好的K值作为模型最终的K值。

四、KNN算法需注意的几点

   1、特征的归一化

 

　　在进行距离计算的时候，某个特征的数值会特别的大，计算欧式距离的时，其他的特征的值的影响就会非常的小被大数给覆盖掉了。所以需要进行特征的归一化处理。

 

　　2、KD-Tree处理大数据量

 

　　一旦特征或者样本的数目特别多，KNN的时间复杂度将会非常的高。解决方法是利用KD-Tree这种方式解决时间复杂度问题。利用KD树可以将时间复杂度降到O(logD*N*N)。D是维度数，N是样本数。但是这样维度很多的话那么时间复杂度还是非常的高，所以可以利用类似哈希算法解决高维空间问题，只不过该算法得到的解是近似解，不是完全解。会损失精确率。

 

　　3、赋值权重差异化样本的重要性

 

　　在计算距离的时，可针对不同的邻居使用不同的权重值，比如距离越近的邻居我们使用的权重值偏大，通过调整算法weights参数来设置。

 

以上为机器学习第一周，参考了学习资料之后整理的学习笔记，案例均实际操作过，供日后参考。