最小生成树——Prim算法与Kruskal算法

最小生成树概念:
连通图: 在一个无向图中,任意两个顶点之间都是可达的(有路径连通),则成该无向图为连通图。
生成树: 一个连通图的生成树是一个极小的连通子图,它含有图中的全部顶点,但只有构成一棵树的n-1条边。也就是说,无向图中连通n个顶点n-1条边就叫做生成树。
最小生成树: 构造连通图的最小代价生成树称为最小生成树,也就是说,所有的边加权后和最小的树。
Prim算法
Prim算法计算最小生成树的方法从一个结点开始使树一点点的成长。在每一步,都增加一个结点作为根,并连接这个结点作为边,也就是说每次增加一个一个结点和一条边,这样也就把相关联的顶点加到增长中的树上了。这个过程主要体现在“加点”,在算法进行的过程中,有一个已经添加到树上的顶点集,这个顶点集实际就是最小生成树的结点集合,其余顶点都作为选择,等待是否被加入集合。每次选择一个顶点,使得它和上一个顶点之间的代价最小,并把这条边加入到最小生成树中,把顶点加入到集合中。
下面通过图示来描述Prim算法的思想:
首先选择一个顶点作为起始,比如A,第一轮发现AC代价最小,那么就把AC边加入最小生成树,把A加入顶点集合;
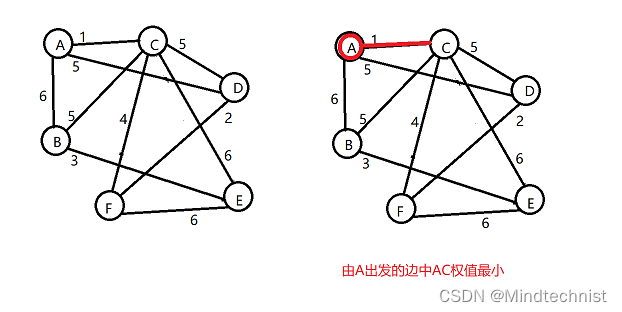
后面依次寻找最小代价边,直到全部顶点都加入到顶点集合。
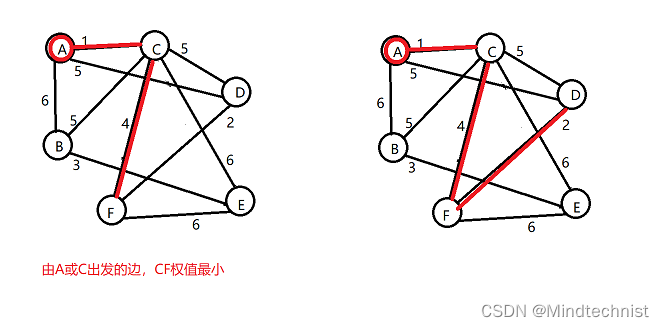
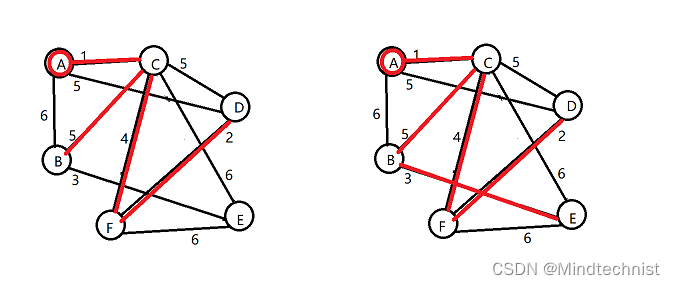
在程序中,通过一个最小代价标记,并一行一行的扫描来搜索最小代价边,下面来看具体代码。
首先我们定义一个图的数据类型,该数据类型包含图的顶点集合、邻接矩阵,顶点数和边数。另外宏定义两个常量,通过一个不可能的数比如65535来表示两个顶点之间没有边。
#define MAXVER 6 /*最大顶点个数*/
#define INFINITY 65535 /*代表无穷大*/
typedef struct _graph_type
{
char vertex[MAXVER]; /*存放顶点的数组*/
int arc[MAXVER][MAXVER]; /*邻接矩阵*/
int vertex_num; /*顶点数*/
int edge_num; /*边数*/
}graph_type;
Prim算法C语言实现
/*普利姆Prim算法求最小生成树*/
void mini_span_tree_prim(graph_type g)
{
int min = 0; /*保存最小权值*/
int k = 0; /*存放最小权值的顶点下标*/
int i = 0;
int j = 0;
int vertex_tree[MAXVER]; /*顶点下标 - 最小生成树的结点*/
int weight[MAXVER]; /*边的权值,置为0表示下标对应的顶点已加入最小生成树*/
weight[0] = 0; /*假设图标号为0的顶点是最小生成树的第一个结点*/
vertex_tree[0] = 0; /*加入第一个顶点*/
for(i = 1; i < g.vertex_num; i++) /*遍历图的所有顶点*/
{
weight[i] = g.arc[0][i]; /*把和0号顶点有边的边的权值存入数组*/
vertex_tree[i] = 0; /*初始化为0号顶点*/
}
for(i = 1; i < g.vertex_num; i++)
{
min = INFINITY; /*初始化最小权值为无穷大*/
j = 1;
k = 0;
while(j < g.vertex_num) /*遍历所有顶点*/
{
if(weight[j] != 0 && weight[j] < min)
{
/*如果权值不为0(未加入最小生成树),且权值小于最小权值min*/
min = weight[j]; /*更新当前最小权值*/
k = j; /*保存最小权值边所以来的顶点,第一次循环表示 (0, k)为0开始的所有边中权值最小的边*/
}
j++;
}
weight[k] = 0; /*将k的权值置为0,表示这个结点的最小权值已经找到了,同时顶点k已被加入最小生成树中*/
for(j = 1; j < vertex_num; j++)
{
if(weight[j] != 0 && g.arc[k][j] < weight[j])
{
/*如果j没有加入最小生成树,且邻接矩阵第k行相应权值小于weigh记录的最小权值*/
weight[j] = g.arc[k][j]; /*更新weight*/
vertex_tree[j] = k; /*把k加入到最小生成树*/
}
}
}
}
Kruskal算法
Prim算法是以某个顶点开始,逐步寻找各个顶点上最小权值的边,这样一步步来构建最小生成树。第二种贪心策略是连续地按照最小的权选择边,并且当所选的边不产生回路时就把它作为取定的边。
在形式上Kruskal算法是在处理一个森林,开始的时候,存在n棵单结点的树,每次添加一条边把两棵树合并成一棵树,当算法终止时剩下的一棵树就是最小生成树。
假设图和上面一样
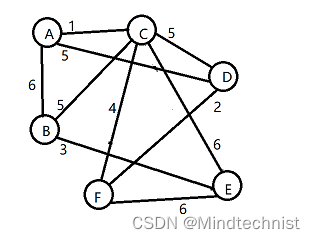
首先我们得到一张表,每条边按权值从小到大排序
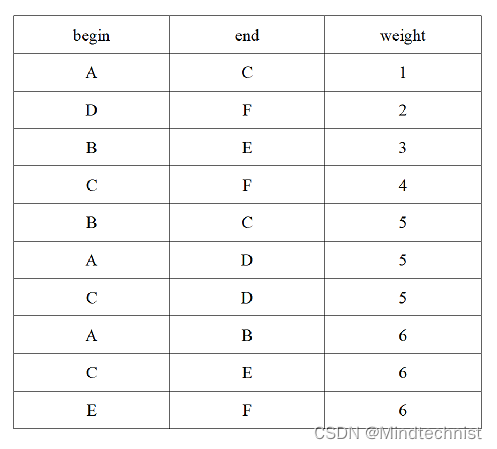
然后开始加边,优先选择权值小的边
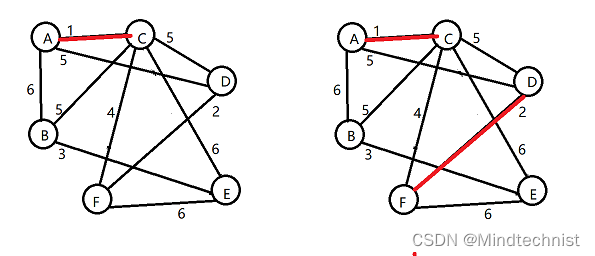
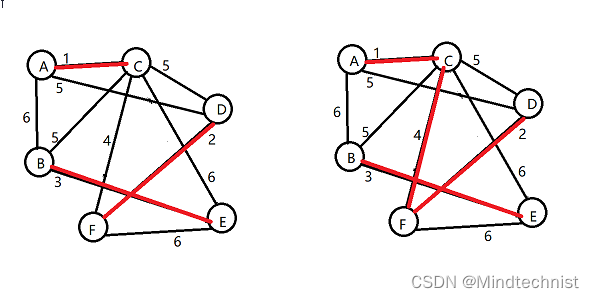
加最后一条边,得到最小生成树,和Prim算法得到的一样
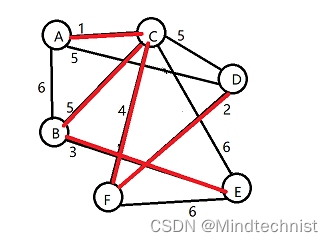
Kruskal算法C语言实现
#define MAXedge_type 20 /*最大边数*/
#define MAXVEX 20 /*最大顶点数*/
#define INFINITY 65535 /*无穷大*/
typedef struct
{
int arc[MAXVEX][MAXVEX];
int vertex_num;
int edge_type_num;
}graph_type;
typedef struct
{
int begin;
int end;
int weight;
}edge_type; /* 对边集数组edge_type结构的定义 */
/* 交换权值 以及头和尾 */
void Swapn(edge_type *edge_types,int i, int j)
{
int temp;
temp = edge_types[i].begin;
edge_types[i].begin = edge_types[j].begin;
edge_types[j].begin = temp;
temp = edge_types[i].end;
edge_types[i].end = edge_types[j].end;
edge_types[j].end = temp;
temp = edge_types[i].weight;
edge_types[i].weight = edge_types[j].weight;
edge_types[j].weight = temp;
}
/* 对权值进行排序 */
void sort(edge_type edge_types[], graph_type *G)
{
int i, j;
for ( i = 0; i < G->edge_type_num; i++)
{
for ( j = i + 1; j < G->edge_type_num; j++)
{
if (edge_types[i].weight > edge_types[j].weight)
{
Swapn(edge_types, i, j);
}
}
}
printf("权排序之后的为:\n");
for (i = 0; i < G->edge_type_num; i++)
{
printf("(%d, %d) %d\n", edge_types[i].begin, edge_types[i].end, edge_types[i].weight);
}
}
/* 查找连线顶点的尾部下标 */
int Find(int *parent, int f)
{
while ( parent[f] > 0)
{
f = parent[f];
}
return f;
}
/* 生成最小生成树 */
void MiniSpanTree_Kruskal(graph_type G)
{
int i, j, n, m;
int k = 0;
int parent[MAXVEX];/* 定义一数组用来判断边与边是否形成环路 */
edge_type edge_types[MAXedge_type];/* 定义边集数组,edge_type的结构为begin,end,weight,均为整型 */
/* 用来构建边集数组并排序 */
for ( i = 0; i < G.vertex_num-1; i++)
{
for (j = i + 1; j < G.vertex_num; j++)
{
if (G.arc[i][j]<INFINITY)
{
edge_types[k].begin = i;
edge_types[k].end = j;
edge_types[k].weight = G.arc[i][j];
k++;
}
}
}
sort(edge_types, &G);
for (i = 0; i < G.vertex_num; i++)
parent[i] = 0; /* 初始化数组值为0 */
for (i = 0; i < G.edge_type_num; i++) /* 遍历每一条边 */
{
n = Find(parent,edge_types[i].begin);
m = Find(parent,edge_types[i].end);
if (n != m) /* 假如n与m不等,说明此边没有与现有的生成树形成环路 */
{
parent[n] = m; /* 将此边的结尾顶点放入下标为起点的parent中。 */
/* 表示此顶点已经在生成树集合中 */
printf("(%d, %d) %d\n", edge_types[i].begin, edge_types[i].end, edge_types[i].weight);
}
}
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号