最短路径——Dijkstra算法与Floyd算法

最短路径问题
最短路径问题是我们经常会面临的一种决策问题。在图论中,非网图(边没有权值)的最短路径就是两个顶点之间经过边数最少的路径。对于网来说,由于每条边都有权值,所谓的最短路径是指,两个顶点之间经过的边加权之后的和最小。路径上的第一个顶点称为源点,最后一个顶点称为终点。求最短路径的经典算法有Dijkstra算法和Floyd算法。
Dijkstra算法
Dijkstra算法主要解决从某个源点到其余各个顶点的最短路径问题,它是一种按路径长度递增的次序来产生最短路径的算法。下面介绍算法思想。
首先给出一个6顶点的图,求v0到v5之间的最短路径
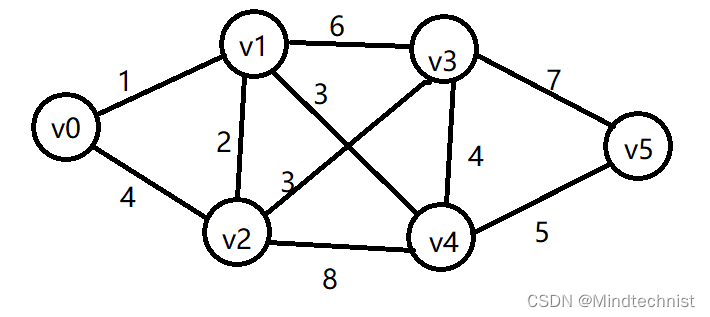
第一步,从v0开始到下一个顶点的权值最小边所对应的终点,从v0出发有两条边,v0v1和v0v2,权值更小的是v0v1;
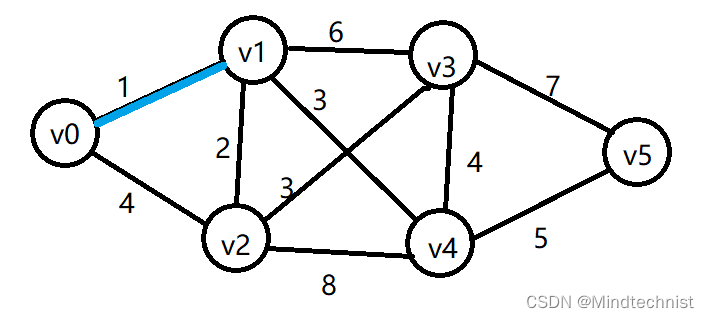
第二步,v1到下一个顶点的最小权值边,从三个待选项中选出权值最小的边;
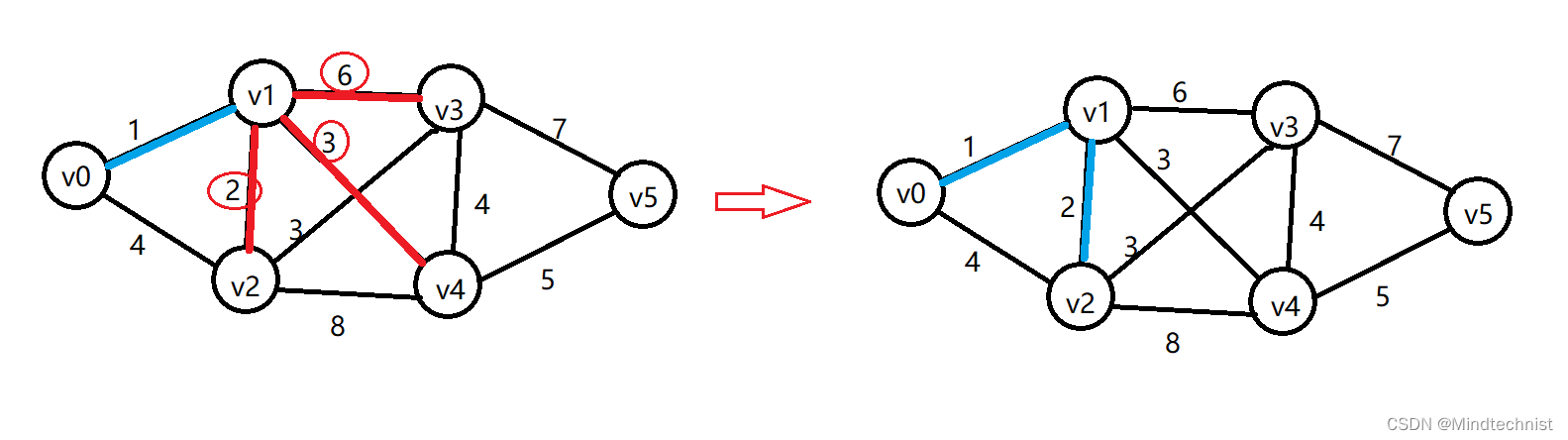
一直这样寻找下去,直到到达终点v5。
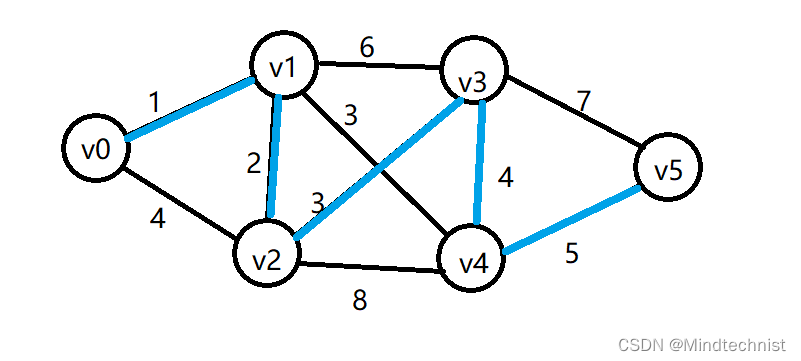
C语言代码实现
/* Dijkstra算法 */
#define MAXVEX 6
#define INFINITY 65535
typedef struct _graph_type
{
int vertex[MAXVEX]; /*顶点*/
int arc[MAXVEX][MAXVEX]; /*邻接矩阵*/
int vertex_num;
}graph_type;
typedef int pv_type[MAXVEX]; /* 用于存储最短路径下标的数组 */
typedef int plen_type[MAXVEX]; /* 用于存储到各点最短路径的权值和 */
/*
* graph : 图
* v0 :起始顶点
* path_vector :记录路径中vi顶点的上一个顶点的数组,[0, 0, 1]表示v2上一个顶点是v1,v1上一个顶点是v0
* 数组下标表示i,相应的值表示上一个顶点的下标 --- 实际上就是记录路径的
* path_length :v0到vi之间的路径和的数组
*/
void ShortestPath_Dijkstra(graph_type graph, int v0, pv_type *path_vector, plen_type *path_length)
{
int v;
int w;
int k; /*记录最小权值的边的顶点*/
int min; /*记录最小权值*/
int flag[MAXVEX];/* 标志是否找到最小路径,flag[w]=1表示求得顶点v0至vw的最短路径 */
for(v=0; v<graph.vertex_num; v++) /* 初始化数据 */
{
flag[v] = 0; /* 全部顶点初始化为未知最短路径状态 */
(*path_length)[v] = graph.arc[v0][v]; /* 根据邻接矩阵将与v0点有连线的顶点加上权值 */
(*path_vector)[v] = -1; /* 初始化路径数组P为-1 */
}
(*path_length)[v0] = 0; /* v0至v0路径为0 */
flag[v0] = 1; /* v0至v0不需要求路径 */
/* 开始主循环,每次求得v0到某个v顶点的最短路径 */
for(v=1; v<graph.vertex_num; v++)
{
min=INFINITY; /* min初始化为无穷大 */
for(w=0; w<graph.vertex_num; w++) /* 寻找离v0最近的顶点 */
{
if(!flag[w] && (*path_length)[w]<min) /* 遍历path_length数组,找到最小权值 */
{
k=w; /* 记录最小权值顶点 */
min = (*path_length)[w]; /* 更新min,w顶点离v0顶点更近 */
}
}
flag[k] = 1; /* 已找到,标志置1 */
for(w=0; w<graph.vertex_num; w++) /* 修正当前最短路径及距离 */
{
/* 如果经过v顶点的路径比现在这条路径的长度短的话 */
if(!flag[w] && (min+graph.arc[k][w]<(*path_length)[w]))
{ /* 说明找到了更短的路径,修改path_length[w]和path_vector[w] */
(*path_length)[w] = min + graph.arc[k][w]; /* 修改当前路径长度 */
(*path_vector)[w]=k; /*记录上一个顶点*/
}
}
}
}
代码解析
本代码略显复杂,有些晦涩难懂,下面讲解本代码的思路:
首先看代码中的注释,了解每个变量的用途,这里要关注三个数组path_vector、path_length和flag。在主循环之前都是声明和初始化的工作,下面从主循环开始讲解。
主循环第一次循环: 首先,主循环的作用是通过每一次循环得到源点v0到一个顶点的最短路径,v从1开始循环。
path_length数组用于保存路径和,第一次循环的时候为[0, 1, 4, 65535, 65535, 65535],第一个0表示v0和v0之间不需要计算路径,1表示v0到v1之间的权值为1,4表示v0到v3之间权值为4,后面的65535表示没有路径。

然后遍历path_length数组,找到最小的权值,记录下该权值以及对应的终点
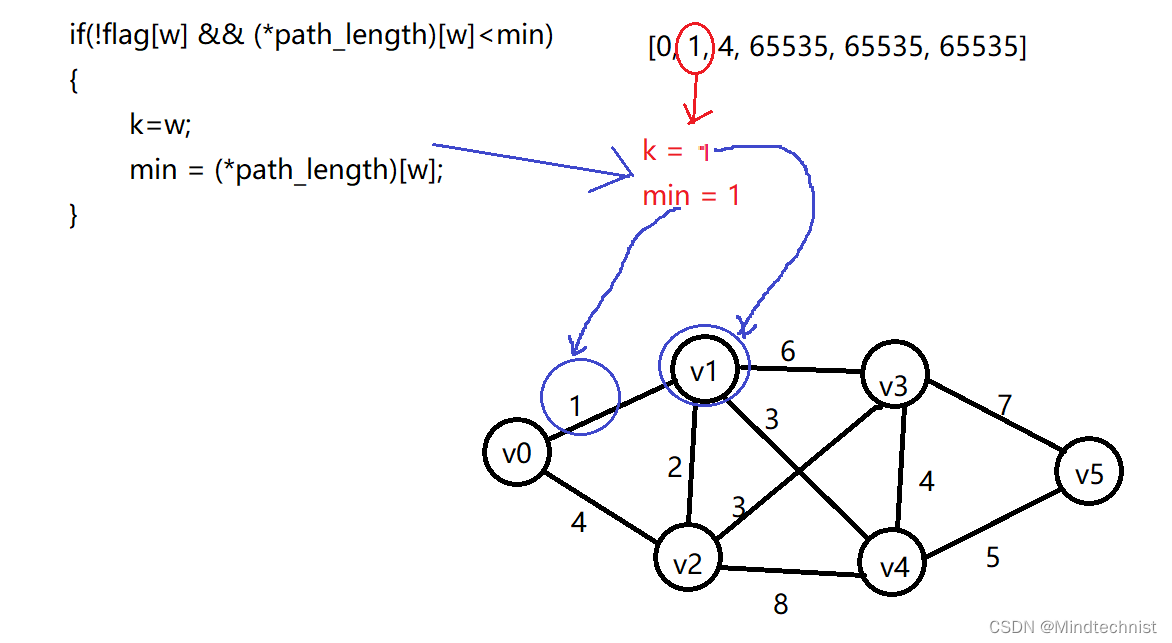
现在,v0到v1之间的路径找到了,那么更新flag为[1, 1, 0, 0, 0, 0],前两个1表示v0v0之间不需要找,v0v1之间的最短路径已找到。后面每找到v0到某一顶点的最短路径,就把flag数组中对应下标的数组元素值改为1。
修正最短路径: 这是最重要的一步,主要是为了修正path_length数组中的值。首先,经过前面的操作之后,该数组值当前是[0, 1, 4, 65535, 65535, 65535],也就是说v0到v1最短路径为1,这个毫无疑义,但是v0到v2最短路径是4,这个4是从邻接矩阵中直接拿过来的,并没有经过任何算法的检验,所以我们要修正这个值。
我们看图,从v0到v2目前有两条路,第一条v0v2,权值为4;第二条v0v1v2,权值为3。显然后者权值更小,我们应对数组path_length中的4进行修正。
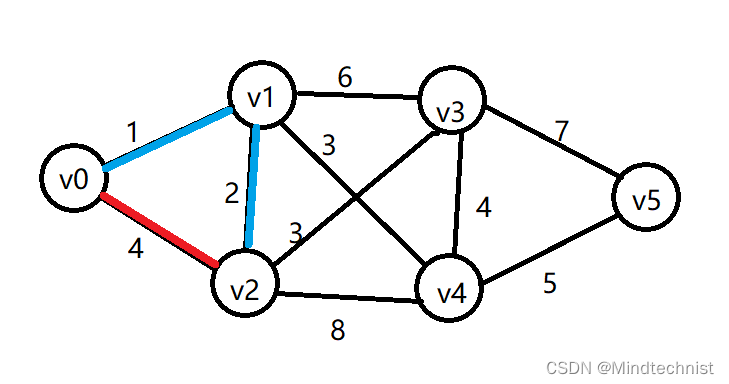
在修正最短路径的同时,我们应该把这条路径记录下来,也就是说v0是怎么到达v2的,是v0v2还是v0v1v2,这个路径是通过path_vector来记录的。

OK,第一轮循环结束,后面就是不断地重复这个过程,直到找出最短路径。在最后一次循环,我们得到的path_length和path_vector应该分别是:
path_length = [0, 1, 3, 6, 10, 15]
path_vector = [-1, 0, 1, 2, 3, 4]
[0, 1, 3, 6, 10, 15]表示,v0-v1之间最短路径是1,v0-v2之间最短路径是3,v0-v3之间最短路径是6,v0-v4最短路径是10,v0-v5最短路径是15。
[-1, 0, 1, 2, 3, 4]表示,v1的上一个顶点是0,v2的上一个顶点是v1,v3的上一个顶点是v2,v4的上一个顶点是v3,v5的上一个顶点是v4,这样就形成了一条路径v5 --> v4 --> v3 --> v2 --> v1 --> v0。
通过这两个数组我们可以看出,Dijkstra算法只能得到某一个顶点到其它任意顶点的最短路径,比如v0分别到v12345之间的最短路径,但是无法得到诸如v2到v4之间的最短路径,这就要看Floyd算法了。
Floyd算法
算法解析
依然是使用上面的图
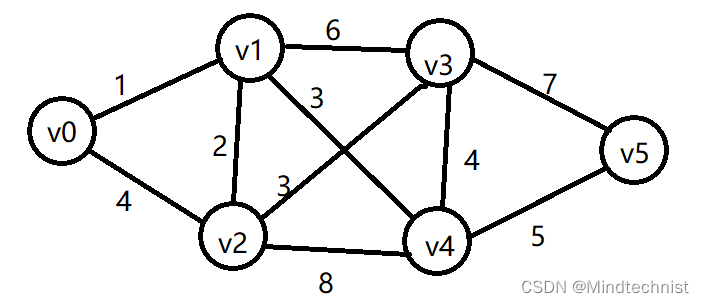
算法开始,首先初始化两个矩阵,path_length用于记录最短路径的长度,初始值为图的邻接矩阵;path_vector用来记录路径,也就是中转结点,可以结合程序来理解。
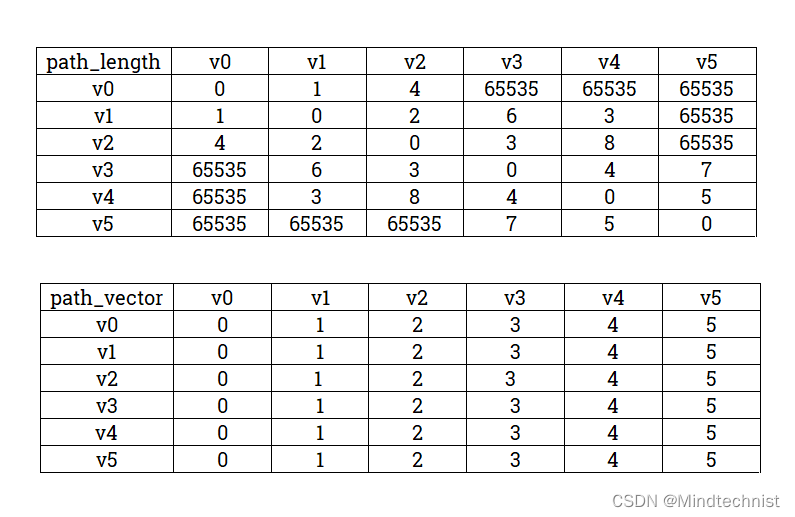
我们来看所有以v1为中转点的路径,也就是path_length矩阵的v1列,path_length,首先看图,经过v1中转可以到达v2、v3、v4,我们分别计算出v0 --> v1 --> v2,v0 --> v1 --> v3,v0 --> v1 --> v4的路径长度为3,7,4,然后分别和path_length矩阵中记录的v0 --> v2,v0 --> v3,v0 --> v4的最短路径值做对比,并更新path_length矩阵。
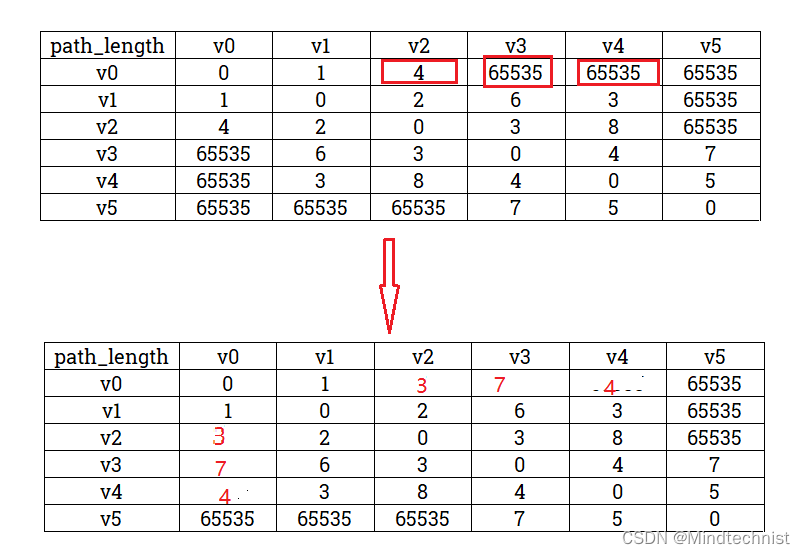
相应的,我们要修改路径矩阵中对应的位置,此时应该记录下来v2、v3、v4三个顶点的前驱顶点,它们分别是由v1顶点中转,此时将path_vector中v0 --> v2,v0 --> v3,v0 --> v4的中转结点记录为v1,表示在矩阵中就是path_vector[0][2]、path_vector[0][3]、path_vector[0][4]的值设置为1。
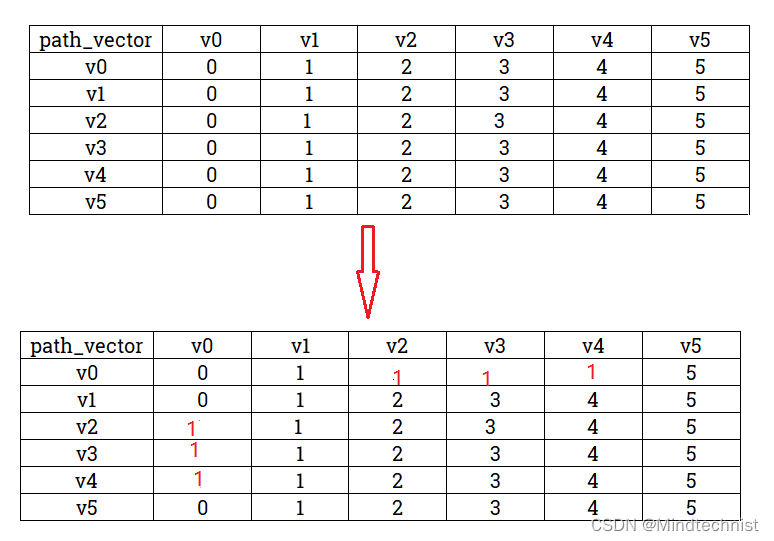
下面就是从以v2为中转点的路径开始重复上述过程,直到算法计算完以v4为中转顶点的路径,得到最终的path_length和path_vector矩阵。
C语言代码实现
/*Floyd算法*/
#define MAXVEX 6
#define INFINITY 65535
typedef struct _graph_type
{
int vertex[MAXVEX];
int arc[MAXVEX][MAXVEX];
int vertex_num;
}graph_type;
/*在Dijkstra算法中这两个都是一维数组,但是Floyd算法求的是任意顶点到其他顶点的最短路径,所以是二维数组*/
typedef int pv_type[MAXVEX][MAXVEX];
typedef int plen_type[MAXVEX][MAXVEX];
/* 求网图graph中各顶点v到其余顶点w的最短路径path_vector[v][w]及带权长度path_length[v][w]。 */
void ShortestPath_Floyd(graph_type graph, pv_type *path_vector, plen_type *path_length)
{
int v; /*起点*/
int w; /*终点*/
int k; /*中转点*/
for(v=0; v<graph.vertex_num; ++v) /* 初始化 */
{
for(w=0; w<graph.vertex_num; ++w)
{
(*path_length)[v][w]=graph.arc[v][w]; /* path_length初始化为邻接矩阵 */
(*path_vector)[v][w]=w; /* 初始化path_vector */
}
}
for(k=0; k<graph.vertex_num; ++k)
{
for(v=0; v<graph.vertex_num; ++v)
{
for(w=0; w<graph.vertex_num; ++w)
{
if ((*path_length)[v][w]>(*path_length)[v][k]+(*path_length)[k][w])
{/* 如果经过下标为k顶点路径比原两点间路径更短 */
(*path_length)[v][w]=(*path_length)[v][k]+(*path_length)[k][w];/* 将当前两点间权值设为更小的一个 */
(*path_vector)[v][w]=(*path_vector)[v][k];/* 路径设置为经过下标为k的顶点 */
}
}
}
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号