dp-双调欧几里德旅行商问题
双调欧几里德旅行商问题
算法导论3rd - 15.3
问题描述
平面上n个点,确定一条连接各点的最短闭合旅程。这个解的一般形式为NP的(在多项式时间内可以求出)
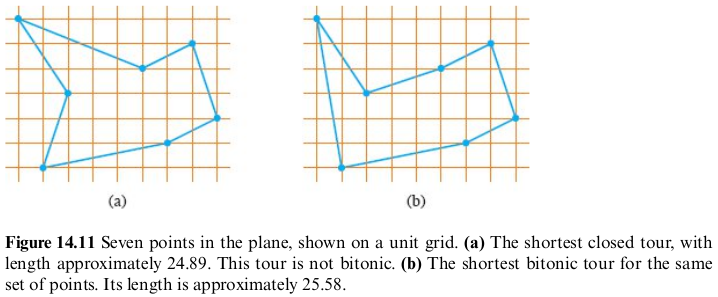
J.L. Bentley 建议通过只考虑双调旅程(bitonictour)来简化问题,这种旅程即为从最左点开始,严格地从左到右直至最右点,然后严格地从右到左直至出发点。在这种情况下,多项式的算法是可能的。事实上,存在确定的最优双调路线的O(n*n)时间的算法。
下图(b)显示了同样的7个点的最短双调路线。
分析
将节点按x方向排序,从最左端开始出发,分为两条路径,严格从左到右依次经过不重复的点,且不能跳过节点,到达最右侧节点。
用cost[i][j]表示两条路径分别到达i,j点的最小距离代价。即两条路径 <0...i>和<0...j> 的总代价。
如果<0...i...N>和<0...j...N>是两条最短路径,那么<0...i>和<0...j>也是最短路径,由此,问题可以进行分解。
假设共有7个节点,从左往右依次标为0...6。
代价表格cost[i][j]假设i>j。(cost[i][j]与cost[j][i]相等)
如果将问题理解为依次将0...6号节点往两条路径中添加,则计算i节点的代价时,0...i-1号节点已经添加到两条路径中了,不能跳过节点。即计算cost[i][0...i-1]时cost[i-1][0...i-2]已经计算完成。
两条路径到达6号节点的前一步是其中一条路径已经到达了5,可能的路径有:cost[5][0],cost[5][1],cost[5][2],cost[5][3],cost[5][4].
cost[5][0]表示一条路经经过了012345,而另一条路径还没出发;
cost[5][1]表示一条路经经过了02345,另一条路径为01;
cost[5][2]则可能有两种情况:01345|02 和 0345|012,选择距离代价最小者;
cost[5][3]则有4种情况;
cost[5][4]有8种情况,不一一列举;
如法炮制,可以分析cost[5][0...4],然后再推导cost[4][0...3],依次类推,直到cost[0][0]
递推关系
cost[6][6] = min(
cost[5][0] + dist[5,6] + dist[0,6],
cost[5][1] + dist[5,6] + dist[1,6],
cost[5][2] + dist[5,6] + dist[2,6],
cost[5][3] + dist[5,6] + dist[3,6],
cost[5][4] + dist[5,6] + dist[4,6],
)
cost[5][4] = min(
cost[0][4] + dist[0][5],
cost[1][4] + dist[1][5],
cost[2][4] + dist[2][5],
cost[3][4] + dist[3][5],
)
// 因为不允许跳过,所以当 i!=j+1 时,只有一种情况到达当前节点,以下几种情况皆是,后同
cost[5][3] = cost[4][3] + dist[4][5]
cost[5][2] = cost[4][2] + dist[4][5]
cost[5][1] = cost[4][1] + dist[4][5]
cost[5][0] = cost[4][0] + dist[4][5]
cost[4][3] = min(
cost[0][3] + dist[0][4],
cost[1][3] + dist[1][4],
cost[2][3] + dist[2][4],
)
cost[4][2] = cost[3][2] + dist[3][4]
cost[4][1] = cost[3][1] + dist[3][4]
cost[4][0] = cost[3][0] + dist[3][4]
cost[3][2] = min(
cost[0][2] + dist[0][3],
cost[1][2] + dist[1][3],
)
cost[3][1] = cost[2][1] + dist[2][3]
cost[3][0] = cost[2][0] + dist[2][3]
cost[2][1] = cost[0][1] + dist[0][2]
cost[2][0] = cost[1][0] + dist[1][2]
cost[1][0] = cost[0][0] + dist[0][1]
cost[0][0] = 0
在计算时,将代价最小的路径记录下来。
程序
// 双调欧几里德旅行商问题
#include <iostream>
#include <new>
#include <time.h>
#include <float.h>
#include <vector>
#include <string.h>
#include <math.h>
using namespace std;
struct Node {
int x;
int y;
};
void solve();
template<typename T>
void print_mat(T** mat, int len1, int len2);
int main(int argc, char** argv) {
clock_t start, end;
start = clock();
solve();
end = clock();
cout << "time cost: " << (end-start)*1000./CLOCKS_PER_SEC << " ms\n";
return 0;
}
void solve() {
vector<Node> nodes{
{1,1},
{2,7},
{3,4},
{6,3},
{7,6},
{8,2},
{9,5},
};
// dist是各点间距离,只使用右上
double** dist = new double*[nodes.size()];
// cost左下是距离代价,右上记录当前路径的上一步的路径(节点)
double** cost = new double*[nodes.size()];
for (int i = 0; i < nodes.size(); ++i) {
dist[i] = new double[nodes.size()]{0};
cost[i] = new double[nodes.size()]{0};
}
for (int i = 0; i < nodes.size(); ++i) {
for (int j = 0; j < i; ++j) {
dist[j][i] = sqrt(double((nodes[i].x-nodes[j].x)*(nodes[i].x-nodes[j].x)
+ (nodes[i].y-nodes[j].y)*(nodes[i].y-nodes[j].y)));
}
}
cost[0][0] = 0;
cost[1][0] = dist[0][1];
for (int i = 2; i < nodes.size() - 1; ++i) {
for (int j = 0; j < i; ++j) {
if (j == i-1) {
cost[i][j] = DBL_MAX;
double c;
for (int k = 0; k < j; ++k) {
c = cost[j][k] + dist[k][i];
if (c < cost[i][j]) {
cost[i][j] = c;
cost[j][i] = k;
}
}
} else {
cost[i][j] = cost[i-1][j] + dist[i-1][i];
cost[j][i] = i;
}
}
}
// 最右侧点路径计算(N为点的个数,下标从0开始)
// cost[N-1][N-1] = cost[N-2][k] + dist[N-2][N-1] + dist[k][N-1] (N=nodes.size())
// 与最右侧点相连的点其中一个是倒数第二个点,即nodes[N-2],另一个点设为n,此处确定n的值
int n = -1;
cost[nodes.size()-1][nodes.size()-1] = DBL_MAX;
for (int k = 0; k < nodes.size() - 2; ++k) {
double c = cost[nodes.size()-2][k] + dist[nodes.size()-2][nodes.size()-1]
+ dist[k][nodes.size()-1];
if (c < cost[nodes.size()-1][nodes.size()-1]) {
cost[nodes.size()-1][nodes.size()-1] = c;
n = k;
}
}
cout << "cost: \n";
print_mat(cost, nodes.size(), nodes.size());
cout << "dist: \n";
print_mat(dist, nodes.size(), nodes.size());
cout << n << endl; // 倒数第二步的路径(节点)
// 输出路径
int i = nodes.size() - 2, j = n, k;
cout << i << " -> " << nodes.size() - 1 << endl;
cout << j << " -> " << nodes.size() - 1 << endl;
while (i) {
k = cost[j][i];
if (k == i) {
--i;
cout << i << " -> " << k << endl;
} else {
cout << k << " -> " << i << endl;
i = j;
j = k;
}
}
for (int i = 0; i < nodes.size(); ++i) {
delete[] dist[i];
delete[] cost[i];
}
delete[] dist;
delete[] cost;
}
template<typename T>
void print_mat(T** mat, int len1, int len2) {
for (int i = 0; i < len1; ++i) {
for (int j = 0; j < len2; ++j) {
cout << mat[i][j] << "\t";
}
cout << endl;
}
}
测试:
cost:
0 0 2 3 4 5 0
6.08276 0 0 3 4 5 0
9.24504 9.68831 0 0 4 5 0
12.4073 12.8506 14.6302 0 1 5 0
15.5696 16.0129 17.7925 17.9496 0 3 0
19.6927 20.136 21.9156 22.0727 20.1857 0 0
0 0 0 0 0 0 25.584
dist:
0 6.08276 3.60555 5.38516 7.81025 7.07107 8.94427
0 0 3.16228 5.65685 5.09902 7.81025 7.28011
0 0 0 3.16228 4.47214 5.38516 6.08276
0 0 0 0 3.16228 2.23607 3.60555
0 0 0 0 0 4.12311 2.23607
0 0 0 0 0 0 3.16228
0 0 0 0 0 0 0
4
5 -> 6
4 -> 6
3 -> 5
1 -> 4
2 -> 3
0 -> 2
0 -> 1
time cost: 0.114 ms


 浙公网安备 33010602011771号
浙公网安备 33010602011771号