dp-最优二叉搜索树
最优二叉搜索树
问题描述
最优二叉搜索树(Optimal Binary Search Tree,Optimal BST)问题,形式化定义:给定一个n个不同关键字的已排序的序列K=<k1, k2, ..., kn>(k1<k2<...<kn),用这些关键字构造一棵二叉搜索树 —— 对每个关键字ki,都有一个概率pi表示其搜索频率。对于不在K中的搜索值构造n+1个”伪关键字“d0, d1, d2, ..., dn —— 伪关键字di表示所有在ki和ki+1之间的值(i=1,2,...,n-1,d0表示所有小于k1的值,dn表示所有大于kn的值),每个伪关键字di对应一个概率qi(搜索频率)。
例如,对一个n=5的关键字集合及如下的搜索频率,构造二叉搜索树。
| i | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| pi | 0 | 0.15 | 0.1 | 0.05 | 0.1 | 0.2 |
| qi | 0.05 | 0.1 | 0.05 | 0.05 | 0.05 | 0.1 |
如下为两种可能的结构,左侧的期望代价为2.8,右侧为最优2.75
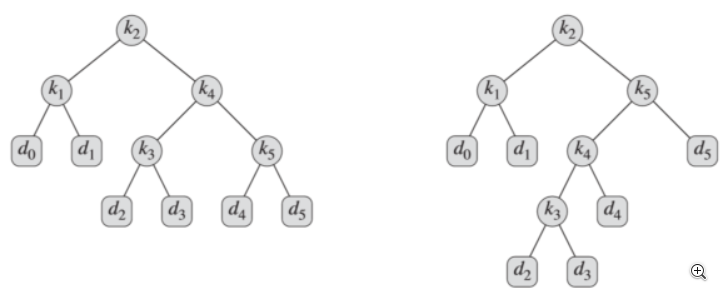
另外,上述例子有两种最优,期望代价均为2.75,另一种是:(并且它的深度更小)
k4
k2 k5
k1 k3 d4 d5
d0 d1 d2 d3
问题分析
分析这个问题,要从观察子树特征开始。一个二叉搜索树的任意子树,必须包含连续关键字 ki...kj 和伪关键字 di-1...dj.
而每个子树都有且只有一个根节点,根节点k将子树分为两部分: <i...k-1> 和 <k+1...j>,分别为左右子树。
所以问题转化为了递归地求解连续节点的根节点问题,假设函数f为期望代价:
f(i...j) = min(
f(i-1)+f(i+1...n)+c[i...j], // i为根节点
f(i)+f(i+2...n)+c[i...j], // i+1为根节点
f(i..i+1)+f(i+3...n)+c[i...j], // i+2为根节点
...
f(i..k-1)+f(k+1...n)+c[i...j], // k为根节点
...
f(i...j-1)+f(j+1)+c[i...j] // j为根节点
)
对某种已知结构的二叉树,每个节点的搜索代价为其搜索概率乘以深度+1(根节点深度为0,所以加1),然后将树中所有节点代价相加,得到树的期望搜索代价。
当将两个子树放在其同一个根节点上组成一个新的树时,所有节点深度都增加1,所以上述递推关系中,每种情况都增加了一个额外的代价c[i...j],即ki到kj所有节点的搜索概率之和:
c[i...j] = sum(ki...kj) + sum(di-1...dj)
思路
e[i,j] 为<i...j>构成的子树最小期望代价
w[i,j] 为<i...j>构成的子树所有节点概率相加,相当于上面的c[i...j]
root[i,j] 为<i...j>构成的子树最小期望对应的根节点id
为了处理边界问题,e和w长度都增加1,即第一维长度为n+1
OPTIMAL-BST(p, q, n)
let e[1 : n + 1, 0 : n], w[1 : n + 1, 0 : n], and root[1 : n, 1 : n] be new tables
for i = 1 to n + 1
e[i, i - 1] = q_{i-1}
w[i, i - 1] = q_{i-1}
for l = 1 to n
for i = 1 to n - l + 1
j = i + l - 1
e[i, j] = ∞
w[i, j] = w[i, j - 1] + p_j + q_j
for r = i to j
t = e[i, r - 1] + e[r + 1, j] + w[i, j]
if t < e[i, j]
e[i, j] = t
root[i, j] = r
return e and root
程序
// optimal binary search tree
// 最优二叉搜索树
#include <iostream>
#include <float.h>
#include <vector>
#include <climits>
#include <time.h>
#define N 7
using namespace std;
void solve();
template<typename T>
void print_mat(T** mat, int len1, int len2);
int main(int argc, char** argv) {
solve();
return 0;
}
void solve() {
//int keys[N+1]{0,1,2,3,4,5};
// 下标0的元素为0,是为了和weights2对齐,无意义
//double weights1[N+1]{0,0.15,0.1,0.05,0.1,0.2};
//double weights2[N+1]{0.05,0.1,0.05,0.05,0.05,0.1};
int keys[N+1]{0,1,2,3,4,5,6,7};
double weights1[N+1]{0,0.04,0.06,0.08,0.02,0.1,0.12,0.14};
double weights2[N+1]{0.06,0.06,0.06,0.06,0.05,0.05,0.05,0.05};
// 存放权重(期望),只有右上和对角下一行有值
// 对角下一行wei[i][i-1]表示weights2[i-1]
double** wei = new double*[N+1];
// wei1[i][j] : sum(weights1[i...j]) + sum(weights2[i-1,...,j])
double** wei1 = new double*[N+1];
// 右上角和对角存放根节点id,左下代表深度
int** rid = new int*[N+1];
for (int i = 0; i < N+1; ++i) {
wei[i] = new double[N+1]{0};
wei1[i] = new double[N+1]{0};
rid[i] = new int[N+1]{0};
if (i > 0) {
wei[i][i-1] = weights2[i-1];
wei[i][i] = weights1[i] + 2*(weights2[i-1] + weights2[i]);
rid[i][i] = i;
wei1[i][i-1] = weights2[i-1];
wei1[i][i] = weights1[i] + weights2[i-1] + weights2[i];
}
// 相邻两个节点组成的树深度为2(包括伪关键字,根节点深度为0)
// 剩余位置用一个比较大的值占位
for (int j = 0; j < i; ++j) {
rid[i][j] = i==j+1 ? 2 : N*2;
}
}
for (int diff = 1; diff < N; ++diff) {
for (int i = 1; i < N+1-diff; ++i) {
int j = i + diff;
wei1[i][j] = wei1[i][j-1] + weights1[j] + weights2[j];
wei[i][j] = DBL_MAX;
for (int k = i; k <= j; ++k) { // 旧方案
// 习题15.5-4, rid[i][j-1] <= rid[i][j] <= rid[i+1][j]
// 上一层循环的时间复杂度变为 O(n),总时间复杂度变为 O(n^2)
// 这样虽然时间复杂度降低了,但深度的计算变得不准确;旧方案的深度是准确的
// for (int k = rid[i][j-1]; k <= rid[i+1][j]; ++k) {
double w = wei1[i][j] + wei[i][k-1] + (k<N ? wei[k+1][j] : weights2[j]);
int deep = rid[j][i];
if (j == i+1) {
deep = 2;
} else {
if (k <= i+1) {
deep = rid[k+1][i] + 1;
} else if (j <= k+1) {
deep = rid[j][k-1] + 1;
} else {
deep = max(rid[k-1][i], rid[j][k+1]) + 1;
}
}
if (w <= wei[i][j]) {
wei[i][j] = w;
rid[i][j] = k;
if (deep < rid[j][i]) {
rid[j][i] = deep;
rid[i][j] = k;
}
}
cout << i << "," << j << "," << k << "\tw: " << w << "\td: " << deep << endl;
}
}
}
cout << "wei:\n";
print_mat(wei, N+1, N+1);
cout << "wei1:\n";
print_mat(wei1, N+1, N+1);
cout << "rid:\n";
print_mat(rid, N+1, N+1);
// print structure
cout << "structure:\n";
vector<pair<int, int>> stru{{1, N}};
pair<int, int> p;
int id, count = 1;
while (!stru.empty()) {
p = stru[0];
id = rid[p.first][p.second];
cout << keys[id];
if (p.first < id) {
stru.push_back({p.first, id-1});
} else {
cout << "(L)"; // 左子树为空
}
if (id < p.second) {
stru.push_back({id+1, p.second});
} else {
cout << "(R)"; // 右子树为空
}
stru.erase(stru.begin());
cout << "\t";
if (--count == 0) {
cout << endl;
count = stru.size();
}
}
for (int i = 0; i < N+1; ++i) {
delete[] wei[i];
delete[] wei1[i];
delete[] rid[i];
}
delete[] wei;
delete[] wei1;
delete[] rid;
}
template<typename T>
void print_mat(T** mat, int len1, int len2) {
for (int i = 0; i < len1; ++i) {
for (int j = 0; j < len2; ++j) {
cout << mat[i][j] << "\t";
}
cout << endl;
}
}
测试:
$ g++ -o bst bst.cpp && ./bst
1,2,1 w: 0.64 d: 2
1,2,2 w: 0.62 d: 2
2,3,2 w: 0.7 d: 2
2,3,3 w: 0.68 d: 2
3,4,3 w: 0.57 d: 2
3,4,4 w: 0.64 d: 2
4,5,4 w: 0.64 d: 2
4,5,5 w: 0.57 d: 2
5,6,5 w: 0.74 d: 2
5,6,6 w: 0.72 d: 2
6,7,6 w: 0.8 d: 2
6,7,7 w: 0.78 d: 2
1,3,1 w: 1.16 d: 3
1,3,2 w: 1.02 d: 4
1,3,3 w: 1.1 d: 3
2,4,2 w: 1.02 d: 3
2,4,3 w: 0.93 d: 4
2,4,4 w: 1.12 d: 3
3,5,3 w: 1.05 d: 3
3,5,4 w: 1.04 d: 4
3,5,5 w: 1.04 d: 3
4,6,4 w: 1.23 d: 3
4,6,5 w: 1.01 d: 4
4,6,6 w: 1.07 d: 3
5,7,5 w: 1.39 d: 3
5,7,6 w: 1.2 d: 4
5,7,7 w: 1.33 d: 3
1,4,1 w: 1.48 d: 3
1,4,2 w: 1.34 d: 4
1,4,3 w: 1.35 d: 4
1,4,4 w: 1.56 d: 3
2,5,2 w: 1.64 d: 3
2,5,3 w: 1.41 d: 4
2,5,4 w: 1.52 d: 4
2,5,5 w: 1.52 d: 3
3,6,3 w: 1.66 d: 3
3,6,4 w: 1.63 d: 4
3,6,5 w: 1.48 d: 4
3,6,6 w: 1.68 d: 3
4,7,4 w: 1.9 d: 3
4,7,5 w: 1.66 d: 4
4,7,6 w: 1.55 d: 4
4,7,7 w: 1.7 d: 3
1,5,1 w: 2.11 d: 3
1,5,2 w: 1.96 d: 4
1,5,3 w: 1.83 d: 3
1,5,4 w: 1.96 d: 4
1,5,5 w: 2.03 d: 3
2,6,2 w: 2.25 d: 3
2,6,3 w: 2.02 d: 4
2,6,4 w: 2.11 d: 3
2,6,5 w: 1.96 d: 4
2,6,6 w: 2.17 d: 3
3,7,3 w: 2.39 d: 3
3,7,4 w: 2.3 d: 4
3,7,5 w: 2.13 d: 3
3,7,6 w: 2.16 d: 4
3,7,7 w: 2.31 d: 3
1,6,1 w: 2.83 d: 3
1,6,2 w: 2.57 d: 4
1,6,3 w: 2.44 d: 4
1,6,4 w: 2.55 d: 4
1,6,5 w: 2.47 d: 4
1,6,6 w: 2.69 d: 3
2,7,2 w: 3.09 d: 3
2,7,3 w: 2.75 d: 4
2,7,4 w: 2.78 d: 4
2,7,5 w: 2.61 d: 4
2,7,6 w: 2.65 d: 4
2,7,7 w: 2.91 d: 3
1,7,1 w: 3.67 d: 3
1,7,2 w: 3.41 d: 4
1,7,3 w: 3.17 d: 4
1,7,4 w: 3.22 d: 4
1,7,5 w: 3.12 d: 4
1,7,6 w: 3.17 d: 4
1,7,7 w: 3.49 d: 3
wei:
0 0 0 0 0 0 0 0
0.06 0.28 0.62 1.02 1.34 1.83 2.44 3.12
0 0.06 0.3 0.68 0.93 1.41 1.96 2.61
0 0 0.06 0.32 0.57 1.04 1.48 2.13
0 0 0 0.06 0.24 0.57 1.01 1.55
0 0 0 0 0.05 0.3 0.72 1.2
0 0 0 0 0 0.05 0.32 0.78
0 0 0 0 0 0 0.05 0.34
wei1:
0 0 0 0 0 0 0 0
0.06 0.16 0.28 0.42 0.49 0.64 0.81 1
0 0.06 0.18 0.32 0.39 0.54 0.71 0.9
0 0 0.06 0.2 0.27 0.42 0.59 0.78
0 0 0 0.06 0.13 0.28 0.45 0.64
0 0 0 0 0.05 0.2 0.37 0.56
0 0 0 0 0 0.05 0.22 0.41
0 0 0 0 0 0 0.05 0.24
rid:
0 0 0 0 0 0 0 0
2 1 2 2 2 3 3 5
14 2 2 3 3 3 5 5
14 3 2 3 3 5 5 5
14 3 3 2 4 5 5 6
14 3 3 3 2 5 6 6
14 3 3 3 3 2 6 7
14 3 3 3 3 3 2 7
structure:
5
2 7(R)
1(L)(R) 3(L) 6(L)(R)
4(L)(R)
time cost: 0.32 ms
新方案的时间是 0.255 ms,但深度计算错误


 浙公网安备 33010602011771号
浙公网安备 33010602011771号