二分-小车问题

小车问题

目录

• 小车问题
  • 题目描述
  • 分析
  • 程序

题目描述

・甲、乙两人同时从A地出发要尽快同时赶到B地。出发时A地有一辆小车，可是这辆小车除了驾驶员外只能带一人。 已知甲、乙两人的步行速度一样，且小于车的速度。问：怎样利用小车才能使两人尽快同时到达。

・输入
・仅一行，三个数据分别表示人AB两地的距离s，人的步行速度a，车的速度b

・输出
・两人同时到达3地需要的最短时间（保留四位小数）

・样例输入
・120 5 25

・样例输出
・9.6000

分析

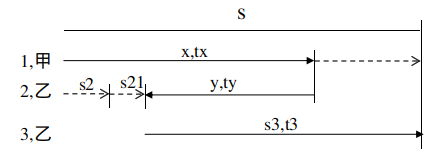
・假设，小车先带甲出发前往B地，乙步行，当前进到距离A地x时，甲下车步行到B地，小车回来接乙,设甲到达时间为t1，乙到达时间为t2.

问题转换为了求合适的x，使得t1和t2相等

・设方程:
\(f(x) = t1 - t2\)
当x增加时t1会减小,t2增大，所以此函数为减函数,并且f(0)>0,f(s)<0,因此在[0,s]上方程f(x)=0有唯一实根。
对于单调函数，用二分法求解。

vc为车的速度，vm为人的速度，则：
\(t1 = x/v_c + (s-x)/v_m\)
\(t2 = x/v_c + 相遇的时间(s21/v_m) + 坐车时间(s3/vc)\)
经计算：
\(相遇时间 = x*(v_c-v_m)/((v_c+v_m)*v_c)\)
\(坐车时间 = s/v_c - x*2*v_m/((v_c+v_m)*v_c)\)

程序

#include <iostream>
#include <time.h>

using namespace std;

void solve();

int main(int argc, char** argv) {
    clock_t start, end;
    start = clock();
    solve();
    end = clock();
    cout << "time cost: " << (end-start)*1000./CLOCKS_PER_SEC << " ms\n";

    return 0;
}

// vm 是人的速度，vc是车的速度
void solve() {
    double s = 120., vm = 5., vc = 25.;
    double l = 0., r = s, x = 0.;
    double t1, t2;
    while (r-l > 10e-5) {
        x = (r + l) / 2.;       // 二分法求解
        t1 = x / vc + (s - x) / vm;
        t2 = 2 * x * (vc-vm) / ((vc + vm) * vc) + s / vc;
        //cout << "x: " << x << ", t1: " << t1 << ", t2: " << t2 << endl;
        if (t1 < t2) {
            r = x;
        } else {
            l = x;
        }
    }
    cout << "x: " << x << ", t1: " << t1 << endl;
}

测试：

$ g++ -o vehicle vehicle.cpp && ./vehicle
x: 90, t1: 9.6
time cost: 0.033 ms