ALGO-27_蓝桥杯_算法训练_FBI树(树，递归)

问题描述
　　我们可以把由“0”和“1”组成的字符串分为三类：全“0”串称为B串，全“1”串称为I串，既含“0”又含“1”的串则称为F串。
　　FBI树是一种二叉树，它的结点类型也包括F结点，B结点和I结点三种。由一个长度为2N的“01”串S可以构造出一棵FBI树T，递归的构造方法如下：
　　1)T的根结点为R，其类型与串S的类型相同；
　　2)若串S的长度大于1，将串S从中间分开，分为等长的左右子串S1和S2；由左子串S1构造R的左子树T1，由右子串S2构造R的右子树T2。
　　现在给定一个长度为2N的“01”串，请用上述构造方法构造出一棵FBI树，并输出它的后序遍历序列。
输入格式
　　第一行是一个整数N（0 <= N <= 10），第二行是一个长度为2N的“01”串。
输出格式
　　包括一行，这一行只包含一个字符串，即FBI树的后序遍历序列。
样例输入
3
10001011
样例输出
IBFBBBFIBFIIIFF
数据规模和约定
　　对于40%的数据，N <= 2；
　　对于全部的数据，N <= 10。
　　注：
　　[1] 二叉树：二叉树是结点的有限集合，这个集合或为空集，或由一个根结点和两棵不相交的二叉树组成。这两棵不相交的二叉树分别称为这个根结点的左子树和右子树。
　　[2] 后序遍历：后序遍历是深度优先遍历二叉树的一种方法，它的递归定义是：先后序遍历左子树，再后序遍历右子树，最后访问根。

 

记:

一开始解题根据惯用FBI树解法：建树->递归判断数据并记录->后序输出树

　　　　　　　　

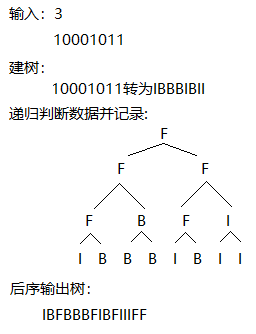
这种解法在输入n较大时会出现超时现象，

明显在建树以及后序输出遍历输出树的过程浪费了很多时间；

 

本题中的数据采用二叉树存储，而且是后序遍历输出树，

所以我们可以采用类似二分查找的形式，

先对输入数据进行二分区，然后进行判断

输出判断后的字符('F','B','I')，并返回

从而节省了建树以后序遍历输出树的时间。

 

AC代码:

#include <stdio.h> 
#define MAX (1<<10)

int n = 0 ;
char str[MAX+1] = {0};

void init()
{
    int i,j;
    scanf("%d",&n);
    for (i = 1 ; i <= (1<<n) ; i ++)
    {
        scanf("%1d",&j);
        /*将输入的数字串转换为FBI串*/ 
        if (j)
        {
            str[i] = 'I';
        }
        else
        {
            str[i] = 'B';
        }
    }    
    return ;    
}

char check(char l,char r)
{
    if (l == 'B' && r == 'B')
    {
        return 'B';
    }
    else if (l == 'I' && r == 'I')
    {
        return 'I';
    }
    else
    {
        return 'F';
    }
}

char fbi(int x,int y)
{
    int i = x , j = y , k = (y-x)/2;
    char l,r,ans = str[i];
    if (i < j)
    {
        /*递归分区间*/ 
        l = fbi(i,i+k);/*左子树*/ 
        r = fbi(j-k,j);/*右子树*/ 
        ans = check(l,r);
    }
    printf("%c",ans);
    return ans;
}

int main(void)
{
    init();    
    fbi(1,1<<n);
    return 0;
}