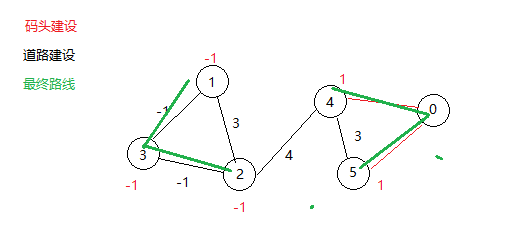
问题描述 栋栋居住在一个繁华的C市中,然而,这个城市的道路大都年久失修。市长准备重新修一些路以方便市民,于是找到了栋栋,希望栋栋能帮助他。 C市中有n个比较重要的地点,市长希望这些地点重点被考虑。现在可以修一些道路来连接其中的一些地点,每条道路可以连接其中的两个地点。另外由于C市有一条河从中穿过,也可以在其中的一些地点建设码头,所有建了码头的地点可以通过河道连接。 栋栋拿到了允许建设的道路的信息,包括每条可以建设的道路的花费,以及哪些地点可以建设码头和建设码头的花费。 市长希望栋栋给出一个方案,使得任意两个地点能只通过新修的路或者河道互达,同时花费尽量小。 输入格式 输入的第一行包含两个整数n, m,分别表示C市中重要地点的个数和可以建设的道路条数。所有地点从1到n依次编号。 接下来m行,每行三个整数a, b, c,表示可以建设一条从地点a到地点b的道路,花费为c。若c为正,表示建设是花钱的,如果c为负,则表示建设了道路后还可以赚钱(比如建设收费道路)。 接下来一行,包含n个整数w_1, w_2, …, w_n。如果w_i为正数,则表示在地点i建设码头的花费,如果w_i为-1,则表示地点i无法建设码头。 输入保证至少存在一个方法使得任意两个地点能只通过新修的路或者河道互达。 输出格式 输出一行,包含一个整数,表示使得所有地点通过新修道路或者码头连接的最小花费。如果满足条件的情况下还能赚钱,那么你应该输出一个负数。 样例输入 5 5 1 2 4 1 3 -1 2 3 3 2 4 5 4 5 10 -1 10 10 1 1 样例输出 9 样例说明 建设第2、3、4条道路,在地点4、5建设码头,总的花费为9。 数据规模和约定 对于20%的数据,1<=n<=10,1<=m<=20,0<=c<=20,w_i<=20; 对于50%的数据,1<=n<=100,1<=m<=1000,-50<=c<=50,w_i<=50; 对于70%的数据,1<=n<=1000; 对于100%的数据,1 <= n <= 10000,1 <= m <= 100000,-1000<=c<=1000,-1<=w_i<=1000,w_i≠0。
代码如下:

1 #include <bits/stdc++.h> 2 #include <algorithm> 3 using namespace std; 4 #define N 200010 5 #define INF 0xfffffff 6 7 typedef struct node 8 { 9 int x;//起点 10 int y;//终点 11 int v;//费用 12 }node; 13 14 int n,m; //地点数,可建道路数 15 int f[N]; //并查集 16 node e[N]; 17 18 int cmp(node a,node b) 19 { 20 return a.v<b.v;//按照费用从小到大排序 21 } 22 23 int find(int x)//寻找线段根 24 { 25 return x==f[x]?x:(f[x]=find(f[x])); 26 } 27 28 int kruskal() 29 { 30 int num,ans; 31 sort(e,e+m,cmp);//按照费用从小到大排序 32 for (int i=0 ; i<=n ; i++) 33 f[i] = i;//初始化并查集 34 35 num = ans = 0; 36 for (int i=0 ; i<m ; i++) 37 { 38 int tx = find(e[i].x);//寻找x对应的树根 39 int ty = find(e[i].y);//寻找y对应的树根 40 if (tx!=ty || e[i].v<0)//两地点不连接 ,或者本次建设可赚钱 41 { 42 f[tx] = ty; //更新并查集 43 ans += e[i].v; //更新最小边权和 44 num ++; 45 } 46 } 47 if (num < n-1)//本次搜索无法并联所有地点 48 return INF; 49 return ans; 50 } 51 52 int main(void) 53 { 54 int i,ans; 55 scanf("%d%d",&n,&m); 56 for (i=0 ; i<m ; i++)//遍历建设道路费用 57 { 58 scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].v); 59 } 60 ans = kruskal();//得到无码头时的最小边权和 61 for (i=1 ; i<=n ; i++)//遍历建设码头费用 62 { 63 scanf("%d",&e[m].v); 64 if (e[m].v != -1)//该地点可建设码头 65 { 66 e[m].x = 0; 67 e[m].y = i; 68 m ++; 69 } 70 } 71 n++; 72 ans = min(ans,kruskal());//比较得到[ 无码头建设 ]与[ 有码头建设 ]的最小边权和 73 printf("%d",ans); 74 75 return 0; 76 }
解题思路:
利用Kruskal算法,可以获得其对应的最小生成树,其边权值和即为题目对应的最小费用;
1.第一次使用Kruskal算法,对应无建设码头,生成的为只建设道路的最小费用;
2.第二次使用Kruskal算法,对应有建设码头(码头默认连接到 0 ,无对应的地点),生成的为建设道路与码头的最小费用;
(在第二次计算中,由于码头的建设,可能会出现区域独立,即一部分区域道路连接,一部分水路连接,两区域无交集,结果需抛弃)