从统计看机器学习(二) 多重共线性的一些思考

　　从一个生活中的现象说起：我们在装机时，不会安装一款以上的解压软件，也不希望被莫名其妙地安装额外的管家。与此相反，我们会安装多款播放器。那么，这是为什么呢？当然，也可以思考这样一个问题，好评的软件那么多，硬盘又足够大，为什么不都装上？看到第二个问题，思路似乎清晰了。很简单，解压软件、管家的功能大同小异，且都免费，甚至不需要考虑到底用哪个，似乎只要有那么一个就好了。但是，播放器有单机、网络之分。即使均为网络播放器，仍会搜索到不同资源...即使播放器之间看似相同。

在1996年，还在读书的Tim C. Hesterberg问斯坦福大学的统计学家Bradley Efron这样一个问题：“在统计学领域什么问题最重要？”他满以为Efron会回答给予他崇高地位的Bootstrap算法，结果Efron的回答却是变量选择。

　　用不同的软件类比不同的变量，装机变成了一个变量选择的问题，选择恰到好处的软件使用户满意度达到最大。

1.由多元线性回归建模说起

　　我们考虑这样的用户满意度评价问题：一款软件的满意度可由用户评分(0~5分)和专家评分(0~5分).用户评分有主观因素，不同用户对同一软件的评分一般不同。专家评分会系统地考虑产品、技术等层面，更为客观，即对同一软件的评分可认为是相同的。我们将用户评分与专家评分的乘积表示一位用户对一款软件的满意度。乘积可以综合用户体验与实际价值，又可以让二者相互制约，更能反映出真实的用户满意度。那么，如果我们有用户的总体满意度以及他们对软件的评分数据，能不能通过数据估计出每款软件的专家评分？即能不能通过建立回归模型客观地得到软件优劣？

　　假设用户数为n软件数为p.根据上面的主观与客观评分假设，我们用列向量y=(y₁,y₂,...,y_n)^T表示每一位用户的满意度；矩阵X有n行p列，第i为用户i对p款软件评分为x_i=(x_i1,x_i2,_...,x_ip)；专家评分表示为β=(β₁,β₂,...,β_n)^T.很显然，满意度评分问题的模型是y=Xβ+ε,ε代表误差项。我们要通过一组包含用户满意度-评分的数据估计出β .似乎理论上可以得出客观层面的软件优劣。

2.一个简单的模拟实验

　　我们仍然运用最小二乘法，与上一篇相比，这次是使用多元线性回归的最小二乘法。不过道理相同，获得向量β的估计值，每一位用户评分带入都会得到该用户满意度估计值，并使全部用户的满意度估计值与真实值的误差平方和达到最小。

　　回到第一段的问题一，我们假设只研究两款压缩软件x₁,x₂.根据问题一的假设，由于用户觉得他们二者不存在差异，因此对两款软件的评分会非常接近。但专家从客观层面评价二者还是有一定的区别的，对两款软件的评分是β₁=3.5和β₂=4.5.那么用户满意度的真实模型为y=3.5x₁+4.5x₂+ε.假设有10位用户，且用户间的评价存在一定差异，根据本段做出如下表格：

用户	1	2	3	4	5	6	7	8	9	10
x1评分	1.7	2.0	2.3	2.5	2.7	3.3	3.8	4.3	4.6	4.9
x2评分	1.7	2.2	2.4	2.6	2.9	3.1	4.0	4.1	4.8	5.0
εi	0.9	-0.5	0.5	-0.6	0.4	2.1	1.7	0.4	-1.7	-1.3
yi	14.50	16.40	19.35	19.85	22.90	27.60	33.00	33.90	36.00	38.35

　　在R语言中，我们建立多元线性回归模型对β₁,β₂进行估计:

x1 <- c(1.7, 2.0, 2.3, 2.5, 2.7, 3.3, 3.8, 4.3, 4.6, 4.9);
x2 <- c(1.7, 2.2, 2.4, 2.6, 2.9, 3.1, 4.0, 4.1, 4.8, 5.0);
e <- c(0.9, -0.5, 0.5, -0.6, 0.4, 2.1, 1.7, 0.4, -1.7, -1.3);
y <- 3.5 * x1 + 4.5 * x2 + e;
model <- lm(y ~ x1 + x2)
summary(model)

Residuals:
Min 1Q Median 3Q Max
-0.9534 -0.6940 -0.2868 0.4040 2.2507

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.7315 1.1518 1.503 0.1765
x1 7.0096 2.3947 2.927 0.0221 *
x2 0.5953 2.4084 0.247 0.8119
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.125 on 7 degrees of freedom
Multiple R-squared: 0.987, Adjusted R-squared: 0.9833
F-statistic: 265.9 on 2 and 7 DF, p-value: 2.501e-07

 　　真实模型为：y=3.5x₁+4.5x₂+ε.

　　最小二乘法回归模型为：y=7.0096x₁+0.5953x₂+1.7315.

　　二者相差如此之悬殊，但模型的调整后回归系数(Adjusted R-squared)却达到了0.9833,模型严重失真，但拟合效果仍是很好的。当然，我们的真实模型中没有引入常数项，如果有，恐怕x₂的系数β₂会被估计成负数。显然，之前规定了评分在0~5之间，那么回归结果会更明显地表现出是虚假的。那么，为什么会这样呢?原因很简单，数据中存在高度相关的变量(x₁,x₂的相关性高达0.987),这两个变量步调如此相似，像两条平行的向量，也就是说二者是共线的。通俗一些，由于两款软件太相似了，以至于无法判断谁能贡献出更大的用户满意度，二者10：0开，5：5开，0：10开几乎无任何差别。

　　从上面的结果也可以看出，β₁的标准误差达到了2.3947而β₂的达到了2.4084.即使最小二乘法的估计是无偏的，它也不再有效了。在上篇中我们说到了最小二乘法是无偏估计中最好的。这也暗示出为了估计的有效，我们会在一定程度上牺牲无偏性来换取有效性，采用岭回归、主成份等有偏的方法。

3.多重共线性是普遍存在的

　　在统计学或机器学习的一些截面数据的多元回归问题中，X为n×p的二维矩阵，但通常情况下p»n.这就是高维复杂数据，之所以引入大量的变量就是因为它们通常都有信息，但研究者并不清楚到底多少变量有用。变量多了，变量和变量之间会共线，也很容易出现一个变量被其他几个变量线性表述的情况(一个功能冗杂的软件被其他垂直细分但功能专精的软件代替),这种被代替情况就是所谓的多重共线性。我们需要进行变量选择，否则很容易造成虚假回归。

　　普林斯顿大学统计与金融工程的终身教授，"The Annals of Statistics" 杂志的主编范剑青教授在一篇论文中做过这样一个模拟实验：

 

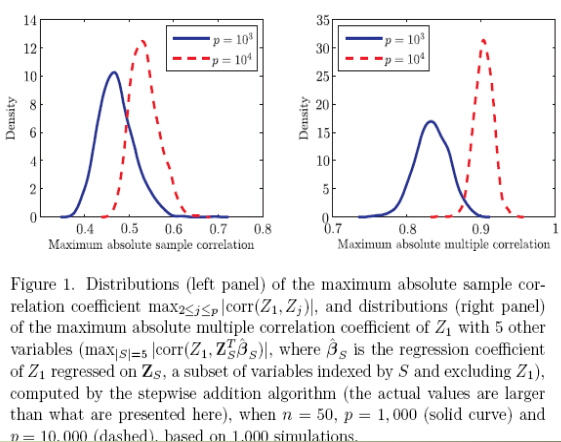
随机生成n=50,Z₁,...,Z_p~_i.i.d.的样本，分别计算p=1000和p=10000时的Z₁与Z_j,j≥2的相关系数绝对值中最大值以及分布(左图),以及的Z₁与其他5个变量的多重相关性绝对值中的最大值以及分布(图右).不难发现，无论1000个变量还是10000个变量，随机模拟出的变量几乎没有与Z₁共线的，即几乎没有与Z₁高度相关的。即使变量数增加了10倍，出现更高相关性的可能也未增加太多。但是，从随机模拟出的1000个变量中任选5个非Z₁变量进行线性组合，都很容易与Z₁高度相关，即产生了多重共线性。当变量数达到了10000时，多重共线性发生的概率更大了，而且相关性也普遍增强了。

　　很显然，无论是1000个变量还是10000个变量，相对于实际问题，变量数并不大。在随机模拟实验下，高维数据的多重共线性都会100%存在，况且，实际问题会这样的随机么？