Flows
\(\mathscr{FLOWS}\)
我知道这个标题的字体花里胡哨,我错了
执笔于2024年1月11日,15:46。
本来昨天都该开始弄这个的,但是由于补模拟赛的毒瘤题搞到现在。
作者开始写这篇笔记时的水平可以理解为只会背 dinic 的板子。只能做提高+难度的网络流。由于学习的跳跃性,笔记也会有些跳跃。
本文源码长度已经于2024年1月20日达到32KB,大概是dyx大佬的学习笔记的一半(((未来可能会进行小规模更新,但现在暂时停工了。如你所见,目前这篇笔记还是半完成状态。
结论
Dinic算法会使得结束后,割到S的部分尽量少。
(待补充。。。)
算法
消圈算法
冷门科技,但在我所做过的有负圈的费用流题目中表现良好,甚至可以拿下模板题的最优解。
(待补充。。。)
消圈算法 && 有负圈的费用流模板。
我的思路比较神必。
枚举行列的限制,就可以知道答案的限制。
行和列这个 “放置数量相等” 比较烦。考虑直接变成
“行的数量 - 列的数量 = 0” 。
想到了什么?欧拉回路,每个点的出度和入度之和相等。
那么我们可以直接把行和列缩成一个点,边 $(i \rightarrow j) $ 表示 \((i, j)\) 有一块芯片。
这样每个点 \(out - in\) 为 \(0\) 就相当于在图上添加一些回路。每经过一条边就有 \(1\) 的费用。跑无源汇最大费用可行流。
有些点必选?你可以用上下界网络流的方法让这条边必选,更简单的方法是直接把费用设为 \(inf\) 。
行和列有最大值限制?没问题,我们进行拆点,把每个点拆成入点和出点,中间连上一条流量为 \(lim\) 的边就可以了。
原始对偶算法
原始对偶算法可以在 \(\Theta(fn \log n)\) 的时间复杂度内算出一张图的最小费用最大流。但是前提是初始图上的所有边都非负。(如果有负权边,那么一开始要跑SPFA)
算法流程很简单,第一轮增广的时候先使用 dijkstra 算法计算源点到每个点的最短路。设置每个点的“势能” \(h_i = dis_i\) ,在之后每轮增广的时候,图上可能有负权边,只需要利用 Johnson 负权最短路的思想,把每条边的边权视为 \(h_i + w(i, j) - h_j\) 进行求解即可。
但是与普通最短路不一样的地方是:我们需要进行边权的改动。
定理:每次进行dijkstra算法后,将每个点的 \(h_i\) 加上 \(dis_i\) 作为新的 \(h'_i\),则 \(h'_i + w(i, j) - h'_j\) 都非负。
证明:
分边的来源考虑,可能是原来就存在的边,也可能是因为增广出现的反向边。
如果是新出现的反向边 \((j, i)\),那么满足 \(dis_i + (h_i + w(i, j) - h_j) - dis_j = 0\) ,变形后满足 \((dis_j + h_j) + w(j, i) - (dis_i + h_i) = 0\),显然满足要求。
那么如果是原来就存在的边,满足 \(dis_i + (h_i + w(i, j) - h_j) - dis_j \geq 0\) ,显然用 \(h_i + dis_i\) 作为势能非负。
二分图最小点覆盖
\(K \ddot onig定理\) :二分图最大匹配=最小点覆盖。
证明:建出网络流模型,由两个问题的建图一模一样得证。
(待补充。。。)
KM算法
按理来说不该在这里的。但是因为一起学了就放在这里了。这里 有挺不错的代码实现。
这个算法是用来求二分图最大权完美匹配的。在这之前你要会 BFS 求二分图最大匹配,很奇怪对吧,但是没有这个做不了。
一些记号的定义如下:
\(px, py\):分别记录左侧点和右侧点的匹配对象。
\(vx, vy\): 分别记录当前这轮增广中某个左部点和右部点是否被增广过。
\(pre\): 记录右部点在搜索树上的前驱。
枚举每个点进行BFS增广,增广前清空 除了 \(px\) 和 \(py\) (记录当前的匹配情况)以外的所有数组 并把当前点加入队列。每次弹出队首 \(u\) ,遇到一个没有被遍历过的右部点就把它的 \(pre\) 设置为当前队首 \(u\) ,标记它为被遍历过,然后检查它的匹配情况,如果它没有被匹配,那么就匹配它,沿着右部点的 \(pre\) 和左部点的 \(px\) 更新 \(px\) 和 \(py\)。返回增广成功。否则就把它的匹配点加入队列,继续匹配。如果队列为空,增广失败。
这玩意有什么用呢?
KM = BFS求最大匹配 + 扩大相等子图。
在这之前,要讲解一些概念。
交错树
在寻找增广路的过程中,每个左部点 \(a\) 向它尝试增广的右部点连边,右部点 \(b\) 向 \(py_b\) 连边,可以形成一棵树。这棵树就叫交错树。在下面的算法中,可以认为 \(vx_i = 1\) 和 \(vy_i = 1\) 标记一个点在交错树中。
顶标
为每个左部点设置 \(wx\) ,为每个右部点设置 \(wy\) ,使得 \(wx_a + wy_b \geq w(a, b)\) 。的 \(wx\) 和 \(wy\) 叫做一组顶标。
相等子图
把图中满足 \(wx_a + wy_b = w(a, b)\) 的边构成的子图叫做相等子图。
定理:相等子图中任意一组完备匹配是该二分图的最大权完美匹配。
证明:任何一组匹配都满足 \(\sum w(a, b) \leq \sum wx_a + \sum wy_b\) 。如果这时在相等子图中存在完美匹配,那么不等式可以取等,得证。
那么我们的目的很明确了:寻找增广路,扩大相等子图 。
我们记一个右部点的 \(slack_i = min_{j}(wx_j + wy_i - w(j, i))\),那么当一个点的 \(slack = 0\) ,相等子图中有一条指向它的边。
在一轮BFS的过程中,我们还是弹出队首,记为 \(u\) 。比求最大匹配多出的步骤是:我们需要对每个不在交错树上的右部点更新它的 \(slack_i\) 。如果 \(slack_i = 0\) 就意味着这条边在相等子图里,标记 \(i\) 进入交错树,然后按照求最大匹配相同的方法做就行了。但是要注意的是 无论如何都要把它的 \(pre_i\) 设置为 \(u\) ,因为可能这条边当前不在相等子图里,等顶标更新过后就在了,但是这时已经不知道 \(i\) 在交错树上的父亲是谁了。
如果在队列为空之前增广成功,我们直接返回,否则我们进行顶标的修改。找到没有被加入交错树中的 \(slack_i\) 中最小的一个,记为 \(d\),(当然,如果所有点都在交错树上,那么增广必然失败,也返回。)对于交错树上的每个左部点,\(wx\) 减少 \(d\),同时,交错树上的每个右部点 \(wy\) 增加 \(d\) 。
我们分类讨论这可能对 \(slack\) 产生的变化:
一条 \(vx_l = 1, vy_r = 1\) 的边:\(slack_r\) 不变 。这是一条交错树上的边。
一条 \(vx_l = 0, vy_r = 0\) 的边:\(slack_r\) 不变 。这条边还没有与当前交错树产生联系。
一条 \(vx_l = 0, vy_r = 1\) 的边:\(slack_r\) 增加 。这可能导致一条边被移出相等子图。
一条 \(vx_l = 1, vy_r = 0\) 的边:\(slack_r\) 减少 。这可能导致一条边进入相等子图。每轮至少会发生一次这样的情况。
对于每个不在交错树上的 \(slack_i = 0\) ,我们都执行一次“能匹配就匹配,匹配失败就把它的匹配点入队”的过程。
分模块进行复杂度分析。总共会增广 \(n\) 轮,每轮会遍历整个图一次,复杂度是 \(\Theta(n^3)\)。
但是,每次扩大相等子图要花费 \(\Theta(n)\) 的时间,那么这部分复杂度是 \(\Theta(n * (扩大相等子图次数))\) 。这里,我能找到的所有资料都表示相等子图只会扩大 \(n^2\) 次。可是,上面的分析过程明明显示有些边可能会被移出相等子图,不能按照每轮一定会有一条边进入相等子图进行分析。我本来试图证明这种情况出现的次数不会很多,但是经过我的构造,发现这样的情况是普遍的。那一定是有高妙的我想不到的势能分析了。
这里的东西可能在久远的未来会有所补充,但现在碍于个人水平有限,无法给出解答。怀着和我同样疑惑看到这里的人,对不起,让你们失望了。
如果有人会证明这个东西的正确性或者有什么好的想法,欢迎和我交♂流。
带花树(一般图最大匹配)
跟在KM后面比较恰当,因为前置知识都是BFS求二分图最大匹配。
带花树 = BFS求最大匹配 + 缩花。
我们记图上的一个奇数大小的环为“花”,带花树算法的核心思想就是在 BFS 的过程中一朵“花”就把它缩成一个点。
我们考虑正常的二分图中 BFS 的过程:从一个左部点开始,寻找与它相邻的右部点,如果可以增广,那么进行一次增广,否则把它的匹配点加入队列。
带花树算法类似,从一个 没有被匹配的 “1类点” \(u\) 开始,寻找与它相邻的点没有被标记过的点 \(v\) 标记为“2类点”,并标记它的 \(pre_v = u\) 。如果可以增广,那么进行一次增广,否则把它的匹配点加入队列。
我们宁静安好地进行这个过程,直到遇到一个奇数大小的环。
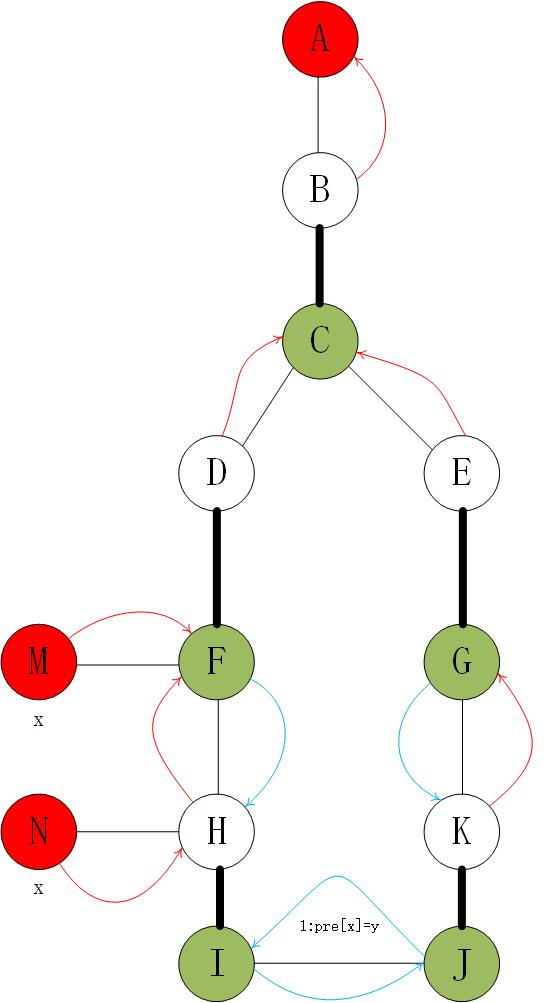
图是偷来的
I和J都是 1 类点,我们从 \(I\) 开始搜索相邻的点的时候发现了 \(J\) 。这个时候说明出现了奇环。我们发现,不仅可以沿着已有的边进行增广,还可以走 \(A \sim J \sim I \sim N\) 这条绕过环的增广路。但是环上与 \(N\) 相邻的点 \(H\) 因为是 2 类点没有被我们加入队列! \(pre\) 指针也是错的,这样就算我们找到了增广路也无法退回来。
这个时候我们直接把 \(FH, IJ, GK\) 之间的 \(pre\) 改成双向边。(蓝色的边是新加入的),并且把原先的 2 类点 \(D, H\) 改成 1 类点,把它们加入队列。拿 \(H\) 来举例子:如果它找到了增广路 \(N\) ,那么沿着 \(N \sim H \sim I \sim J \sim C \sim A\) 能退回到搜索的出发点 \(A\) 了!这就完成了一次增广。
同时,我们发现,在这个环上,任何一个点出发找到增广路之后,所有其它的点都会两两配对。所以这个环上的所有点其实都是等效的(可能出发点 C 除外)。我们考虑这个奇环的时候,其实我们在考虑的是一个“等效点”。所以我们可以把这个环缩成一个点。(注意:这里只是在考虑整个图的结构的时候缩点了,匹配边和 \(pre\) 这些信息还保留在环上)。
具体来说:我们每次遇到奇环,就求出两个端点 \(I,J\) 在 BFS 树上的 LCA ,记为 \(p\) 。(注意这个是缩花后意义的。)这一步可以暴力实现,每跳到一个点就会把一个点缩起来,复杂度有保证。(好像也没有什么办法优化)。特别注意细节:因为把奇环上的点 2 类点变成 1 类点入队的时候会访问到相邻的点(虽然这样做没有影响),所以两个点的 \(LCA\) 可能是自己。
然后我们要干三件事:重新连接 \(pre\),入队和缩点。这三件事都是可以直接从端点跳到 LCA 的过程中做完的。特别的,如果到了 LCA \(p\),就不要再反向建立 \(pre\) 了。
复杂度的话,每轮增广,每个点只会入队一次,最多因为缩点遍历所有点一次,所以复杂度是 \(\Theta (n^3)\) 的。(为啥并查集不算在复杂度里?好像是因为每个点每轮增广只会被合并 \(\Theta(n)\) 次,所以 find 操作最差一轮也只会递归 \(\Theta(n^2)\) 次,我不太懂,瞎编的。)
不算太简单。
把每个筐子拆成三个点,每个球向对应筐子的三个点连边。筐子内部三个点互相连边。跑一般图最大匹配。答案是最大匹配 - 球的个数。
为啥这样是对的呢?会不会有球没法匹配的情况呢?不会。因为让一个球变得合法最多减少一个半空的箱子。
据说,优先增广球所代表的点会让所有球都能匹配。这个不太懂,但是感性理解一下很对吧(((
Stoer-Wagner算法
全局最小割,但是好像和网络流没啥关系。
在这里 \(\textrm{ix35}\) 进行了一个大面积伪证,强烈谴责。看来三块Au也不能完全相信
观察最小割的性质:如果两个点 \(s, t\) 被割到同一个连通块内部,那么两条边 \((a, s), (a, t)\) 要么同时被割,要么不同时被割。原因显然:如果割断 \((a, s)\) 而不割 \((a, t)\) ,那么 \(a, s, t\) 仍然在同一个连通块内。
那么根据这条性质,可以进行 “缩点”。如果确定 \(s, t\) 会出现在同一集合内部,那么就可以删掉 \(t\) ,把 \(t\) 的所有边权加到 \(s\) 上。
现在,我们可以随意指定图上两点,求出它们的最小割(这个过程记为 MinimumCutPhase)。如果我们能做到 \(\Theta(n ^ 2)\) 的话,那么这两个点不在一个连通块的情况就确定了。剩下的在一个连通块的情况,我们直接“缩点”,迭代进行上述过程。就能在 \(\Theta(n ^ 3)\) 时间内通过本题。
一些记号:
\(A\): 一个点的序列。其生成方式是:先随意挑选一个点作为第一个点,每一次把 \(w(A, u)\) 最大的 \(u\) 加入 \(A\) 中。
\(A_u\): \(A\) 在 \(u\) (不含)之前的部分。
\(s, t\): A的最后两个元素。
\(C\): \(s\) 到 \(t\) 的最小割。
活跃顶点:在 \(A\) 中 和前一个元素不在 \(C\) 同一侧的点。
\(w(A, u)\):\(\sum_{i \in A}g_{i, u}\)
\(C_u\): \(C\) 在 \(A_u \cup u\) 中的 诱导割 (可以理解为在诱导子图中的边集)
\(w(C_u)\): \(C_u\) 的边权和。
定理:每一次 MinimumCutPhase 的过程中, \(w(C) = w(A_t, t)\) 。
先来证明一个引理:
引理:每个活跃顶点满足 \(w(A_v, v) \leq w(C_v)\) 。
考虑对所有活跃顶点进行归纳证明。
对于第一个活跃顶点 \(u\),不等式以等号成立。这是因为 \(u\) 和之前的所有点分居 \(C\) 两侧,最小割必须也只用割掉 \(u\) 和 \(A_u\) 中的所有边。
对于之后的每个点 \(v\),考虑它的前一个活跃顶点 \(u\) ,那么 \(w(A_v, v) = w(A_u, v) + w(A_v \backslash A_u, v)\)
由于我们按照 \(w(A, x)\) 从小到大加入顶点,那么有 \(w(C_u) \geq w(A_u, u) \geq w(A_u, v)\) 。
而由于 \(v\) 和 \(A_v \backslash A_u\) 中的点分处 \(C\) 两侧,那么中间部分必然产生 \(w(A_v \backslash A_u, v)\) 的代价。
所以有 \(w(C_v) \geq w(A_v \backslash A_u, v) + w(C_u) \geq w(A_v \backslash A_u, v) + w(A_u, v) = w(A_v, v)\),得证。
显然:由于引理成立,则由于 \(t\) 一定是活跃顶点,则有: \(w(A_t, t) \leq w(C_t) = w(C)\)
又因为割断 \(w(A_t, t)\) 中的所有边后, \(s, t\) 显然不连通,那么 \(w(A_t, t) \geq w(C)\)。
所以 \(w(C) = w(A_t, t)\) 。
\(\mathscr{Q.E.D.}\)
一些例题
被迫营业。每类中大概按照离谱程度升序排列。
最大流
相当反直觉的一道题。
这道题乍一看,题目对高清投影仪的限制更紧。毕竟它不仅可以在讲课中使用,还可以在研讨会中使用,用途更广泛,自然需求也就越紧张。
真 的 吗?
你会发现,如果给出一组普通投影仪的方案,我们可以很轻松的判断能否构造出一组高清投影仪的方案:直接判断每个时刻是否有超过 \(x\) 个需求即可。
为什么?
发现其实这个构造方案本质上是一个最小链划分问题,最小链划分=最长反链。一组反链是一组两两相交的区间。而如果一组区间两两相交,那么它们交于一点(不会证,但感觉很能感性理解。)upd:证明被yhy秒了。
所以我们只需要构造一组方案,使得每时每刻投影仪使用的数量都 $ < x$ 就可以了。
设:时刻 \(i\) 的需求数量是 \(sum_i\) ,那么至少要有 \(sum_i - x\) 个普通投影仪在此时被使用。那么最多 \(min(y - sum_i + x, y)\) 个普通投影仪在“休息”。然后我们从 \(i\) 向 \(i + 1\) 连边权 \(min(y - sum_i + x, y)\) 的边,\(p_i\) 向 \(q_i\) 连边权为 \(1\) 的边。那么如果某一刻,某台普通投影仪既没有研讨会可以去,又由于总数限制必须去研讨会,那么就无解了。对应到图上就是最大流不为 \(y\) 。
按理来说就没了,但是我们不妨做做脑筋体操。如果我们反过来做会怎么样呢?这样,每个点都会又三种选择:讲课,研讨会,休息。但是讲课是必须要讲满 \(n\) 堂的,所以感觉会有些离谱。相当不符合直觉,或者说:讲课只能用高清投影仪,反而简化了高清投影仪这部分的问题。
真就不会的时候会不了一点,会了不知道为什么不会呗。
最小割
首先建出最小割模型是容易的。每个人向他经过的树上的每一条边连边权为 \(inf\) 的边,然后每个人自己向源点连边权为 \(1\) 的边,每条树上的边向汇点连边权为 \(1\) 的边。树剖 + 线段树优化建图即可。这也能黑吗?/cf
感觉略套路。
每个点的最优选择是它的绝对值,根据最小割的传统艺能先选上。
有一件感性理解的事情是绝对值是很难在最小割的题里描述的,所以必然存在一些“不合法的一定不优”。
观察到如果把一个数 \(x\) 放到总和是正数的连通块里,它的贡献是 \(x\) ,否则是 \(-x\) (废话),如果我们钦定一个连通块的正负计算答案,那么在我们钦定错误的情况下算出来的答案是不优的。
那么建立集合划分模型。与源点相连的点是选择正数连通块,否则选择负数连通块。连接对应代价的边。这里会存在 \(0\) 权边的奇怪问题,先存疑(?)那么剩下的唯一限制是不能有相邻的两个点被划分到两侧。
这是容易的。把每个点拆成 \(i, i'\) 中间连接边权为 \(|b_i| + a_i\) 的边表示割掉这个点。那么相邻的边在图上表现为一条 \(x'\) 指向 \(y\) ,边权为 \(inf\) 的边。直接最小割即可。
ARC的F就这?ARC的F就这?ARC的F就这?ARC的F就这?ARC的F就这?
被巨长无比的题目描述骗了,做网络流做傻了导致的。
首先 \(\lfloor 10\ln(1 + A) \rfloor\) 是值域很小的,可以枚举之,最后得到一组方案再check一下相邻两者为异性的情况数量符合条件就好了。
然后不同层的点除了相邻两层之间需要判一下是不是异性是相互独立的,那么我们设计一个dp:\(f_{i, j, S}\) 表示第 \(i\) 层绵羊,已经有 \(j\) 头相邻绵羊性别不同,上一层的性别状态是 \(S\) 的最大收益。
这个 dp 枚举上一个状态转移是 \(\Theta(10\ln(NK)N^2K2^{2K})\) 的 这不是随便跑吗优势在我 。
然后就是计算每一层的代价的问题了。
每一头羊都有两种可能:雄性或者雌性。两头羊产生贡献当且仅当它们都不变性或者都变性。这是一个集合划分模型。如果我们设源点为雄性,汇点为雌性,则不满足集合划分模型的适用条件(划分到同一侧有价值) 所以应该设源点为变性,汇点为不变性,所有点向源点连边权为 \(c_i\) 的边,钦定要变性的点向汇点连边权为 \(\inf\) 的边,建立两排虚点,分别向有繁衍关系的点连边权为 \(\inf\) 的边,
它们分别向源点和汇点连边权为 \(b_j\) 和 \(\lfloor b_jd_j\rfloor\) 的边,跑最小割即可。
nodgd牛逼!nodgd牛逼!!nodgd牛逼!!! 人类叛变精华(什
上图。
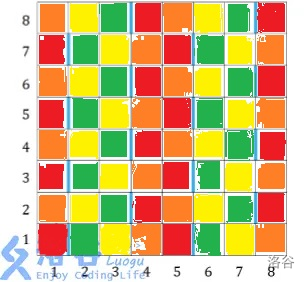
我也不知道为啥所有被讨厌的形状一定跨过四种颜色中的每一种恰好一次。那么我们就可以建立分层图。建立四排点,分别表示黄,红,橙,绿色的点。一条非法路径一定穿过这四排点各一次,其中至少要移除一个点,这就是最小割。
但这是点最小割,可以拆点,但没必要。黄绿两种点权可以放在它到源汇点的边上,红橙两个点一定一起出现,它们的点权可以取min,放在它们中间,这样就避开了拆点的问题。毕竟点数高达1e5,感觉拆点就要炸了 。
最大权闭合子图
首先二分答案,变成判定性问题。
存在一个图的“密度” 至少是 \(S\) ,那么就有 \(\frac{\mid E\mid}{\mid V\mid} \geq S\) 即
\(\mid E\mid - S \mid V\mid \geq 0\)
这意味着,我每选择一条边的代价是 \(1\) ,每选择一个点的代价是 \(-S\) ,每选择一条边,必须选择它的两个端点。
那么这个就是最大权闭合子图问题,以边为左部点,以点为右部点连边,建立一个二分图,直接跑就可以了。
[ARC161F] Everywhere is Sparser than Whole (Judge)
我也不知道应不应该放在这里/yun
检验是否存在最大密度子图 \(\geq D\) ?不行。因为原图本身的密度就 \(=D\) 。
没关系,我们来分析一波性质。
如果有一个子图的密度 \(> D\) ,那么它的 补图 一定满足 \(\frac{\mid E\mid}{\mid V\mid} < D\) (很简单,因为整体密度 \(= D\))
否则,所有子图的补图的密度一定 \(\frac{\mid E\mid}{\mid V\mid} \geq D\)
考虑怎样刻画一个 “补图” ,就是把某个端点在指定点集里的所有边并起来。
回到上面那道题的二分图,也就是每个右部点集的邻域都满足 \(\frac{\mid E\mid}{\mid V\mid} \geq D\) ,根据 Hall 定理,这个意味着右部点存在 D 重完美匹配 。
先以左部点向源点连边权为 \(1\) 的边,右部点向汇点连边权为 \(D\) 的边,跑一下多重匹配再说。如果没有完美匹配答案就是 No。
现在,我们只用判定是否存在一个子图的密度 \(= D\) 。
执行上面的匹配操作后,我们得到了一张残量网络。我们给这张网络上的边定向:如果某个左部点 \(u\) 匹配右部点 \(v\) ,那么 该边从 \(v \rightarrow u\) ,反之 \(u \rightarrow v\) 。
对这张重定向后的图进行缩点,原图非法当且仅当存在不止一个强连通分量。
也就是说,新图的某个子强连通分量一定对应一个密度为 \(D\) 的子图,一个密度为 \(D\) 的子图也一定对应新图的一个子强连通分量。
先证明前面部分:我们取没有出边的强连通分量,它所有结点的出边都指向内部。又因为取出的每个右部点匹配的 \(D\) 个左部点两两不同,意味着这些右部点在原图上对应 \(DN\) 条边,且这 \(DN\) 条边相邻的点都在图内部,那么我们取出的恰好是一个子图,且密度为 \(D\)。
再证明后面部分:如果取出的子图不连通,取出其连通的部分,由于取出的是子图,那么所有边对应的左部点的出边指向图内部。又因为取出的恰好有 \(N\) 个点 \(DN\) 条边,那么所有点对应的右部点的出边(即匹配边)也只能指向内部,否则会导致某个左部点没有被匹配。那么我们取出的子图对应一个强连通分量(这里别人写的是一个,但我感觉多个也可以?),证毕。
感觉像是某个论文题。
费用流
显然只要每个人摧毁的点都单调递增就可以保证最终摧毁的点了。
首先对原图进行floyd,注意这里要求 \(i\) 只能通过小于 \(i\) 的点到达 \(j\) 。
然后对于每一对 \(i < j\) ,连一条流量为 \(\infty\) ,费用为 \(dis(i, j)\) 的边,表示从 \(i\) 出发摧毁 \(j\) ,直接对源点跑流量为 \(K\) 的最小费用最大流即可。
感觉完全不到黑 /cf
老套路题了。但我把套路忘了赶紧回去复习了一下
首先完全图上的这种三元环计数是可以直接算的。三元环数量是 \(\frac{(n)(n - 1)(n - 2)}{3} - \sum(\frac{deg_i(deg_i - 1)}{2})\),其中 \(deg_i\) 是每个点的出度。原理是每个非法三元环唯一对应同一个点的两条出边。
所以我们需要最小化每个点的胜利场次数量的一个二次函数之和。左转P4307包教包会。先假装所有球队全部输了,然后为每场比赛建一个点,向汇点连流量为 \(1\) ,费用为 \(0\) 的边,表示每场比赛有唯一赢家。
计算二次函数的变化量,从 \(i\) 号球队向一个虚点连剩下的比赛数量条边,分别流量为 \(1\),费用为赢得 \(i\) 场比赛的新增费用。从虚点向所有可能的比赛连流量为 \(1\) ,费用为 \(0\) 的边,表示参加一次比赛。由于费用流的贪心性质,最后每个球队的所有有流的出边一定构成一段前缀。然后就没有了。
利用 原始对偶算法 可以在 \(\Theta(fm \log n)\) 的时间复杂度内求出一张初始无负权边的图的最小费用最大流。
首先一个 SCC 内部的点互相可达,先缩点变成DAG。
容易建出费用流模型,流量为 \(k\) ,保留原图的边,费用为 \(0\),流量为 \(\inf\) ,每个点拆成出点入点,连费用为 \(0\),流量为 \(\inf\) 的边和费用为 \(-a_i\),流量为 \(1\) 的边。所有点向汇点连边,跑最小费用最大流。
但是图上带负权边。怎么会是呢?
高情商做法:
一个显而易见的想法是:我们改为计算每走一步的 “损失” 。这样边权就非负了。但是这张图是一个DAG,每走一步损失怎么定义呢?
魔法来了:我们对原图进行 拓扑排序,一条路径显然只能从拓扑序小的点走向拓扑序大的点。所以如果走一条边 \((i, j)\) ,那么 \((ord_i, ord_j)\) 之间的点必然全部无法到达(!!!)那么我们放弃拆点,而是直接利用原图的边,把每条边的费用设为 \(\sum_{k = i + 1} ^ {j - 1}{a_{ord_k}}\) ,注意连向汇点的边也有边权。然后就没了。
优雅,实在是太优雅了!
但是我们同时有更适合我的低情商做法:注意到原图是DAG,我们进行一遍DAG上dp就能跑出初始最短路了。
AT的官方题解情商十分的高。
P6967 [NEERC2016] Delight for a Cat
区间选择模型。
以下内容摘抄自ix35的博客。要求全文背诵。
给定 \([1, m]\) 中的 \(n\) 个区间 \([l, r]\),每个区间选择一次的代价是 \(w_i\) ,最多可以选 \(c_i\) 次,要求任意点 \(j\) 被覆盖的次数在 \([a_j, b_j]\) 间,求最小/最大代价。
将 \([1, m + 1]\) 串成一条链,用 \(i \rightarrow i + 1\) 刻画每个点被覆盖的次数。
对于每个区间,建立 \(l_i \rightarrow r_i + 1\) 的一条边。称为区间边。如果区间边上有一条流,说明选择了这个区间。
源流向 \(1\) ,\(m + 1\) 流向汇。设置流量为极大值 \(X\) ,如果选择了 \(f_i\) 个跨过 \(i\) 的区间,那么就有 \(i \rightarrow i + 1\) 的流量为 \(x - f_i\) 。
那么每个点被覆盖 \([a_i, b_i]\) 次,对应到原图上就是 \(i \rightarrow i + 1\) 的边被流经 \([X - b_i, X - a_i]\) 次。上下界费用最大流即为答案。
以上内容摘抄自ix35的博客。要求全文背诵。
剩下的费用和流量都是容易的,故不再叙述。
核心思想:传递贡献。可以把 \(i \rightarrow i + 1\) 的流量视为 \(i\) 没有被覆盖的次数 ,那么如果没有区间的加入和删除,这个次数保留到下一个点。否则就做出对应的调整。
回到这道题,先假设每时每刻猫都在睡觉,交换区间和点,把区间覆盖点变成点对一个范围的区间做贡献,就完全是上面的东西了。设置 \(X = b_i\) 可以避免上下界。
CF132E Bits of merry old England
*2700。
2 hard 4 me.
源点向每个要输出的数字连流量为1,费用为 \(bit_i\) 的边,表示先强制钦定要每次新使用一个变量。
然后 \(i\) 向 \(i + 1\) 连一条边,流量为 \(k - 1\) ,费用为 \(0\),表示当前位置最多只能保留 \(k - 1\) 个点到下一轮。
接下来,再新建一排点 \(i'\) 向汇点连流量为1,费用为 \(0\) 的边。从 \(i\) 向 \(i'\) 连流量为 \(1\) 费用为 \(0\) 的边,表示输出一个变量后就放弃它。
最后,对于每个 \(i\) 和上一次相同的数出现的位置 \(j\) ,从 \(i\) 向 \(j'\) 连一条流量为 \(1\) ,费用为 \(-bit_i\) 的边,通过一个 \(j \sim i \sim j'\) 的流表示将上一次的变量保留到这一次,从而撤回一个费用。不用担心 “保留了错误的变量”之类的问题。因为如果这条边中间 \(j \sim i\) 的边断流是一定不优的。
跑最小费用最大流。
极为巧妙,不知道是怎么想到的。
模拟网络流
\(\textrm{flowerletter}\) 模拟赛T2 lis
首先容易转化为最小割模型,每个点向能和它组成 lis 的上一个点连边权为 \(\inf\) 的边,同时每个点拆成入点和出点,中间连边权为 \(1\) 的边,跑最小割即可。可以得50分。
注意连边过程非常有特点,一定是向 \(dp_j = dp_i - 1\) 的一些点连边。
容易发现 \(dp_j\) 相等的点一定单调不升 (我没发现) ,这意味着把 \(dp_j\) 相同的点拍到一起,每次连边的一定是一段区间。可以数据结构优化建图,又有25分。
正解则还依赖一个观察:对于 \(dp_i\) 相等的那些点,它连出去的区间的左右端点是单调的。这启发我们在分层图上模拟网络流。注意到如果我们每次尝试增广,都走最靠边的一条增广路,退流一定不优。(交叉的增广路可以换回来)。直接模拟即可。
感觉找不到比这更适合做模拟网络流入门题的题目了。
这个真的很巧妙。不过见过一次下次就能会了吧。
(待更)
切糕
不会切糕,精通切糕。
切糕模型 用来解决一类 每个变量有多个决策 且 不同变量的决策的值域之间存在限制 的最优化问题。(当然,要求这些限制比较特殊,不然可能没法建图。)
每个位置 \((r, c)\) 都有 \(h\) 个决策,即切割的高度,这是满足第一个条件的。我们从源点到汇点拉出 \(PQ\) 条链,每条链上有 \(R - 1\) 个点,从 \(1\) 开始编号,记源点为 \(0\) 号点,汇点为 \(R\) 号点,那么割断 \(i\) 和 \(i + 1\) 之间的连边表示在当前切糕上 \((r, c)\) 位置选择高度为 \(i + 1\) 的位置切割。
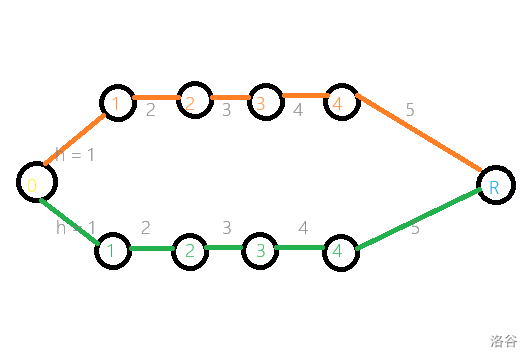
然后相邻两个位置之间存在限制,怎么办呢?
我们把限制写成两种:
- 如果 \((r, c)\) 选择了高度 \(h\), 那么 \((r', c')\) 不能选择高度大于 \(h + d\) 的位置。
- 如果 \((r', c')\) 选择了高度 \(h\), 那么 \((r, c)\) 不能选择高度大于 \(h + d\) 的位置。
这两种限制十分的对称,那么其实只用看第一个限制就行了。这个限制对应到图上就是:
如果 \((r, c)\) 的位置在 \(i\) 号点之前,那么 \((r', c')\) 割的位置在 \((i + d)\) 之后不合法。
那么就从 \((r', c')\) 的每一个位置 \(i + d\) ,向 \((r, c)\) 的位置 \(i\) 连接一条边权为 \(\inf\) 的边,防止同时割断这两个位置就行了。(当然,没有对应位置的就不连。)
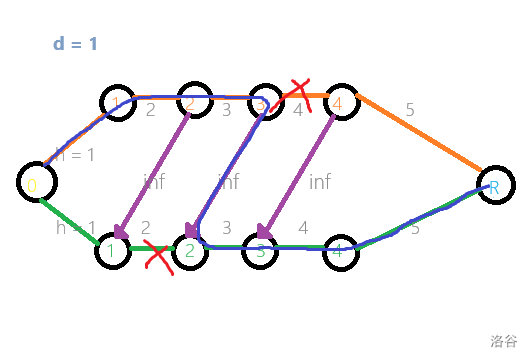
如果我割断两个不合法的位置,那么图上还存在一条连通的路,这就不是最小割。
你说得对但是
为啥这样是对的呢?
我们这样做,用了一个很重要的假设:在最小割里,每一行只会切割一次。如果不是这样,我们的做法就不成立。
如果我们在每一行上加 \(R\) 条边 \((i, i - 1, \inf)\) ,就可以避开这个问题,容易证明每条边只会被切割一次。
引理:最小割的每条割边 \((u, v)\) 满足:在残量网络上 \(S \rightarrow u, v \rightarrow T\) 。
证明:显然,如果二者之一不满足,去掉这条边更优。
回到原题,如果我们割掉了同一行上的两条边,图大概就会长成这样,然后 \(S\) 和 \(T\) 就连通了,不符合割的定义。
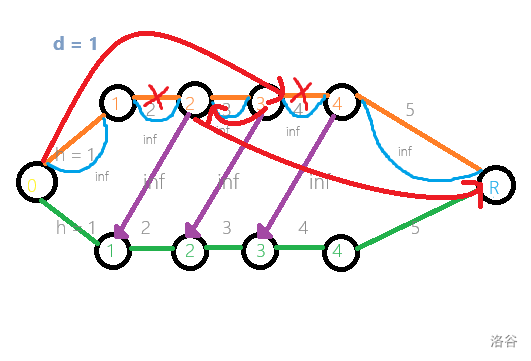
然后带着这种思路,我们删掉这些新加的边权为 \(\inf\) 的边,为啥还是对的呢?
有很重要的一点是:所有边权为 \(\inf\) 的边,都是从右向左指的(或者至少在同一列)。
那么,如果在同一列上割掉了两条边,那么右边那条边的起点(记为 \(y\))和 \(S\) 相连,左边那条边的终点(记为 \(x\))和 \(T\) 相连。
显然,\(x\) 不可能是通过一直向右走来和 \(T\) 相连的,(否则会走到 \(y\) 使得 \(ST\) 连通)。那么它只能是在中间的某个位置向左下拐弯了。但是,\(y\) 和 \(S\) 相连,那么它向左下连的那条边的终点也会和 \(S\) 相连,相当于 \(x, y\) 换了一行,变成了 \(x',y'\) ,它们的位置向左移动(也可能不移动),但是 \(y'\) 在 \(x'\) 右边的关系没有改变,除非它们中间又出现了一条新的割边,但是这样把 \(y'\) 换成新的那条割边的左端点就行了。无论如何 \(x'\) 又要重复开始一次寻找到 \(T\) 的道路的过程,而这个过程永远不会成功,也就证明了建图的正确性。
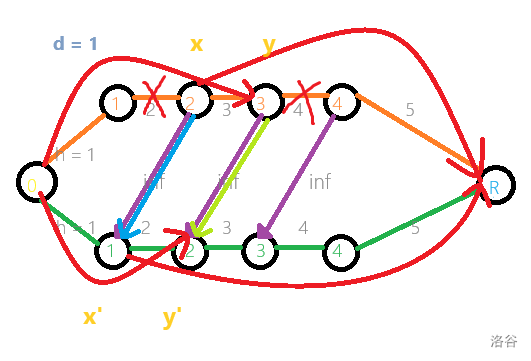
如果这些边不是从右往左连的话,还真有可能会在同一行割两条边,要特别注意。
其实 dengyaotriangle 大佬写的比我清楚多了,建议参考QwQ。
不知道这个算不算切糕(?)
从源点出发连出 \(n\) 条点数分别为 \(5\) 的链,记源点为 \(0\) 号点,第 \(i\) 号点和第 \(i - 1\) 号点之间的连边是升到等级 \(6 - i\) 的代价。
限制形如 “如果某条链割断的位置在 \(6 - L_{i, j}\) 右侧,那么就不能产生 \(a_i\) 元的收益”。
那么所有等级的 \(6 - L_{i, j}\) 号点向 \(i\) 号点连边权为 \(\inf\) 的边,\(i\) 号点向汇点连边权为 \(a_i\) 的边。
答案记为总奖励金额减去最小割。
(待更新。。。)
那玩意也能叫切糕吗?
——tanyulin
根据数据范围和“每行每列至少选择一个点”可以猜测这道题要使用网络流,但是其实猜到这题是网络流还是挺难的。
对于每个没有被选择的点,有两种限制:
\(r_x > w_{x, y}\) 与 \(c_x < w_{x, y}\) 恰好满足一个,
\(r_x < w_{x, y}\) 与 \(c_x > w_{x, y}\) 恰好满足一个。
注意到这个 “恰好” 其实是可以改成 “至少” 的。
\(r_x > w_{x, y} \lor c_x < w_{x, y}\)
\(r_x < w_{x, y} \lor c_x > w_{x, y}\) 。
这个时候,我们把等号加回去,然后去掉“没有被选择的点”,就能得到一个对所有点通用的限制:
\(r_x \ge w_{x, y} \lor c_x \le w_{x, y}\)
\(r_x \le w_{x, y} \lor c_x \ge w_{x, y}\) 。
然后我们建图满足这两个限制。把每个点拆成入点和出点,中间连边 \(n - c_{x, y}\) 。然后对于每一行,从源点出发,把元素从小到大串联起来,并且和汇点相连。边权 \(\infty\) 。每一列同理。
这样就能保证:
每行每列至少割一条边。(否则存在 \(S \sim 1 \sim 2 \cdots n \sim T\)) 的路径。
每行 $ \geq w_{x,y}$ 和每列 \(\leq w_{x, y}\) 至少割一条边。(否则存在 \(S \sim 1 \sim 2 \cdots w_{x, y} \cdots n \sim T\)) 的路径。
每列 $ \geq w_{x,y}$ 和每行 \(\leq w_{x, y}\) 至少割一条边。(同理)
用 \(n^2\) 减去最小割即可。
最后是为什么每行每列只会割一条边。由于存在只割 \(n\) 条边的方案(选择 \(n\) 个 \(n\)),每行每列又一定至少割一条边,如果每行每列不止割一条边,那么这个割就至少是 \(n^2\) 了。



