LCT
LCT学习笔记
摘要:肝了大半天的内容,属于任性。
splay
maintain
就是维护size罢了。
get
返回是父亲的左儿子还是右儿子。
clear
多测清空你都会,不信这个你不会。
rotate
是和Treap的操作一模一样的吧,,不过是站在儿子的角度旋转的吧。
为了避免出错:记住以下需要更新的内容(y为x的父亲,z为y的父亲):
- y的同侧儿子
- x的异侧儿子的父亲
- x的异侧儿子
- y的父亲
- z的儿子
- x的父亲
以上两两是一对。
记住特判x的异侧儿子和z不存在的情况。
splay
体谅一下作者祭天的绘图水平
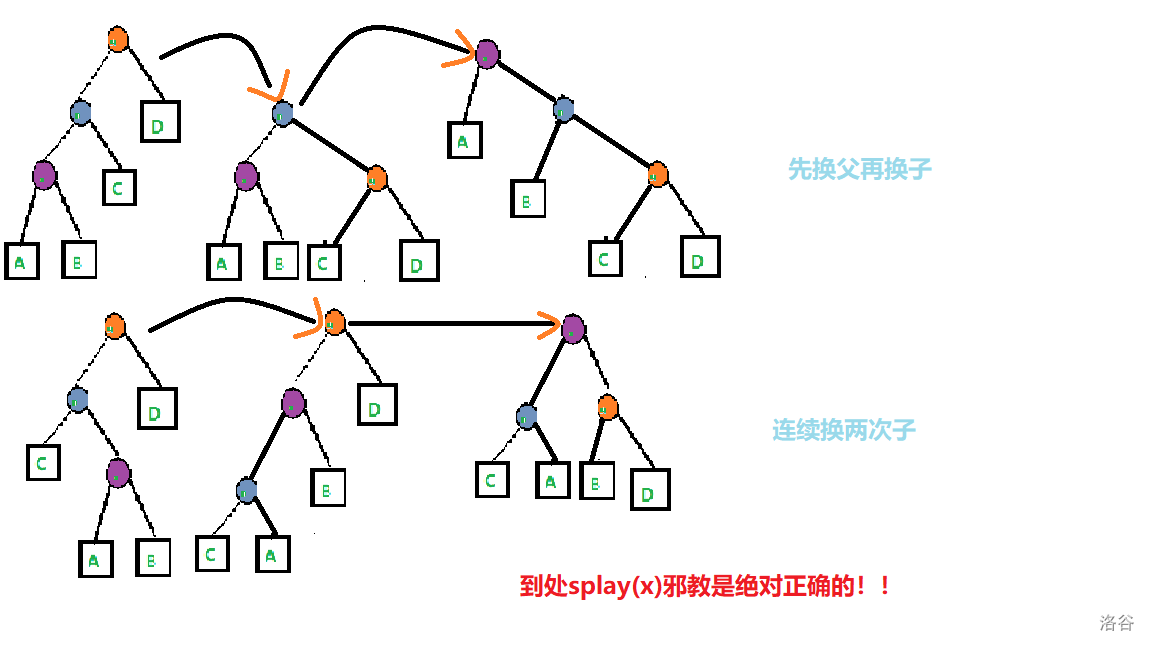
到处splay(x)邪教是绝对正确的!!!
简单来说:如果父亲和爷爷(先姑且这么叫)在一条直线上,那么先换父。否则先换子。
下方是OI-wiki上现有的代码。
void splay(int x) {
for (int f = fa[x]; f = fa[x], f; rotate(x))
if (fa[f]) rotate(get(x) == get(f) ? f : x);
rt = x;
}
代码压行到了丧心病狂的程度:一次循环里,先把 \(f\) 赋值为 \(fa_x\) 检验其是否存在。如不存在,退出循环。再判断是否存在爷爷,如果不存在只单旋,否则按上方规则双旋。
势能分析
建议别看,全是贺的。
这里是题外话:为了证这个复杂度,我先是在OI-wiki上看,但Oiwiki不靠谱的天然特性使得我成功的没有看懂。然后 \(\textcolor{black}{\_}\textcolor{red}{lazytag\_}\) 给我推荐了这篇博客,虽然写的很好,但是“同理可得”得不了让菜菜的我很心痛。最后我是在这里看懂了式子的推导,但是我对势能分析证复杂度理解不深,想不明白那个 \(\Theta(\log n)\) 的变化量和时间有什么关系,,,最后我自己yy了亿下终于找到了一种合理的解读!incredible!
感觉有希望成为全网最详细的解读了!
设 \(w_x = \log(size_x)\) ,初始势能 \(\varphi_0 = \sum w_i \leq n \log n\) 。末势能同理。
我们考虑求出一次Splay后 势能变化量和时间消耗的总和。(注意定义)
一次zig:
\(1\) 为时间消耗,其余部分为势能变化,下同。
一次zig-zig(g为爷爷)
注意:这里的“1”不能省略掉,因为不知道zig-zig的次数是多少。如果不能靠势能内的东西摊掉这个“1”,就会出现“ \(\Theta(n^2)\) 个常数” 的情况。
引理1:\(w_x+w'_g-2w'_x \leq -1\)
证明:
特别说明:第一个不等号请看图理解。
原式加上非负数:
一次zig-zag
引理2: \(w'_{fa}+w'_g-2w'_x\ \leq -1\)
证明(同样看图理解):
然后如法炮制:原式加上非负数
所以:一次splay的势能变化量和时间消耗之和是:
每次在平衡树上的操作的时间消耗和splay的时间消耗是同级的,就可以算进splay的常数里去。
由此可以看到:当时间消耗很大的时候,势能变化量为负 。
假定操作数量 \(m\) 和 \(n\) 同级,那么总共splay的势能变化量和时间消耗之和是 \(\Theta(n \log n)\),又因为势能变化在 \(\Theta (n \log n)\) 的范围内,所以总时间消耗是 \(\Theta(n \log n)\) 的!完结撒花!
code(文艺平衡树)
LCT
什么?这不是平衡树,这是LCT,遇到蒟蒻变大变高,劝退蒟蒻超好用的。先做做Sone1,再做做动态图连通性。什么?在哪里学?点击下方markdown笔记,学LCT送ETT,超实惠的。
what to solve?
链修链查询,换根换父亲。动态加删边,合并和分离。
更多用法等你发现(雾
peculiarity
- 虚实链剖分,每棵splay维护一条链,中序遍历splay得到的链的深度单调递增。
- “认父不认子”,每个点的splay只能访问其一个儿子,其他儿子所属的splay的根节点拉一条虚边指向这个儿子的父亲。


没错盗图就是快乐。
access
核心操作。LCT要维护的东西是很复杂的,(树的结构整体都在改变),所以LCT的思想是很暴力的,修改或查询一条链,就把它放在一个完整的数据结构里。当然这个数据结构是splay。
从树上拉出一条实链的过程其实不复杂:(摘自) \(\textcolor{black}{f}\textcolor{red}{lashhu}\) 的博客
inline void access(int x){
for(int y=0;x;y=x,x=f[x])
splay(x),c[x][1]=y,pushup(x);//儿子变了,需要及时上传信息
}
其中 \(f_x\) 是x在LCT上的虚边父亲。这里边比较玄妙的是 \(f_x\) 也可以表示实边的父亲,但两者的区别在于父亲认不认。所以从代码外观上看不出来是多棵splay。。。
makeroot
比较重要的操作,可以使任意节点成为根,这样任意树上路径都能被拉进一条链。(原本不满足深度递增是不行的。)
非常奇妙。先access(x),这时x是splay中深度最大的点,一定没有右节点了,再翻转整个splay,就是这么离谱。x就成为了深度最小的点了。
findroot
用来判断连通性,使用方法是先access再splay,最后在splay上一直向左走,最后别忘了splay(x)(保证复杂度)。
split
拉出一条(x,y) 的链。。。先makeroot(x),再access(y),最后splay(y)就可以做到访问y来访问整条链。
link
先makeroot(x),再 \(f_x = y\) ,必要时判一判findroot(y)和x是否相等,还要解释吗?
cut
如果保证断边合法,就先split(x,y)(这时根是y,且splay上只有两个点x和y,直接双向断边),记得maintain。
否则先makeroot(x),再findroot(y)。如果是x,那么就判断是否直接联通。具体方法是看y的父亲是否是x,以及y是否有左儿子(如果有,那么x~y这条边就不是直接相连的。)
splay
这个函数要被魔改一下,因为splay(x)的时候x的祖先可能还有标记没有下放,所以需要人为找到它的所有祖先,再倒序pushdown。复杂度分析参考splay即可。
pushdown
单独拿出来是想说:写代码标准化是一个好习惯。。。
因为我一直写的打标记(无论是线段树还是平衡树)是代表“被修改过,但是子节点没被修改”。
包括平衡树的区间翻转。
似乎在LCT里不这样做就会有奇怪的问题?QwQ。。。
总结:整个算法就是access排列组合,而且暴力到了嚣张的程度,但是由于基于splay,复杂度就是正确的。stotarjanorz
还有什么用FHQ写LCT的人,复杂度是错的吧,为什么还没有人出来制裁AwA。
All the last
说在最后:谢谢你读完了它!
要相信每天都会变强一点点,那么终有一天会站上峰巅。
“实力”是一个玄妙的东西,它确实和你日复一日的练习相关,但是当我问:“你是受了什么启发才做出这道题的”?
你答不上来,你甚至根本没见过类似的题目,但是你就是会做。
相信自己,也要相信魔法啊,我们所过的每个平凡的日常,也许就是连续发生的奇迹。
写代码去了。【挥手】
upd:写完了!1A了!好开心!代码贴在下面。



