Markdown-Edit mathmatical symbols and formulas

From https://www.cnblogs.com/bytesfly/p/markdown-formula.html

在用Markdown写博客时会涉及到数学符号与公式的编辑，下面进行汇总。随手记录，方便你我他。

• 行内公式：将公式插入到本行内

$0.98^{365} \approx 0.0006$

我的365天：0.98365≈0.0006${0.98}^{365}\approx 0.0006$

• 单独的公式块：将公式插入到新的一行内，并且居中

$$
1.02^{365} \approx 1377.4
$$

在座各位大佬的365天：

1.02365≈1377.4$${1.02}^{365}\approx 1377.4$$

注意：

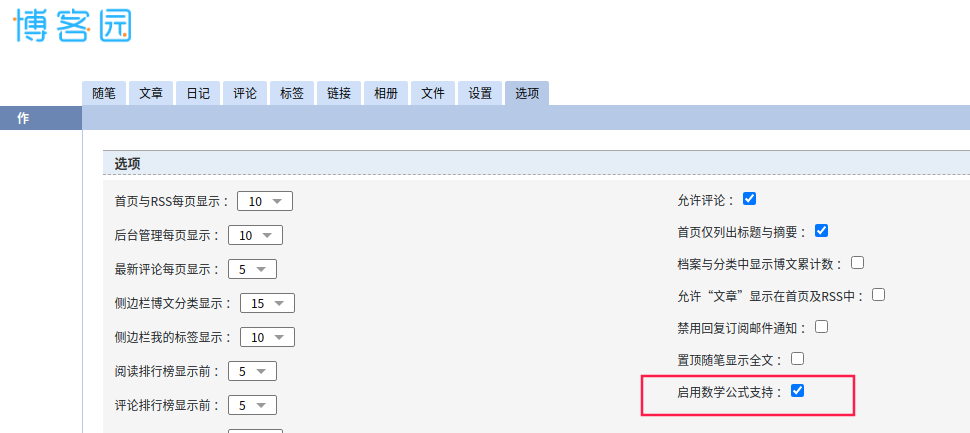
1. 在博客园用Markdown写博客需要启用数学公式支持，如下：

2. 在博客园可以在公式上右键查看详情：

   

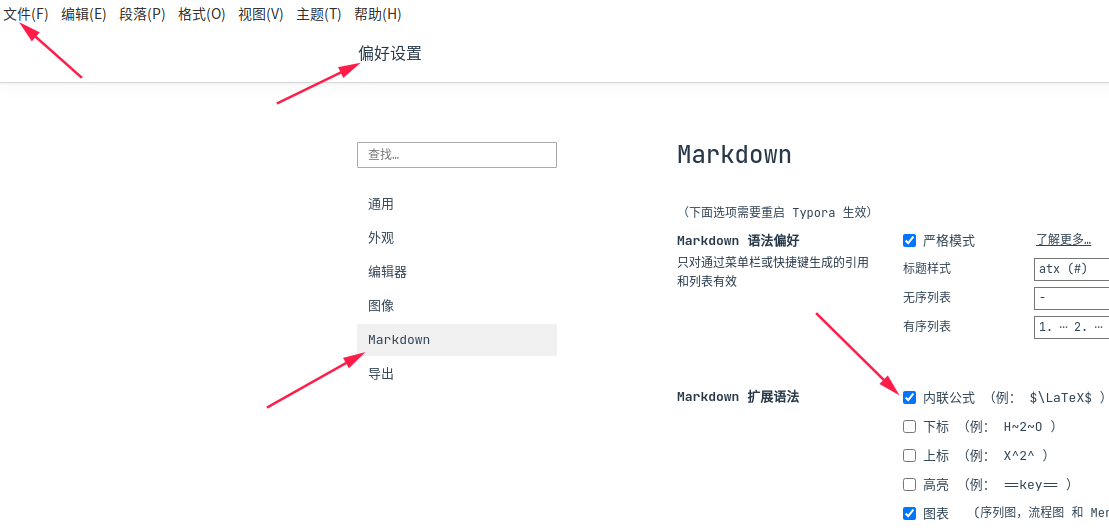
3. 如果使用Typora编写Markdown，解析行内公式需要手动设置一下， 文件 -> 偏好设置 -> Markdown -> Markdown扩展语法 -> 勾选 “内联公式”，重启软件，Typora才会解析行内公式。

符号#

上下标、运算符#

	显示效果	markdown公式语法
上标	x2、xy、e365$x^2、x^y、e^{365}$	x^2、 x^y 、e^{365}
下标	x0、a1、Ya$x_0、a_1、Y_a$	x_0、a_1、Y_a
分式	xy、1x+1$\frac{x}{y}、\frac{1}{x+1}$	\frac{x}{y}、\frac{1}{x+1}
乘	×$\times$	\times
除	÷$÷$	\div
加减	±$\pm$	\pm
减加	∓$\mp$	\mp
求和	∑$\sum$	\sum
求和上下标	∑30、∑∞0、∑∞−∞$\sum _0^3、\sum _0^{\mathrm{\infty }}、\sum _{-\mathrm{\infty }}^{\mathrm{\infty }}$	\sum_0^3 、\sum_0^{\infty} 、\sum_{-\infty}^{\infty}
求积	∏$\prod$	\prod
微分	∂$\mathrm{\partial }$	\partial
积分	∫、∫$\int 、{\displaystyle \int }$	\int 、\displaystyle\int
不等于	≠$\ne$	\neq
大于等于	≥$\ge$	\geq
小于等于	≤$\le$	\leq
约等于	≈$\approx$	\approx
不大于等于	x+y≱z$x+y\ngeqq z$	x+y \ngeq z
点乘	a⋅b$a\cdot b$	a \cdot b
星乘	a∗b$a\ast b$	a \ast b
取整函数	⌊ab⌋$\lfloor \frac{a}{b}\rfloor$	\left \lfloor \frac{a}{b} \right \rfloor
取顶函数	⌈cd⌉$\lceil \frac{c}{d}\rceil$	\left \lceil \frac{c}{d} \right \rceil

括号#

	显示效果	markdown公式语法
圆括号（小括号）	(ab)$\left(\frac{a}{b}\right)$	\left( \frac{a}{b} \right)
方括号（中括号）	[ab]$\left[\frac{a}{b}\right]$或者[xy]$[\frac{x}{y}]$	\left[ \frac{a}{b} \right]或者[ \frac{x}{y} ]
花括号（大括号）	{ab}$\{\frac{a}{b}\}$	\lbrace \frac{a}{b} \rbrace
角括号	⟨ab⟩$⟨\frac{a}{b}⟩$	\left \langle \frac{a}{b} \right \rangle
混合括号	[a,b)$[a,b)$	\left [ a,b \right )

三角函数、指数、对数#

	显示效果	markdown公式语法
sin	sin(x)$\sin (x)$	\sin(x)
cos	cos(x)$\cos (x)$	\cos(x)
tan	tan(x)$\tan (x)$	\tan(x)
cot	cot(x)$\cot (x)$	\cot(x)
log	log210${\log }_{2}10$	\log_2 10
lg	lg100$\lg 100$	\lg 100
ln	ln2$\ln 2$	\ln2

数学符号#

	显示效果	markdown公式语法
无穷	∞$\mathrm{\infty }$	\infty
矢量	a⃗ $\overrightarrow{a}$	\vec{a}
一阶导数	x˙$\dot{x}$	\dot{x}
二阶导数	x¨$\ddot{x}$	\ddot{x}
算数平均值	a¯$\overline{a}$	\bar{a}
概率分布	a^$\hat{a}$	\hat{a}
虚数i、j	ı、ȷ$ı、ȷ$	\imath、\jmath
省略号(一)	1,2,3,…,n$1,2,3,\dots ,n$	1,2,3,\ldots,n
省略号(二)	x1+x2+⋯+xn$x_1+x_2+\cdots +x_n$	x_1 + x_2 + \cdots + x_n
省略号(三)	⋮$⋮$	\vdots
省略号(四)	⋱$\ddots$	\ddots
斜线与反斜线	/ab\$/\frac{a}{b}\backslash$	\left / \frac{a}{b} \right \backslash
上下箭头	↑⏐⏐ab⏐↓⏐$\uparrow \frac{a}{b}\downarrow$	\left \uparrow \frac{a}{b} \right \downarrow
∠$\mathrm{\angle }$	∠$\mathrm{\angle }$	\angle
′$\mathrm{\prime }$	′$\mathrm{\prime }$	\prime
→$\to$	→$\to$	\rightarrow
←$\leftarrow$	←$\leftarrow$	\leftarrow
⇒$\Rightarrow$	⇒$\Rightarrow$	\Rightarrow
⇐$\Leftarrow$	⇐$\Leftarrow$	\Leftarrow
⇑$\Uparrow$	⇑$\Uparrow$	\Uparrow
⇓$\Downarrow$	⇓$\Downarrow$	\Downarrow
⟶$⟶$	⟶$⟶$	\longrightarrow
⟵$⟵$	⟵$⟵$	\longleftarrow
⟹$⟹$	⟹$⟹$	\Longrightarrow
⟸$⟸$	⟸$⟸$	\Longleftarrow
∇$\mathrm{\nabla }$	∇$\mathrm{\nabla }$	\nabla
∵$\because$	∵$\because$	\because
∴$\therefore$	∴$\therefore$	\therefore
∣$\mid$	∣$\mid$	\mid
∖$\mathrm{\setminus }$	∖$\mathrm{\setminus }$	\backslash
∀$\mathrm{\forall }$	∀$\mathrm{\forall }$	\forall
∃$\mathrm{\exists }$	∃$\mathrm{\exists }$	\exists
∽$\backsim$	∽$\backsim$	\backsim
≅$\cong$	≅$\cong$	\cong
∮$\text{∮}$	∮$\text{∮}$	\oint
⟹$⟹$	⟹$⟹$	\implies
⟺$⟺$	⟺$⟺$	\iff
⟸$⟸$	⟸$⟸$	\impliedby

连线符号#

显示效果	markdown公式语法
a+b+c←−−−−−−$\overleftarrow{a+b+c}$	\overleftarrow{a+b+c}
a+b+c−→−−−−−$\overrightarrow{a+b+c}$	\overrightarrow{a+b+c}
a+b+c←→−−−−$\overleftrightarrow{a+b+c}$	\overleftrightarrow{a+b+c}
a+b+c←−−−−−−$\underleftarrow{a+b+c}$	\underleftarrow{a+b+c}
a+b+c−→−−−−−$\underrightarrow{a+b+c}$	\underrightarrow{a+b+c}
a+b+c←→−−−−$\underleftrightarrow{a+b+c}$	\underleftrightarrow{a+b+c}
a+b+c¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯$\overline{a+b+c}$	\overline{a+b+c}
a+b+c–––––––––$\underset{\_}{a+b+c}$	\underline{a+b+c}
a+b+cSample$\stackrel{Sample}{\overbrace{a+b+c}}$	\overbrace{a+b+c}^{Sample}
a+b+cSample$\underset{Sample}{\underbrace{a+b+c}}$	\underbrace{a+b+c}_{Sample}
a+b+c1.02.0$\stackrel{2.0}{\overbrace{a+\underset{1.0}{\underbrace{b+c}}}}$	\overbrace{a+\underbrace{b+c}_{1.0}}^{2.0}
a⋅a⋯ab times$\underset{b\text{ times}}{\underbrace{a\cdot a\cdots a}}$	\underbrace{a\cdot a\cdots a}_{b\text{ times}}

高级运算符#

	显示效果	markdown公式语法
平均数运算	xyz¯¯¯¯¯¯¯¯$\overline{xyz}$	\overline{xyz}
开二次方运算	xy−−√$\sqrt{xy}$	\sqrt {xy}
开方运算	x−−√n$\sqrt[n]{x}$	\sqrt[n]{x}
极限运算(一)	limx→∞y→0xy$\underset{y\to 0}{\overset{x\to \mathrm{\infty }}{lim}}\frac{x}{y}$	\lim^{x \to \infty}_{y \to 0}{\frac{x}{y}}
极限运算(二)	limy→0x→∞xy${\displaystyle \underset{y\to 0}{\overset{x\to \mathrm{\infty }}{lim}}\frac{x}{y}}$	\displaystyle \lim^{x \to \infty}_{y \to 0}{\frac{x}{y}}
求和运算(一)	∑x→∞y→0xy$\sum _{y\to 0}^{x\to \mathrm{\infty }}\frac{x}{y}$	\sum^{x \to \infty}_{y \to 0}{\frac{x}{y}}
求和运算(二)	∑y→0x→∞xy${\displaystyle \sum _{y\to 0}^{x\to \mathrm{\infty }}\frac{x}{y}}$	\displaystyle \sum^{x \to \infty}_{y \to 0}{\frac{x}{y}}
积分运算(一)	∫∞0xdx${\int }_0^{\mathrm{\infty }}xdx$	\int^{\infty}_{0}{xdx}
积分运算(二)	∫∞0xdx${\displaystyle {\int }_0^{\mathrm{\infty }}xdx}$	\displaystyle \int^{\infty}_{0}{xdx}
微分运算	∂x∂y、∂2x∂y2$\frac{\mathrm{\partial }x}{\mathrm{\partial }y}、\frac{{\mathrm{\partial }}^{2}x}{\mathrm{\partial }{y}^2}$	\frac{\partial x}{\partial y}、\frac{\partial^2x}{\partial y^2}

集合运算#

	显示效果	markdown公式语法
属于	A∈B$A\in B$	A \in B
不属于	A∉B$A\notin B$	A \notin B
子集	x⊂y、y⊃x$x\subset y、y\supset x$	x \subset y、y \supset x
真子集	x⊆y、y⊇x$x\subseteq y、y\supseteq x$	x \subseteq y、y \supseteq x
并集	A∪B$A\cup B$	A \cup B
交集	A∩B$A\cap B$	A \cap B
差集	A∖B$A\setminus B$	A \setminus B
同或	A⨀B$A⨀B$	A \bigodot B
同与	A⨂B$A⨂B$	A \bigotimes B
异或	A⨁B$A⨁B$	A \bigoplus B
实数集合	R$\mathbb{R}$	\mathbb{R}
自然数集合	Z$\mathbb{Z}$	\mathbb{Z}

希腊字母#

大写字母	markdown语法	小写字母	markdown语法	中文注音
A$A$	A	α$\alpha$	\alpha	阿尔法
B$B$	B	β$\beta$	\beta	贝塔
Γ$\mathrm{\Gamma }$	\Gamma	γ$\gamma$	\gamma	伽马
Δ$\mathrm{\Delta }$	\Delta	δ$\delta$	\delta	德尔塔
E$E$	E	ϵ$ϵ$	\epsilon	伊普西龙
Z$Z$	Z	ζ$\zeta$	\zeta	截塔
H$H$	H	η$\eta$	\eta	艾塔
Θ$\mathrm{\Theta }$	\Theta	θ$\theta$	\theta	西塔
I$I$	I	ι$\iota$	\iota	约塔
K$K$	K	κ$\kappa$	\kappa	卡帕
Λ$\mathrm{\Lambda }$	\Lambda	λ$\lambda$	\lambda	兰布达
M$M$	M	μ$\mu$	\mu	缪
N$N$	N	ν$\nu$	\nu	纽
Ξ$\mathrm{\Xi }$	\Xi	ξ$\xi$	\xi	克西
O$O$	O	ο$o$	\omicron	奥密克戎
Π$\mathrm{\Pi }$	\Pi	π$\pi$	\pi	派
P$P$	P	ρ$\rho$	\rho	肉
Σ$\mathrm{\Sigma }$	\Sigma	σ$\sigma$	\sigma	西格马
T$T$	T	τ$\tau$	\tau	套
Υ$\mathrm{{\rm Y}}$	\Upsilon	υ$\upsilon$	\upsilon	宇普西龙
Φ$\mathrm{\Phi }$	\Phi	ϕ$\varphi$	\phi	佛爱
X$X$	X	χ$\chi$	\chi	西
Ψ$\mathrm{\Psi }$	\Psi	ψ$\psi$	\psi	普西
Ω$\mathrm{\Omega }$	\Omega	ω$\omega$	\omega	欧米伽

字体转换#

若要对公式的某一部分字符进行字体转换，可以用 {\font {需转换的部分字符}} 命令，其中\font部分可以参照下表选择合适的字体。一般情况下，公式默认为意大利体。

字体	显示效果	markdown语法
罗马体	D$\mathrm{D}$	\rm D
花体	D$\mathcal{D}$	\cal D
意大利体	D$\mathit{D}$	\it D
黑板粗体	D$\mathbb{D}$	\Bbb D
粗体	D$\mathbf{D}$	\bf D
数学斜体	D$D$	\mit D
等线体	D$\mathsf{D}$	\sf D
手写体	D$\mathcal{D}$	\scr D
打字机体	D$\mathtt{D}$	\tt D
旧德式字体	D$\mathfrak{D}$	\frak D
黑体	D$\mathit{D}$	\boldsymbol D

公式#

基本函数公式#

• 行内公式：Γ(z)=∫∞0tz−1e−tdt$\mathrm{\Gamma }(z)={\int }_0^{\mathrm{\infty }}{t}^{z-1}{e}^{-t}dt$

$\Gamma(z) = \int_0^\infty t^{z-1}e^{-t}dt$

• 行间公式：

Γ(z)=∫∞0tz−1e−tdt$$\mathrm{\Gamma }(z)={\int }_0^{\mathrm{\infty }}{t}^{z-1}{e}^{-t}dt$$

$$
\Gamma(z) = \int_0^\infty t^{z-1}e^{-t}dt
$$

• yk=φ(uk+vk)$y_k=\phi (u_k+v_k)$

$y_k=\varphi(u_k+v_k)$

• y(x)=x3+2x2+x+1$y(x)=x^3+2x^2+x+1$

$y(x)=x^3+2x^2+x+1$

• xy=(1+ex)−2xy$x^y=(1+{\mathrm{e}}^x{)}^{-2xy}$

$x^{y}=(1+{\rm e}^x)^{-2xy}$

• f(n)=∑i=1nn∗(n+1)${\displaystyle f(n)=\sum _{i=1}^{n}n\ast (n+1)}$

$\displaystyle f(n)=\sum_{i=1}^{n}{n*(n+1)}$

分段函数#

• 分段函数：

y={2x+1,x,x≤0x>0$$y=\{\begin{array}{ll}2x+1,& x\le 0\\ x,& x>0\end{array}$$

$$
y=\begin{cases}
2x+1, & x \leq0\\
x, & x>0
\end{cases}
$$

• 方程组：

⎧⎩⎨⎪⎪a1x+b1y+c1z=d1a2x+b2y+c2z=d2a3x+b3y+c3z=d3$$\{\begin{array}{c}{a}_{1}x+b_{1}y+c_{1}z=d_1\\ a_{2}x+b_{2}y+c_{2}z=d_2\\ a_{3}x+b_{3}y+c_{3}z=d_3\end{array}$$

$$
\left \{ 
\begin{array}{c}
a_1x+b_1y+c_1z=d_1 \\ 
a_2x+b_2y+c_2z=d_2 \\ 
a_3x+b_3y+c_3z=d_3
\end{array}
\right.
$$

积分#

• 积分书写：

∫θ2(x)θ1(x)=l$${\int }_{{\theta }_1(x)}^{{\theta }_2(x)}=l$$

$$
\int_{\theta_1(x)}^{\theta_2(x)}=l
$$

• 二重积分：

∬dxdy=σ$$\iint dxdy=\sigma$$

$$
\iint dx dy=\sigma
$$

• 三重积分：

∭dxdydz=ν$$\iiint dxdydz=\nu$$

$$
\iiint dx dydz=\nu
$$

微分和偏微分#

• 一阶微分方程：

dydx+P(x)y=Q(x)$$\frac{dy}{dx}+P(x)y=Q(x)$$

$$
\frac{dy}{dx}+P(x)y=Q(x)
$$

dydx∣∣∣x=0=3x+1=1$${\frac{\mathrm{d}y}{\mathrm{d}x}|}_{x=0}=3x+1=1$$

$$
\left. \frac{{\rm d}y}{{\rm d}x} \right|_{x=0}=3x+1=1
$$

• 二阶微分方程：

y′′+py′+qy=f(x)$$y^{″}+p{y}^{\prime }+qy=f(x)$$

$$
y''+py'+qy=f(x)
$$

d2ydx2+pdydx+qy=f(x)$$\frac{d^{2}y}{d{x}^2}+p\frac{dy}{dx}+qy=f(x)$$

$$
\frac{d^2y}{dx^2}+p\frac{dy}{dx}+qy=f(x)
$$

• 偏微分方程：

∂u∂t=h2(∂2u∂x2+∂2u∂y2+∂2u∂z2)$$\frac{\mathrm{\partial }u}{\mathrm{\partial }t}=h^2(\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}+\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{z}^2})$$

$$
\frac{\partial u}{\partial t}= h^2 \left( \frac{\partial^2 u}{\partial x^2} +\frac{\partial^2 u}{\partial y^2}+ \frac{\partial^2 u}{\partial z^2}\right)
$$

矩阵和行列式#

起始标记 \begin{matrix} ,结束标记\end{matrix},每一行末尾标记\，行间元素之间以&分隔。在起始、结束标记处用下列词替换matrix。

• pmatrix ：小括号边框

(1324)$$\left(\begin{array}{cc}1& 2\\ 3& 4\end{array}\right)$$

$$
\begin{pmatrix}
1&2\\
3&4\\
\end{pmatrix}
$$

• bmatrix ：中括号边框

[1324]$$\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]$$

$$
\begin{bmatrix}
1&2\\
3&4\\
\end{bmatrix}
$$

• Bmatrix ：大括号边框

{1324}$$\left\{\begin{array}{cc}1& 2\\ 3& 4\end{array}\right\}$$

$$
\begin{Bmatrix}
1&2\\
3&4\\
\end{Bmatrix}
$$

• vmatrix ：单竖线边框

∣∣∣1324∣∣∣$$\left|\begin{array}{cc}1& 2\\ 3& 4\end{array}\right|$$

$$
\begin{vmatrix}
1&2\\
3&4\\
\end{vmatrix}
$$

• Vmatrix ：双竖线边框

∥∥∥1324∥∥∥$$\Vert \begin{array}{cc}1& 2\\ 3& 4\end{array}\Vert$$

$$
\begin{Vmatrix}
1&2\\
3&4\\
\end{Vmatrix}
$$

• 无框矩阵：

111xyzx2y2z2$$\begin{array}{ccc}1& x& x^2\\ 1& y& y^2\\ 1& z& z^2\end{array}$$

$$
\begin{matrix}
    1 & x & x^2 \\
    1 & y & y^2 \\
    1 & z & z^2 \\
\end{matrix}
$$

• 单位矩阵：

⎡⎣⎢100010001⎤⎦⎥$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

$$
\begin{bmatrix}
1&0&0\\
0&1&0\\
0&0&1\\
\end{bmatrix}
$$

• m×n$m\times n$矩阵：

A=⎡⎣⎢⎢⎢⎢⎢a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn⎤⎦⎥⎥⎥⎥⎥$$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]$$

$$
A=\begin{bmatrix}
{a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\
{a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\
{\vdots}&{\vdots}&{\ddots}&{\vdots}\\
{a_{m1}}&{a_{m2}}&{\cdots}&{a_{mn}}\\
\end{bmatrix}
$$

• 行列式：

D=∣∣∣∣∣∣∣a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn∣∣∣∣∣∣∣$$D=\left|\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right|$$

$$
D=\begin{vmatrix}
{a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\
{a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\
{\vdots}&{\vdots}&{\ddots}&{\vdots}\\
{a_{m1}}&{a_{m2}}&{\cdots}&{a_{mn}}\\
\end{vmatrix}
$$

• 表格：

R1R2acbbbccac$$\begin{array}{clll}& a& b& c\\ R_1& c& b& a\\ R_2& b& c& c\end{array}$$

$$
\begin{array}{c|lll}
{}&{a}&{b}&{c}\\
\hline
{R_1}&{c}&{b}&{a}\\
{R_2}&{b}&{c}&{c}\\
\end{array}
$$

• 增广矩阵：

[142536]$$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\end{array}\right]$$

$$
\left[  \begin{array}  {c c | c} 
1 & 2 & 3 \\
4 & 5 & 6 \\
\end{array}  \right]
$$

案例#

• ^表示上标, _ 表示下标。如果上下标的内容多于一个字符，需要用{}将这些内容括成一个整体。上下标可以嵌套，也可以同时使用。

xyz=(1+ex)−2xyw$$x^{y^z}=(1+{\mathrm{e}}^x{)}^{-2x{y}^w}$$

$$
x^{y^z}=(1+{\rm e}^x)^{-2xy^w}
$$

其中\rm表示字体转换，上面有过具体说明。

• ()、[]和|表示符号本身，使用 \{ \} 来表示 {}。当要显示大号的括号或分隔符时，要用 \left 和 \right 命令。

f(x,y,z)=3y2z(3+7x+51+y2)$$f(x,y,z)=3y^{2}z(3+\frac{7x+5}{1+y^2})$$

$$
f(x,y,z) = 3y^2z \left( 3+\frac{7x+5}{1+y^2} \right)
$$

• 行标的使用：在公式末尾前使用\tag{行标}来实现行标。

f⎛⎝⎜⎜⎡⎣⎢1+{x,y}(xy+yx)(u+1)+a⎤⎦⎥3/2⎞⎠⎟⎟(公式1)$$\begin{array}{}\text{(公式1)}& f\left({[\frac{1+\{x,y\}}{(\frac{x}{y}+\frac{y}{x})(u+1)}+a]}^{3/2}\right)\end{array}$$

$$
f\left(
   \left[ 
     \frac{
       1+\left\{x,y\right\}
     }{
       \left(
          \frac{x}{y}+\frac{y}{x}
       \right)
       \left(u+1\right)
     }+a
   \right]^{3/2}
\right)
\tag{公式1}
$$

• 有时要用 \left. 或 \right. 进行匹配而不显示本身。

dudx∣∣∣x=0$${\frac{\mathrm{d}u}{\mathrm{d}x}|}_{x=0}$$

$$
\left. \frac{{\rm d}u}{{\rm d}x} \right| _{x=0}
$$

• 添加注释文字 \text

f(n)={n/2,3n+1,if n is evenif n is odd$$f(n)=\{\begin{array}{ll}n/2,& \text{if }n\text{ is even}\\ 3n+1,& \text{if }n\text{ is odd}\end{array}$$

$$
f(n)= \begin{cases}
n/2, & \text {if $n$ is even} \\
3n+1, & \text{if $n$ is odd} \\
\end{cases}
$$

• 整齐且居中的方程式序列

37−−√=732−1122−−−−−−−√=732122⋅732−1732−−−−−−−−−−−√=732122−−−−√732−1732−−−−−−−√=73121−1732−−−−−−−√≈7312(1−12⋅732)(1)(2)(3)(4)(5)$$\begin{array}{}\text{(1)}& \sqrt{37}& =\sqrt{\frac{{73}^2-1}{{12}^2}}\text{(2)}& & =\sqrt{\frac{{73}^2}{{12}^2}\cdot \frac{{73}^2-1}{{73}^2}}\text{(3)}& & =\sqrt{\frac{{73}^2}{{12}^2}}\sqrt{\frac{{73}^2-1}{{73}^2}}\text{(4)}& & =\frac{73}{12}\sqrt{1-\frac{1}{{73}^2}}\text{(5)}& & \approx \frac{73}{12}(1-\frac{1}{2\cdot {73}^2})\end{array}$$

$$
\begin{align}
    \sqrt{37} & = \sqrt{\frac{73^2-1}{12^2}} \\
              & = \sqrt{\frac{73^2}{12^2}\cdot\frac{73^2-1}{73^2}} \\ 
              & = \sqrt{\frac{73^2}{12^2}}\sqrt{\frac{73^2-1}{73^2}} \\
              & = \frac{73}{12}\sqrt{1-\frac{1}{73^2}} \\ 
              & \approx \frac{73}{12}\left(1-\frac{1}{2\cdot73^2}\right) \\
\end{align}
$$

• 在一个方程式序列的每一行中注明原因

v+w−w−w+0=0=−w+0=−w+(v+w)Givenadditive identityequations (1) and (2)(1)(2)(6)$$\begin{array}{}\text{(1)}& v+w& =0& \text{Given}\text{(2)}& -w& =-w+0& \text{additive identity}\text{(6)}& -w+0& =-w+(v+w)& \text{equations }(1)\text{ and }(2)\end{array}$$

$$
\begin{align}
    v + w & = 0  & \text{Given} \tag 1 \\
       -w & = -w + 0 & \text{additive identity} \tag 2 \\
   -w + 0 & = -w + (v + w) & \text{equations $(1)$ and $(2)$} \\
\end{align}
$$

• 文字在左对齐显示

if n is even:if n is odd:n/23n+1}=f(n)$$\begin{array}{ll}\text{if }n\text{ is even:}& n/2\\ \text{if }n\text{ is odd:}& 3n+1\end{array}\}=f(n)$$

$$
    \left.
        \begin{array}{l}
            \text{if $n$ is even:} & n/2 \\
            \text{if $n$ is odd:} & 3n+1 \\
        \end{array}
    \right\}
    =f(n)
$$

• 连分式

x=a0+12a1+22a2+32a3+44a4+⋯$$x=a_0+\frac{1^2}{a_1+\frac{2^2}{a_2+\frac{3^2}{a_3+\frac{4^4}{a_4+\cdots }}}}$$

$$
x = a_0 + \cfrac{1^2}{a_1 +
            \cfrac{2^2}{a_2 +
              \cfrac{3^2}{a_3 +
                \cfrac{4^4}{a_4 + 
                  \cdots
                }
              }
            }
          }
$$

• 表格

通常，一个格式化后的表格比单纯的文字或排版后的文字更具有可读性。
数组和表格均以 \begin{array} 开头，并在其后定义列数及每一列的文本对齐属性，c l r 分别代表居中、左对齐及右对齐。若需要插入垂直分割线，在定义式中插入 | ，若要插入水平分割线，在下一行输入前插入 \hline 。
与矩阵相似，每行元素间均须要插入 & ，每行元素以 \ 结尾，最后以 \ end{array} 结束数组。

n123左对齐0.24−1−20居中对齐11892000右对齐125−81+10i$$\begin{array}{clcr}n& \text{左对齐}& \text{居中对齐}& \text{右对齐}\\ 1& 0.24& 1& 125\\ 2& -1& 189& -8\\ 3& -20& 2000& 1+10i\end{array}$$

$$
\begin{array}{c|lcr}
    n & \text{左对齐} & \text{居中对齐} & \text{右对齐} \\
    \hline
    1 & 0.24 & 1 & 125 \\
    2 & -1 & 189 & -8 \\
    3 & -20 & 2000 & 1+10i \\
\end{array}
$$