水面渲染-浮力的一种实现
在Github发现一个很有意思的项目github.com/dbrizov/Unity-WaterBuoyancy,
这个项目基于unity游戏引擎开发,为水体增加了浮力这一物理要素。尽管浮力的实现代码只有短短一百多行,但多了浮力的水面仿佛有了灵魂,这就是游戏开发技术的魅力啊。

浮力定义
那浮力是怎么实现,我们回顾下浮力的定义。
漂浮于流体(液体或气体)表面或浸没于流体之中的物体,受到各方向流体静压力的向上合力。其大小等于被物体排开流体的重力。
简单来说,浮力方向与重力相反,它的大小等于物体排开液体的重力。知道了浮力的原理,那么就很容易在水面渲染中实现它,我们只需要知道物体浸入水中的体积,水的密度,就很容易计算出浮力了。
体积的计算
物体总体积的计算
首先我们尝试计算物体的总体积,这里我们假设物体是实心的。
我们知道游戏的物体的本质是网格,而网格本质是由多个三角形面近似成的几何体
所以只需要获取物体的网格信息中的三角形面片数据,计算网格每一个三角形面片和物体中心点所构成三角锥的体积,三角锥总和便是物体的总体积
/// <summary>
/// 计算体积
/// </summary>
private void CalualateVolume()
{
MeshFilter mf = GetComponent<MeshFilter>();
Mesh mesh = mf.mesh;
float volume = 0f;
Vector3[] vertices = mesh.vertices;
int[] triangles = mesh.triangles;
for (int i = 0; i < mesh.triangles.Length; i += 3)
{
Vector3 p1 = vertices[triangles[i + 0]];
Vector3 p2 = vertices[triangles[i + 1]];
Vector3 p3 = vertices[triangles[i + 2]];
Vector3 a = p1 - p2;
Vector3 b = p1 - p3;
Vector3 c = p1 - Vector3.zero;
volume += (Vector3.Dot(a, Vector3.Cross(b, c))) / 6f;
}
m_Volume = Mathf.Abs(volume) * transform.localScale.x * transform.localScale.y * transform.localScale.z;
}
计算物体浸入水中部分的体积
物体的总体积计算成功了,那如何计算物体浸入水中的部分呢,这次我们可不能通过计算三角锥的方法来计算了,因为物体实际被水面截断了,三角锥可能存在少许浸入水中,大部分露出水面的情况。
dbrizov/Unity-WaterBuoyancy项目提出体素这个概念,它把一个物体量化成均匀分布的点,只需要计算浸入水中的点的数目,便可近似得到物体浸入水中部分的体积
获取体素列表
private void CalualateVoxels()
{
Quaternion initialRotation = this.transform.rotation;
this.transform.rotation = Quaternion.identity;
Bounds bounds = m_Bounds;
this.voxelSize.x = bounds.size.x / VoxelSize;
this.voxelSize.y = bounds.size.y / VoxelSize;
this.voxelSize.z = bounds.size.z / VoxelSize;
List<Vector3> voxels = new List<Vector3>( VoxelSize * VoxelSize * VoxelSize);
for (int j = 0; j < VoxelSize; j++)
{
for (int i = 0; i < VoxelSize; i++)
{
for (int k = 0; k < VoxelSize; k++)
{
float pX = bounds.min.x + this.voxelSize.x * (0.5f + i);
float pY = bounds.min.y + this.voxelSize.y * (0.5f + j);
float pZ = bounds.min.z + this.voxelSize.z * (0.5f + k);
Vector3 point = new Vector3(pX, pY, pZ);
if (IsPointInsideCollider(point))
{
voxels.Add(this.transform.InverseTransformPoint(point));
}
}
}
}
transform.rotation = initialRotation;
m_Voxels = voxels.ToArray();
}
private bool IsPointInsideCollider(Vector3 point)
{
float rayLength = m_Bounds.size.magnitude;
Ray ray = new Ray(point, m_Collider.transform.position - point);
RaycastHit hit;
if (Physics.Raycast(ray, out hit, rayLength))
{
if (hit.collider == m_Collider)
{
return false;
}
}
return true;
}
浮力实现1.0版
我们首先计算物体完全浸入水中所受到浮力,再平摊到每一个体素上,物体受到的总浮力便是浸入水中体素所受到浮力之和
总浮力的计算
int len = m_Voxels.Length;
float submergedVolume = 0f;
Vector3 force = water.Density * m_Volume * -Physics.gravity / m_Voxels.Length;//单个体素受到的浮力
for (int i = 0; i < len; i++)
{
Vector3 worldPoint = transform.TransformPoint(m_Voxels[i]);
float submergedFactor = 0;
if (worldPoint.y < water.transform.position.y)
{
submergedVolume += 1;
}
}
m_Rigidbody.AddForce(force * submergedVolume);
表现效果

这里已经初步实现了浮力,但胶囊几何体出现了不自然的直立,我们希望物体能和水面交互,产生旋转等效果
浮力实现2.0版
我们希望物体会自然的旋转,那么物体所受力的方向不能只是简单的垂直向上。
dbrizov/Unity-WaterBuoyancy是这样实现的
Vector3 worldPoint = transform.TransformPoint(m_Voxels[i]);
float submergedFactor = 0;
if (worldPoint.y < water.transform.position.y)
{
submergedFactor = 1;
submergedVolume += submergedFactor;
}
Vector3 surfaceNormal = water.GetSurfaceNormal(worldPoint);
Quaternion surfaceRotation = Quaternion.FromToRotation(water.transform.up, surfaceNormal);
surfaceRotation = Quaternion.Slerp(surfaceRotation, Quaternion.identity, submergedFactor);
Vector3 finalVoxelForce = surfaceRotation * force * submergedFactor;
m_Rigidbody.AddForceAtPosition(finalVoxelForce, worldPoint);
Debug.DrawLine(worldPoint, worldPoint + finalVoxelForce.normalized, Color.blue);
它把物体所受的浮力平摊到每个点上,而每个点受到的浮力方向应该是与水面法线相同,所以需要一个四元数矫正力的方向
最后的结果是这样的
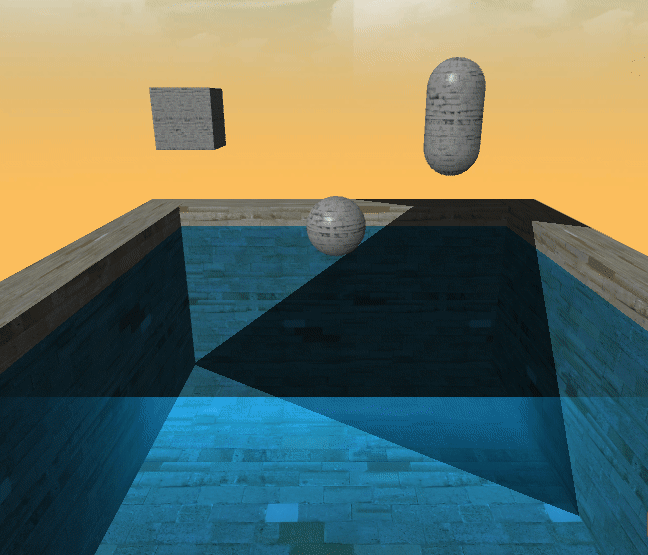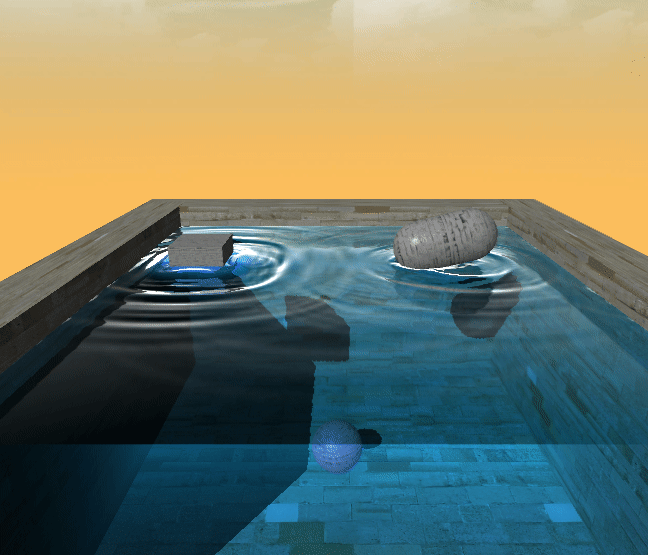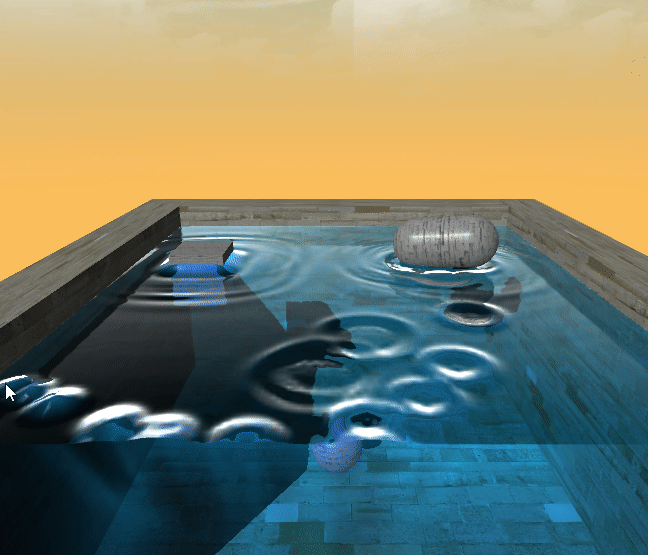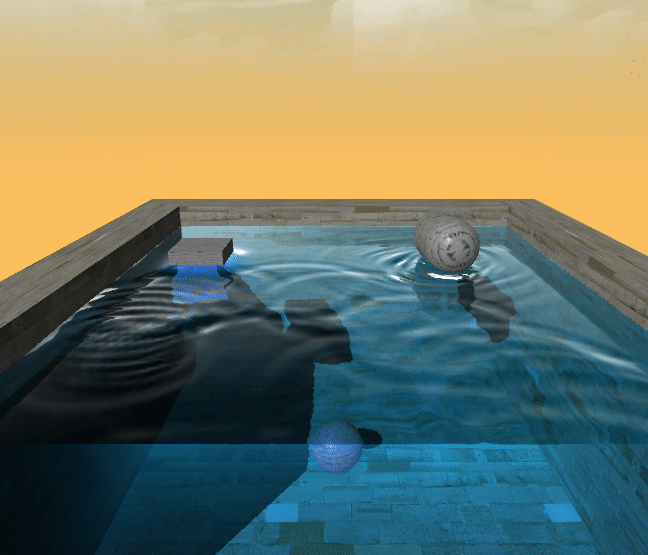



 浙公网安备 33010602011771号
浙公网安备 33010602011771号