后缀树的建立-Ukkonen算法
Ukkonen算法,以字符串abcabxabcd为例,先介绍一下运算过程,最后讨论一些我自己的理解。
需要维护以下三个变量:
- 当前扫描位置
# - 三元组
活动节点(AN),活动边(AE),活动长度(AL) - 剩余后缀数:表示还有多少个潜在后缀应该被插入还没有插入
每多扫描一个后缀,其实是增加了一个新的后缀,从#=0-2的过程可以看出。
举个例子:
ab的后缀有ab和b,可以表示成[0,],[1,]abc的后缀有abc,bc和c,可以表示成[0,],[1,]和[2,]
增加了c之后,前两个后缀事实上可以使用相同的表示法,这样只有一个新的c后缀需要被增加
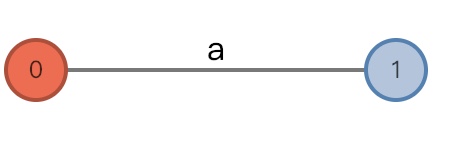
#=0, char='a'
- 增加前:
(root, "", 0), remainder = 1 - 为根节点增加一条边:
[0,],由于确实增加了条边,所以remainder会减少 - 增加后:
(root, "", 0), remainder = 0
![1]()
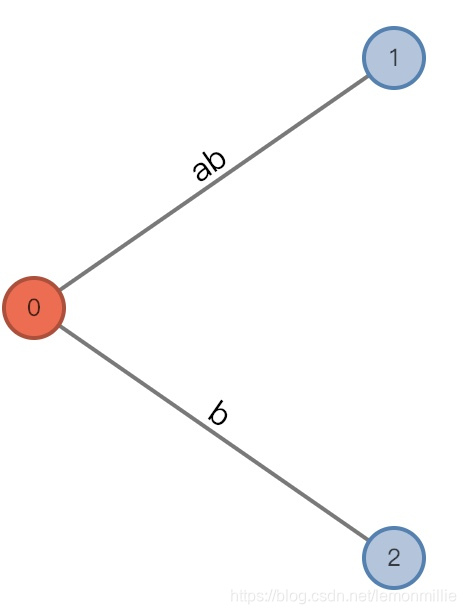
#=1, char='b'
- 增加前:
(root, "", 0), remainder = 1 - 为根节点增加一条边:
[1,],由于确实增加了条边,所以remainder会减少 - 增加后:
(root, "", 0), remainder = 0
![2]()
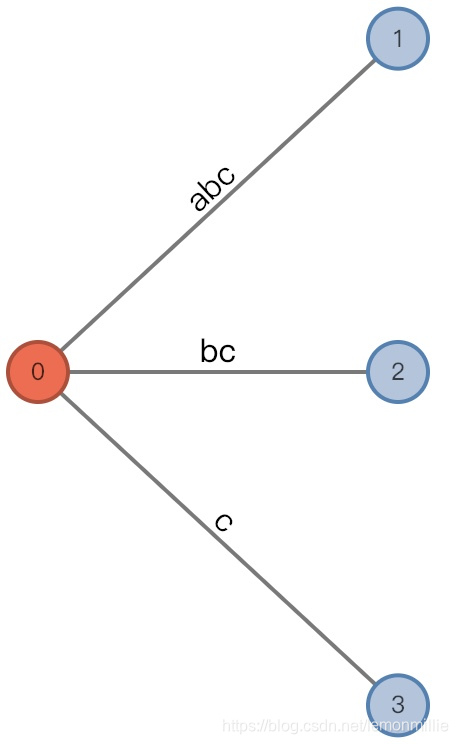
#=2, char='c'
- 增加前:
(root, "", 0), remainder = 1 - 为根节点增加一条边:
[2,],由于确实增加了条边,所以remainder会减少 - 增加后:
(root, "", 0), remainder = 0
![3]()
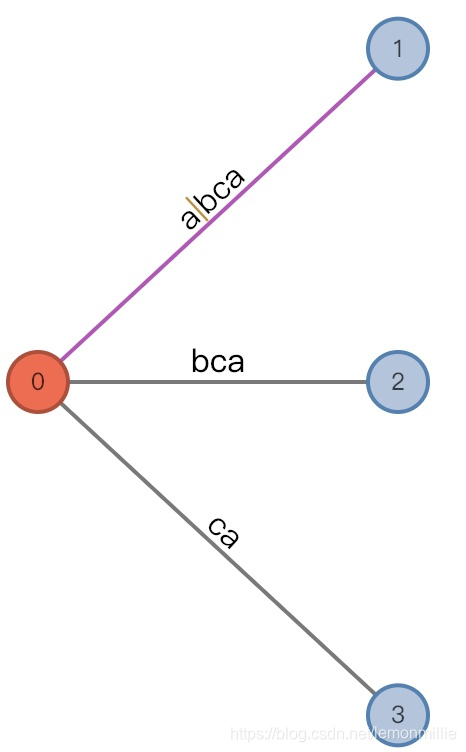
#=3, char='a'
- 增加前:
(root, "", 0), remainder = 1 - 由于新增加的后缀
a已经在根结点(活动节点)处伸了一个边出去了,所以这回不增加,只是修改三元组现在我们知道了,三元组
(AN,AE,AL)的意思是,活动边为从AN伸出的以AE开头的边的第AL个字符后。
并且由于这条边表示为[i,],所以它的总长度应为#-i+1,分界线前最后一个字符为str[i+AL-1],分界线后第一个字符为i+AL - 增加后:
(root,"a"/[0,], 1), remainder = 1
![4]()
#=4, char='b'
- 增加前:
(root,"a"/[0,], 1), remainder = 2 - 发生的事情跟上一步一样
- 增加后:
(root,"a"/[0,], 2), remainder = 2
![5]()
#=5, char='x'
-
增加前:
(root,"a"/[0,], 2), remainder = 3 -
这一步发生了复杂的事情,现在有待增加的后缀已经有3个了,分别是
abx,bx和x可以看出,有待增加的后缀为
str[#-remainder+1:#]中的remainder个后缀由于
c和x不同,之前的偷懒现在要偿还了:-
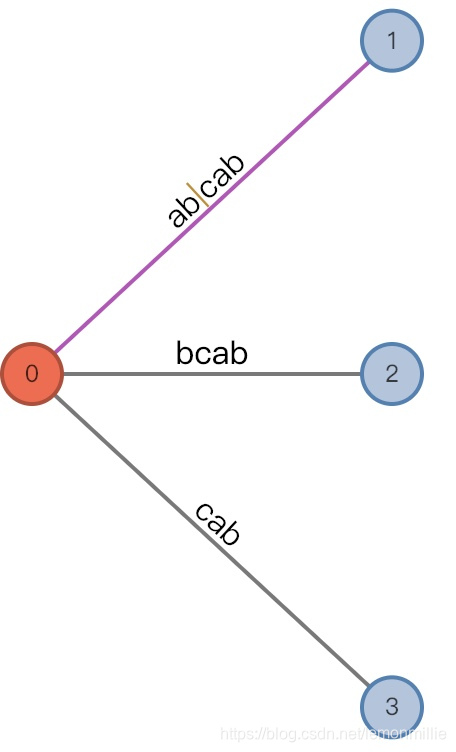
第一个添加
abx,它必然在三元组指示的地方分裂,分裂一个新节点ab【其实也可以用下标, 后面再说】,原来的叶子边修改为[2,]【显然是因为[i+AL,]】,新增加的叶子结点一定为[5,]注意这里分裂的新结点是非叶结点!!! 因为相当于竖线的地方有个隐藏节点, 把它变成真实节点了
从另一个方面想, 为什么增加非叶结点呢? 是因为要保留原来1后面的子树![6]() 由于插入了一条边,remainder减少为2
由于插入了一条边,remainder减少为2 -
然后执行向插入
bx。注意,原来三元组为(root, "a"/[0,], 2),匹配的是abx,那么显然,从root开始匹配bx的话,会从[1,]开始匹配,AL也减少一位。所以,插入b的时候三元组变成(root,"b"/[1, ], 1)(如上图)
插入x的时候新增中间节点"b",原来的[1,]变成[2,],新增叶子节点[5,]
![7]()
这里有一个新的规则:
在#相等的同一次扫描里,分裂的结点之间要有链接,由先分裂的指向后分裂的,如图 -
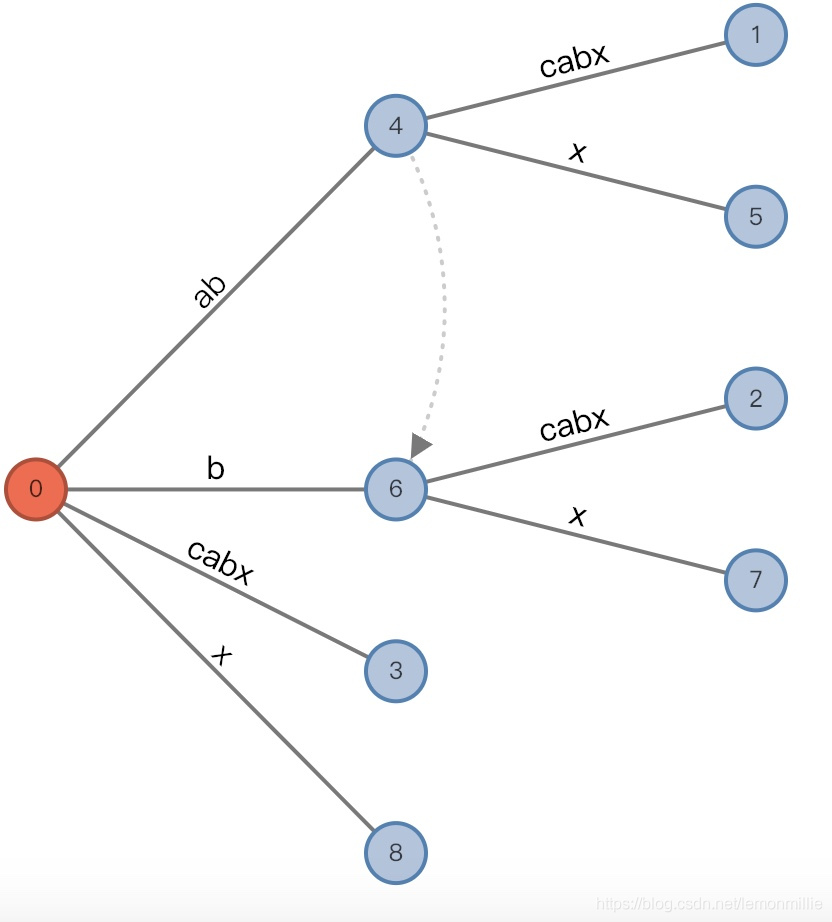
现在remainder减少为1,因为
c和x不匹配,从root开始匹配x是找不到合适的边的,所以没办法将三元组变成(root,"c"/[2, ], 0),而既然活动长度为0了,三元组还是回到初始的(root,"", 0)状态,在这个状态下插入x,将直接插入新边[5,]
-
-
增加后:
(root,"", 0), remainder = 0
![8]()
#=6, char='a'
- 增加前:
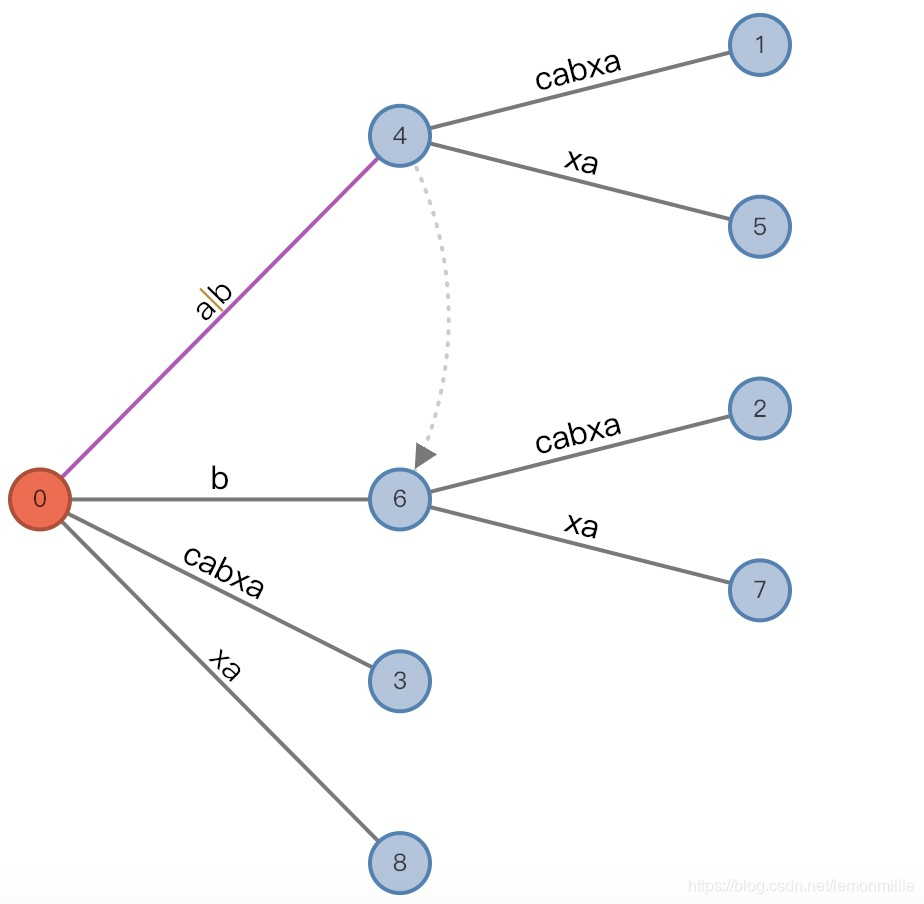
(root,"", 0), remainder = 1 - 发生的事情与
#=3时相似 - 增加后:
(root,"a"/"ab", 1), remainder = 1
![9]()
#=7, char='b'
- 增加前:
(root,"a"/"ab", 1), remainder = 2 - 发生的事情与
#=4时相似,不过这个时候我们发现中间结点"ab"已经遍历完成了,emmm那就要发生活动节点的转移:
(4,"", 0), remainder = 2 - 增加后:
(4,"", 0), remainder = 2
![10]()
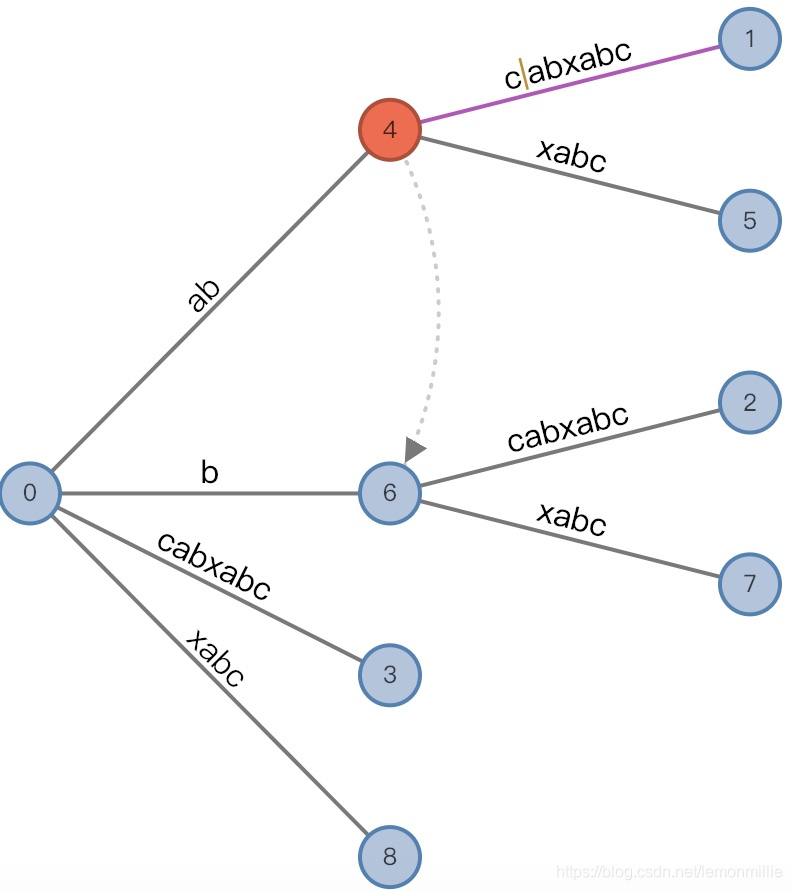
#=8, char='c'
- 增加前:
(4,"", 0), remainder = 3 - 推迟后缀的插入
- 增加后:
(4,"c"/[2,], 1), remainder = 3
![11]()
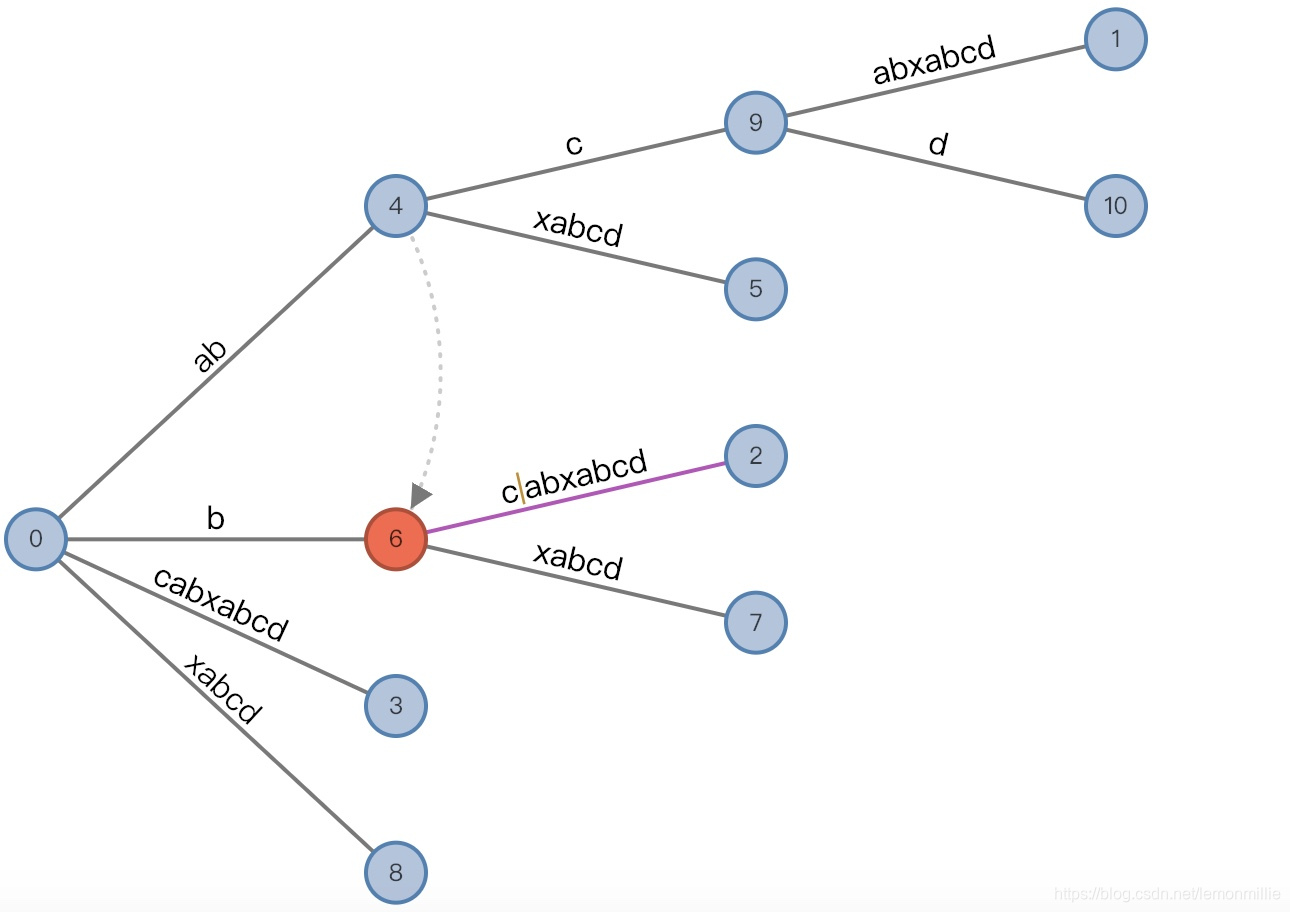
#=9, char='d'
- 增加前:
(4,"c"/[2,], 1), remainder = 4 - 这里发生的事情也很复杂:
-
首先按照之前说的,分裂活动节点
4,得到中间节点"c"和两个叶子节点[3,],[9,]。
![12]()
-
按照我们之前学习的规则,本来是要把状态改成:
(4,"", 0), remainder = 3然后再向活动节点4增加新后缀bcd的。
但是4不是根节点,所以它适用于一条新规则:向
(AN,AE,AL)添加完后缀,还要再添加新后缀时,如果节点不是根节点,则要将活动节点转移到链接的下一个节点(设为AN’,如果没有下一个节点,那就转移到root),并保持AE和AL不变。
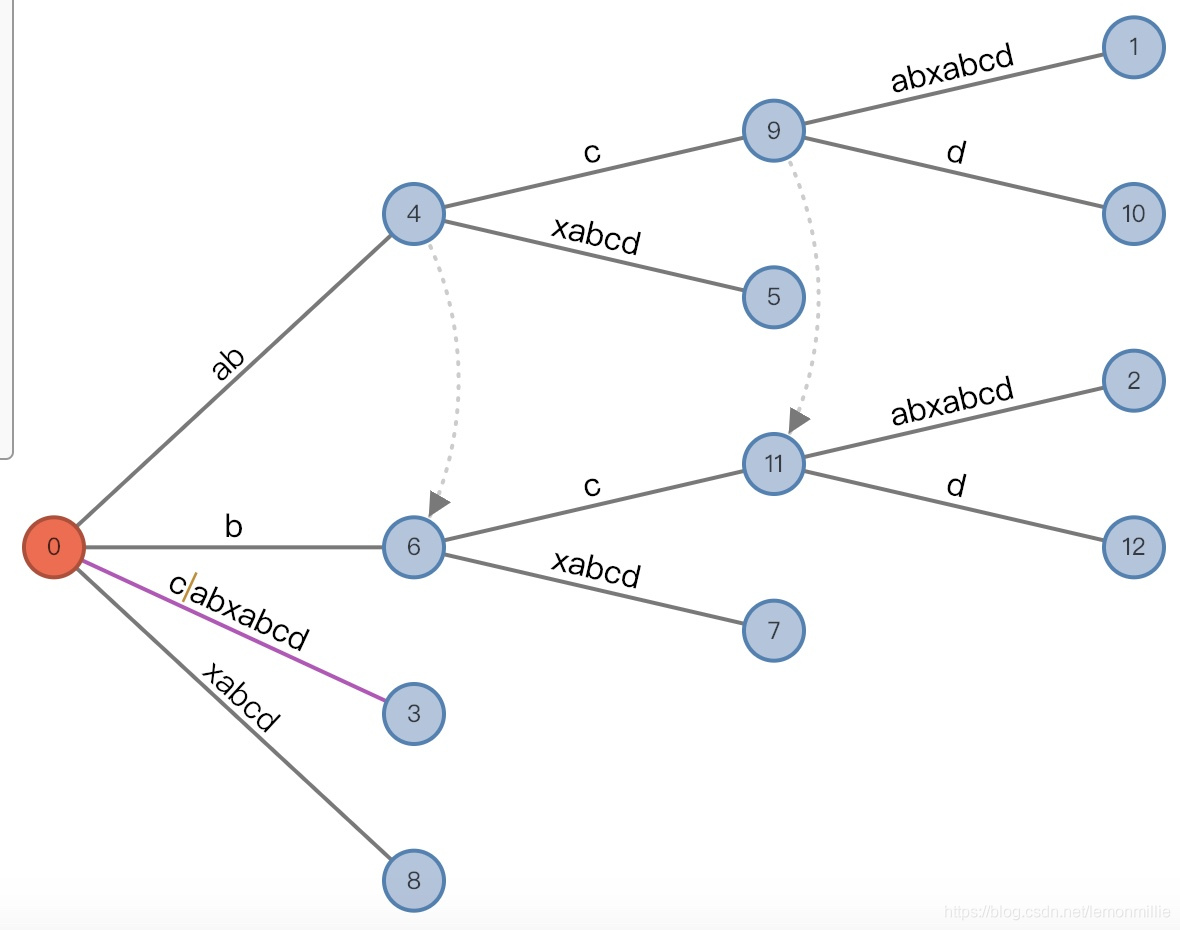
这是因为下一个节点和这个节点有相同的边,所以AE和AL都不需要改变! 后面我们详细讨论这个链接所以状态变成
(6,"c"/[2,], 1), remainder = 3,然后再分裂,得到如图状态:
![13]()
和(root,"c"/[2,], 1), remainder = 2,同时,由于发生了连续分裂,需要记录链接 -
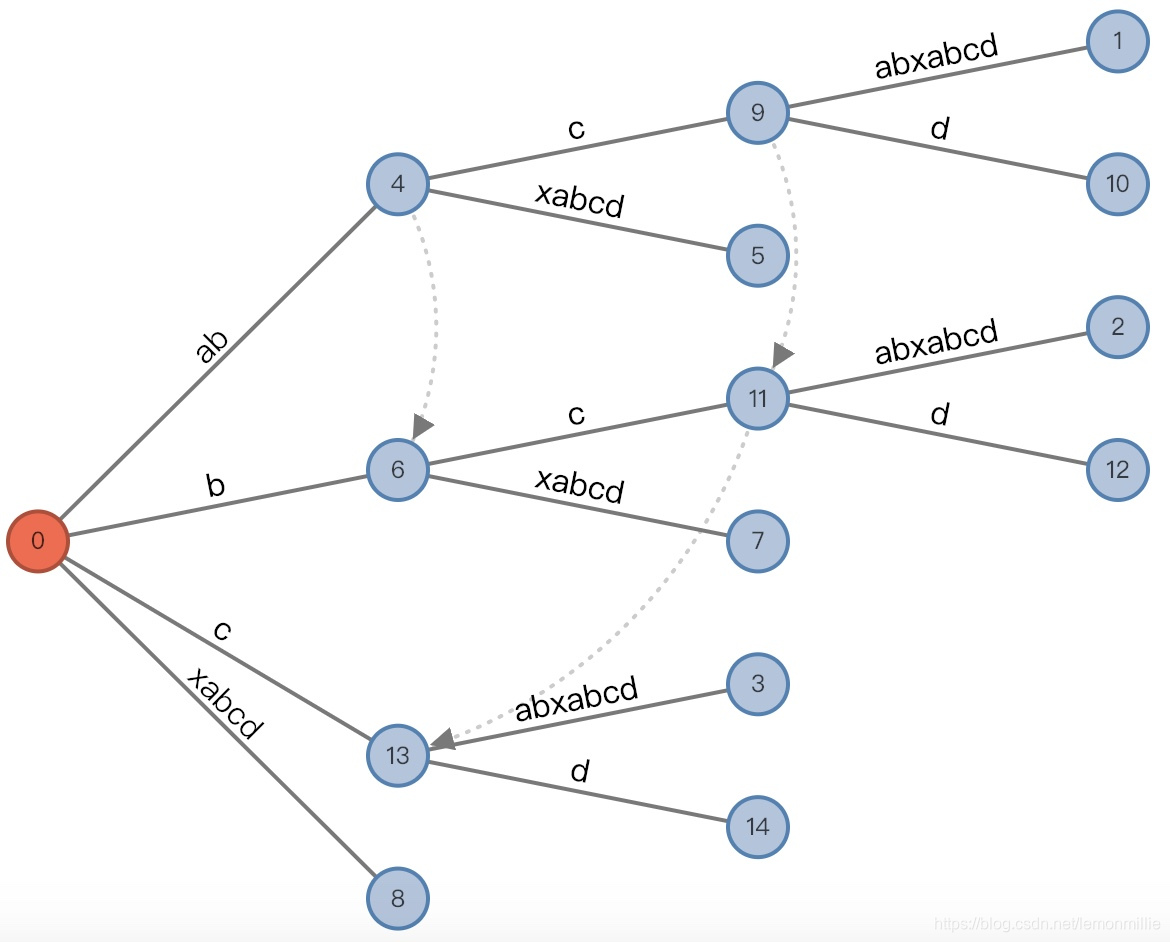
接下来的事情不用说了:
![14]()
(root,"", 0), remainder = 1,记录链接 -
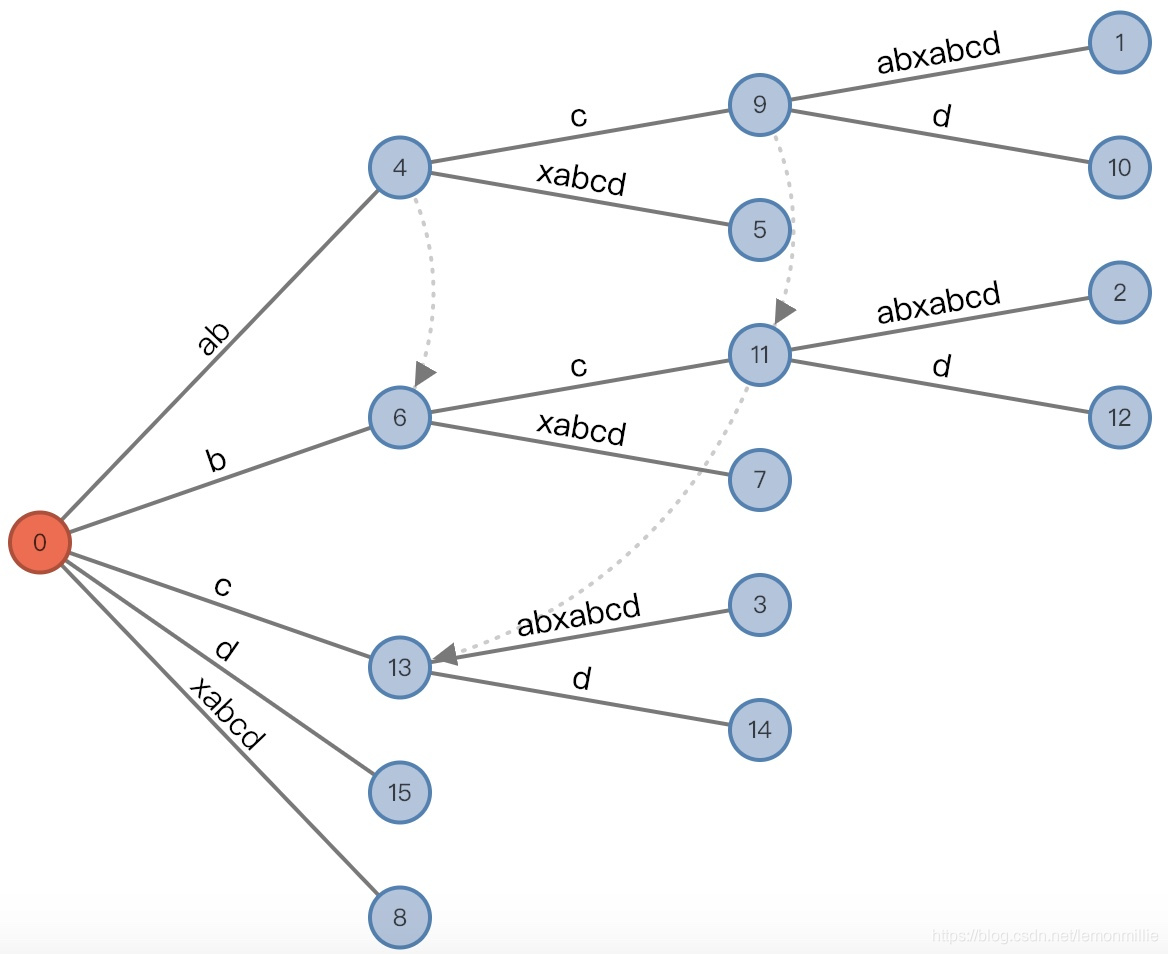
最后再添加后缀
d
-
- 增加后:
(root,"", 0), remainder = 0
![15]()
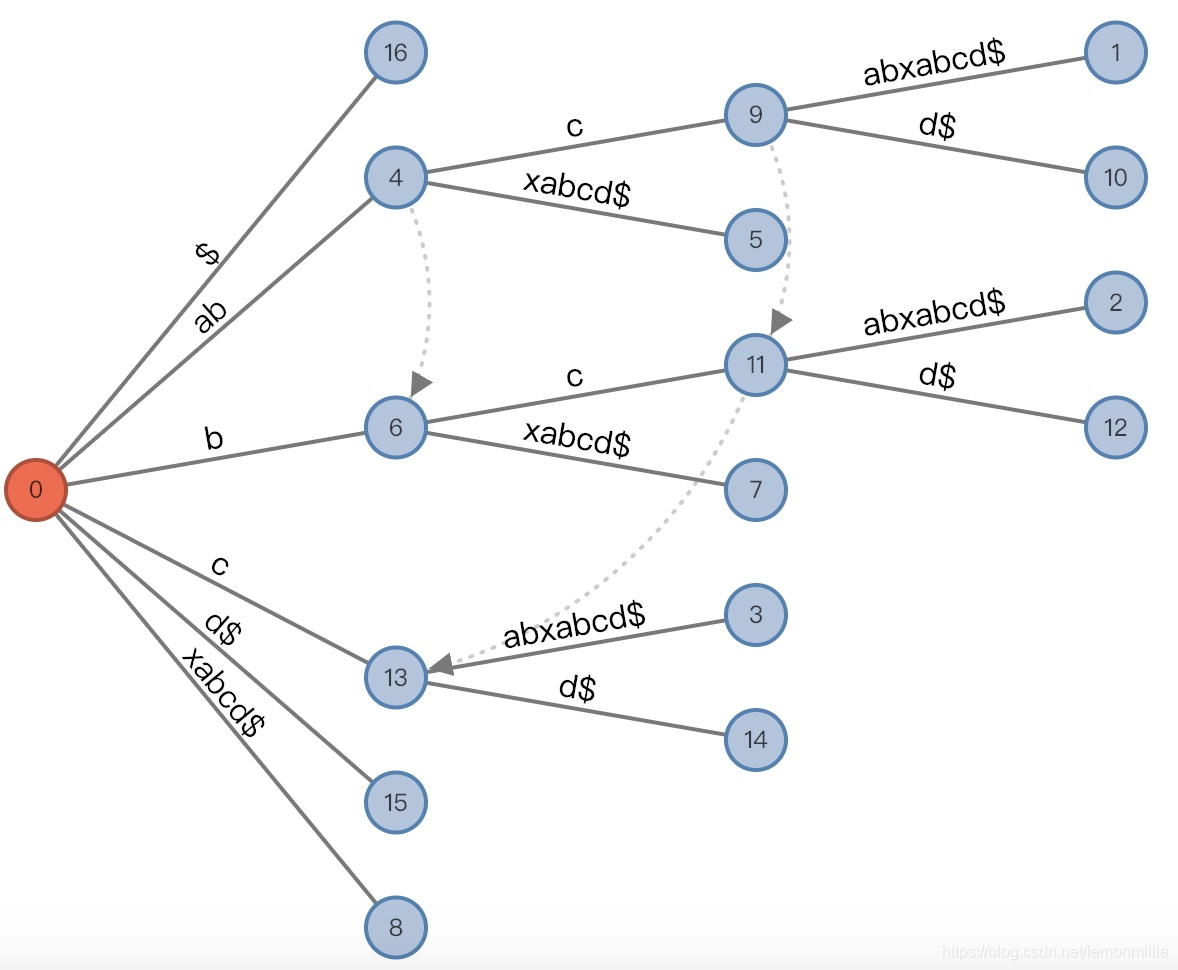
#=10, char='$'
最后还要假设添加一个虚拟结尾$,这是因为假如结束的时候remainer不为0,有一些后缀被隐藏在了活动节点里,这样得到的后缀树是隐式后缀树,不好用,我们需要保证后缀一定结束在叶子节点。
- 增加前:
(root,"", 0), remainder = 1 - root加了一个新边
- 增加后:
(root,"", 0), remainder = 0
![16]()
总结
而另一方面,竖线的位置又可以通过AL来计算,前面我们说过了,是i+AL。
此外,由于相等关系,还有一个等式:
总之结论就是,在中间节点通过下标来记录的时候,这些相等关系可以减少我们需要保持的变量,实际使用的过程中根据自己代码的不同考虑清楚它们之间的关系即可。
链接的意义
从上面的图示明显可以看出,链接到一起的节点都伸出了相同的边,而分裂都发生在这些边上。
这是因为,某个位置#处发生的分裂都一定产生一条[#,]的边,所以链接到一起的节点一定有相同的边。
所以链接是为了快速地找到下一个分裂的节点,而不需要再从头开始匹配。
链接的最后一定是root,因为root一定存过所有的边
整理代码
状态变量:(AN,AL)
AE也不需要存,用#和AL返推出AE的首字母再从AN里查就可以了
树结构需求
-
叶子结点:
begin -
非叶子节点:
beginend- 边列表,按首字母存
- 链接
-
根结点:
- 边列表,按首字母存
综上,树节点可以定义为:
class SuffixNode(object):
def __init__(index, end=None, suffix=None):
self.begin = index
self.end = end
self.edge = {}
self.suffix = suffix
广义后缀树建立代码
写了一个,还没用题目测试过
class SuffixTree(object):
class SuffixTreeNode(object):
def __init__(self, index, end=None, suffix=None, isleaf = True):
self.begin = index
self.end = end
self.edge = {}
self.suffix = suffix
def __init__(self):
self.al = 0
self.s = ""
self.now = self.SuffixTreeNode(-1)
self.root = self.now
self.words = []
def add(self, string):
beg = len(self.s)
self.s += string+'$'
self.words.append(len(self.s))
end = len(self.s)
for ptr in xrange(beg,len(self.s)):
char = self.s[ptr]
self.al += 1 # 多一个等待存的后缀
last = None
while self.al:
ae = self.s[ptr - self.al+1]
if ae in self.now.edge:
# 有边, 开始匹配字符
sc = self.s[self.now.edge[ae].begin + self.al-1]
if sc == char:
# 如果匹配, 不增加边
# 如果有前驱节点, 存链接
if last!=None:
last.suffix = self.now
last = self.now
# 匹配满的时候转移活动节点
if self.al >= self.now.edge[ae].end-self.now.edge[ae].begin:
self.now = self.now.edge[ae]
self.al -= (self.now.end-self.now.begin)
break # 如果隐含了, 就不再分裂, 直接往下一个位置走
else:
# 如果不匹配, 开始分裂
new = self.SuffixTreeNode(self.now.edge[ae].begin, self.now.edge[ae].begin + self.al -1, self.root, False)
self.now.edge[ae].begin = self.now.edge[ae].begin + self.al -1
new.edge[char] = self.SuffixTreeNode(ptr, end)
new.edge[sc] = self.now.edge[ae]
self.now.edge[ae] = new
# 如果有前驱节点, 存链接
if last != None:
last.suffix = new # 因为new添加了新叶子节点
last = new
else:
# 没边, 添加一个新边
self.now.edge[ae] = self.SuffixTreeNode(ptr, end)
# 如果有前驱节点, 存链接
if last != None:
last.suffix = self.now # 因为new添加了新叶子节点
last = self.now
if self.now.begin != -1:
self.now = self.now.suffix
# 活动长度不用变
else:
self.al -= 1
 由于插入了一条边,remainder减少为2
由于插入了一条边,remainder减少为2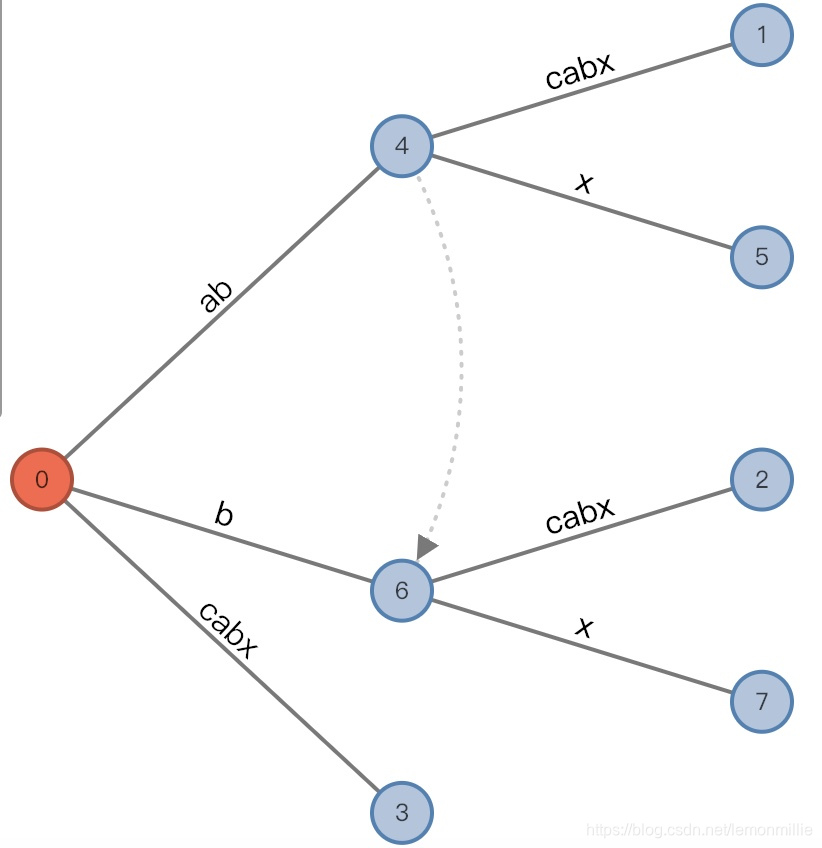


 浙公网安备 33010602011771号
浙公网安备 33010602011771号