利用编译原理来解决表达式分析、注释分析、表达式转换等题

写这篇是做LC 770的时候受到了，参考评论区@mbinary 的答案的启发。
编译原理学了不能白学吧，遇到这类题目可以根据编原有一套方法论，而不是自己在那瞎递归瞎调试，又慢又容易出错
像很多表达式分析等题，括号是嵌套的，这种是没办法只用正则解决的，需要通过语法分析来搞定。

词法分析

直接复制课件叭
1

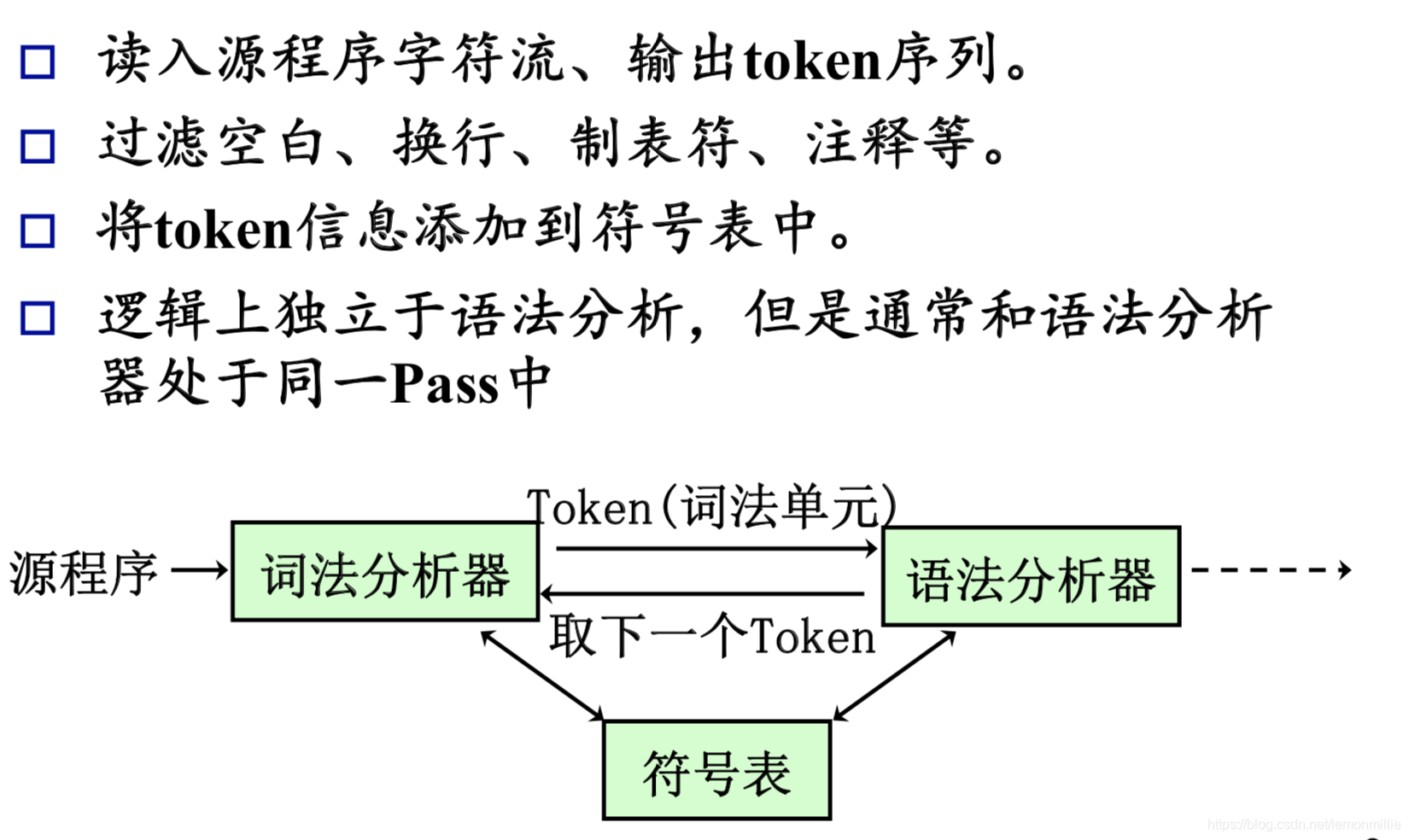
词法自动识别过程

2
以LC 770为例，参考评论区@mbinary 的答案
所有的token包括：

  • num：数字，由0-9数字构成，由于题目不会给出非法数字，故为[0-9]+
  • var：变量，由小写字母构成，故为[a-z]+
  • +：加号
  • -：减号
  • *：乘号
  • `(’：左括号
  • )：右括号

结合下文语法分析看，token就是语法分析里说的“终结符号集合”

匹配过程中需要解决的问题

3

语法分析

句子的语法

4
以LC 770为例，参考评论区@mbinary 的答案

  • VT=num,var,’+’,’-’,’*’,’(’,’)’V_T=\text{{num,var,'+','-','*','(',')'}}
  • VN=expr, term, itemV_N=\text{{expr, term, item}}
  • S=初始表达式S=\text{初始表达式}
  • P=P=
    expr -> expr {'+'|'-'} term | term
term -> term '*' item | item
item -> num | var | '(' expr ')'

终结符号就是token，非终结符号就是规则里的其它符号。
一般P确定了符号集就确定了，而P里一定至少有一条以S为开头的，约定把S开头的规则写在最前面，这样S也确定了。
5
比如：
6

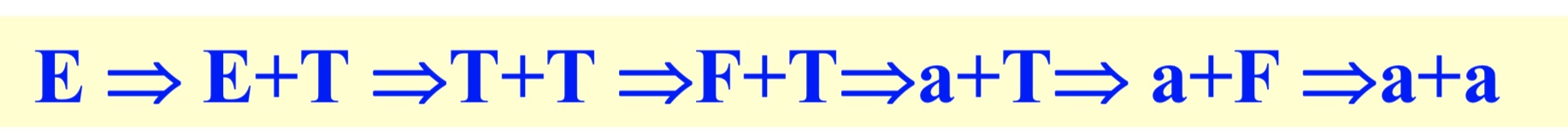
上下文无关文法： 规则集全是【A→βA\rightarrow\beta】而不是【AB→βAB\rightarrow\beta或者BA→βBA\rightarrow\beta】，前者不需要知道上下文

语法分析树

7
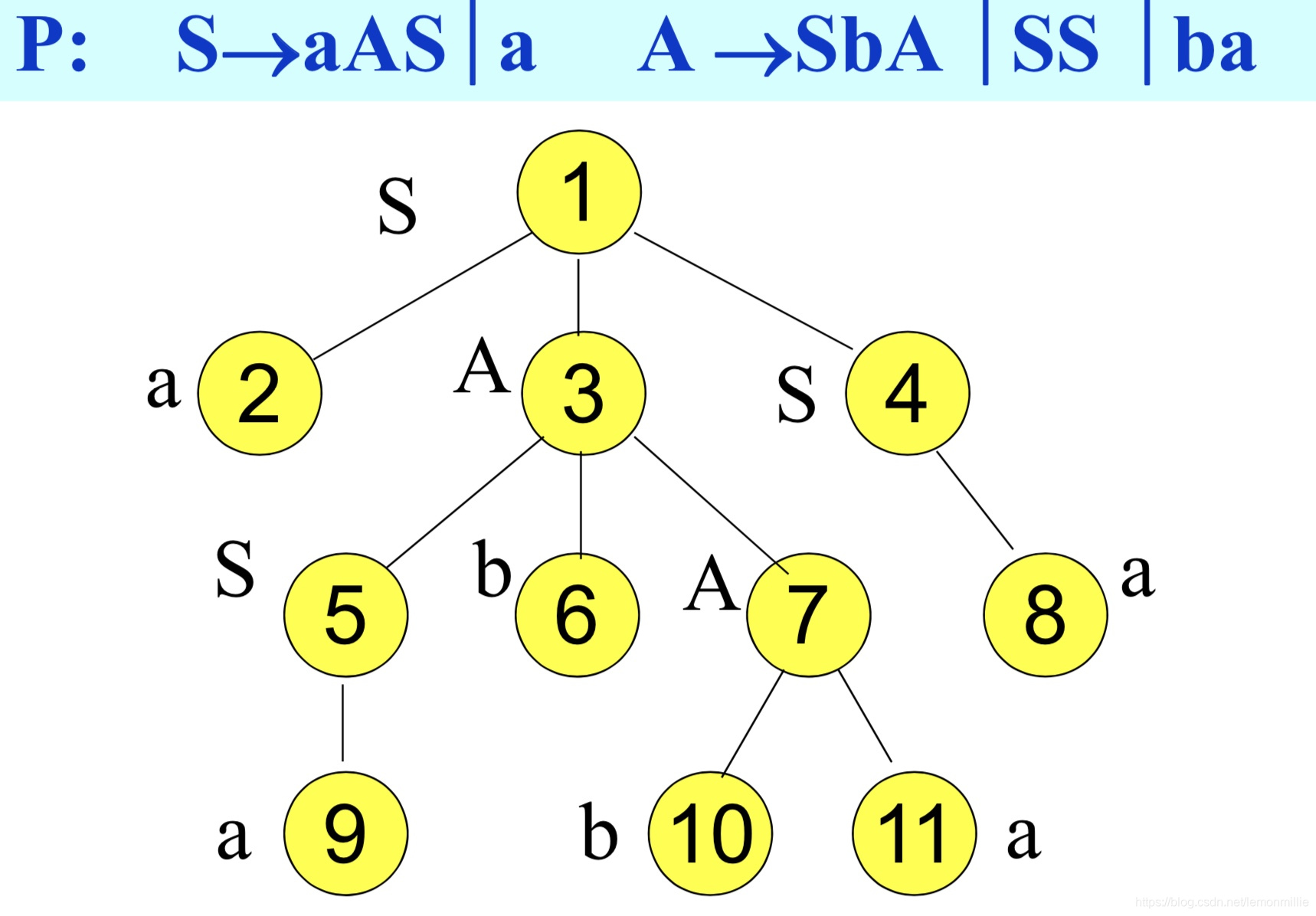
是字符串"aabbaa"的语法分析树，每个非叶子结点对应一个规则的使用

自顶向下构建语法分析树

就是从S开始往后推，先取一个token，判断可以用哪些规则，在这些规则里进行DFS和回溯，最后匹配完成。
当可以用的规则过多的时候，就要不断回溯，造成效率下降
8

FIRST的计算

ε\varepsilon指的是空串
9
10

FOLLOW的计算

11
一般coding题应该不会这么复杂，自己就能把这个东西手动分析出来

LL(x)文法： 只要看接下来的x个token是什么，就可以判断使用哪一条确定的规则。只有LL(1)方法用自顶向下效率才高

简单的表达式什么的可能都是LL(1)文法，LC 770，我们可以写出它的非左递归形式：

expr->term {'+'|'-'} expr | term
term->item '*' term | item
item->var | num | '(' expr ')'
  • 匹配item的时候，只要看下一个token是num、var或者'('就行了
  • 匹配完一个item之后，只要看下一个token是不是*就行
  • 匹配完一个term之后，只要看下一个token是不是+或-就行

###自底向上构建语法分析树
就是从字符串开始，不断寻找合适的规则，向前推到S
具体操作表现为移进-规约，就是维护一个符号栈，从左向右扫描token

  1. 如果操作为移进，token入栈
  2. 如果操作为规约，应用的是A→aBcA\rightarrow aBc，说明栈顶的符号依次为a、B、c，把它们pop出去，重新放一个A进去
  3. 最后栈中会只剩下一个起始符号

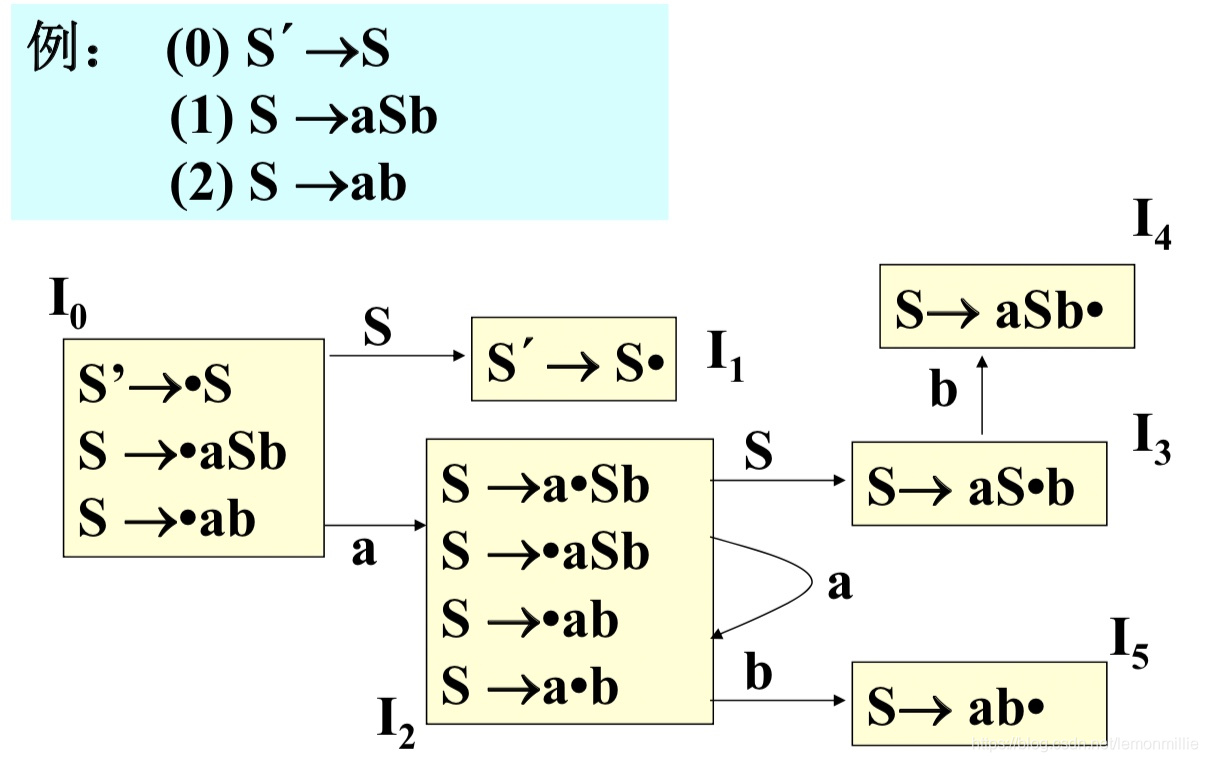
自底向上要配合LR分析表来使用：

  1. 首先要把P里的规则编号，然后总结出一个自动机，该自动机里每一个状态也要编号。
    12
  2. 然后构造分析表，规则如下：
    13
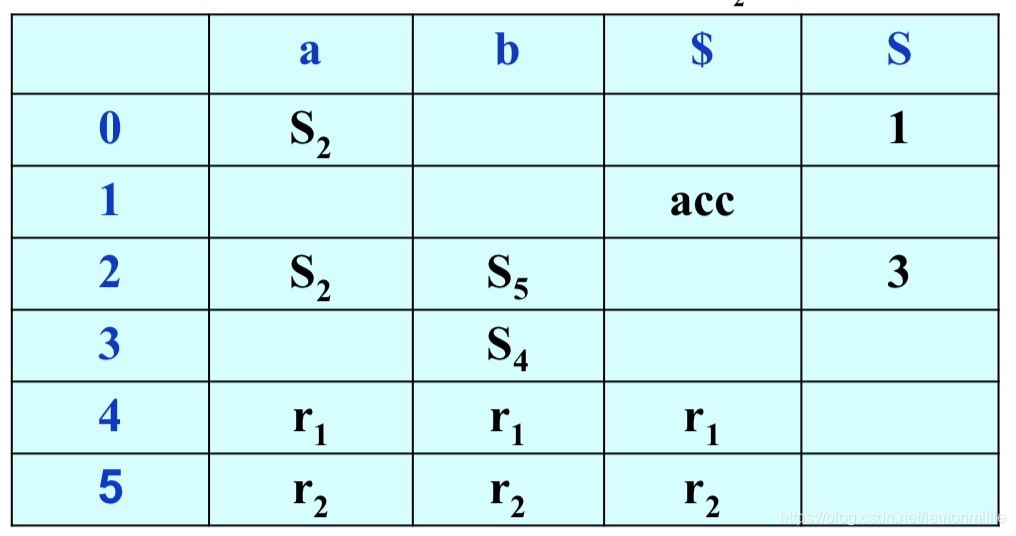
    得到：
    14
  3. 这个表怎么使用呢？我们维护一个栈，首先向栈中压入一个二元组('$',0)，表示现在处于状态I0。我们扫描token扫进来的肯定是非终结符号a，那么我们会遇到两种情况：
    1. 表里的动作是Si，说明要移进，移进这个符号就对应着自动机里的一次状态转移，转移到了状态Ii，那么我们把(a,i)压栈
    2. 如果表里的动作是rj，说明需要按照编号为j的规则进行规约，比如如果规则是A→aβbA\rightarrow a\beta b，那么这时候栈顶肯定是aa、β\beta、bb，把它们依次出栈，然后我们做完全规约之后其实相当于是扫描到了一个非终结符号A，这时候就要发生一次自动机里的状态转移，从现在栈顶的状态转到这个状态读入A之后的状态，具体如何转移要参照分析表。
      当然这只是适用范围很小的LR(0)分析。
      有时候会存在移进-规约冲突，这时候要用一些方法来判断用哪个规则
      以LC 770为例：
0: expr->expr {'+'|'-'} term
1: expr->term
2: term->term '*' item
3: term->item
4: item->var
5: item->num
6: item->'(' expr ')'

自动机不画了，比较复杂，直接上状态和表吧：
15
在I1、I3和I6都存在着移进-规约冲突，没关系，我们只要判断后面那个token是啥就能知道是移进还是规约了：
16

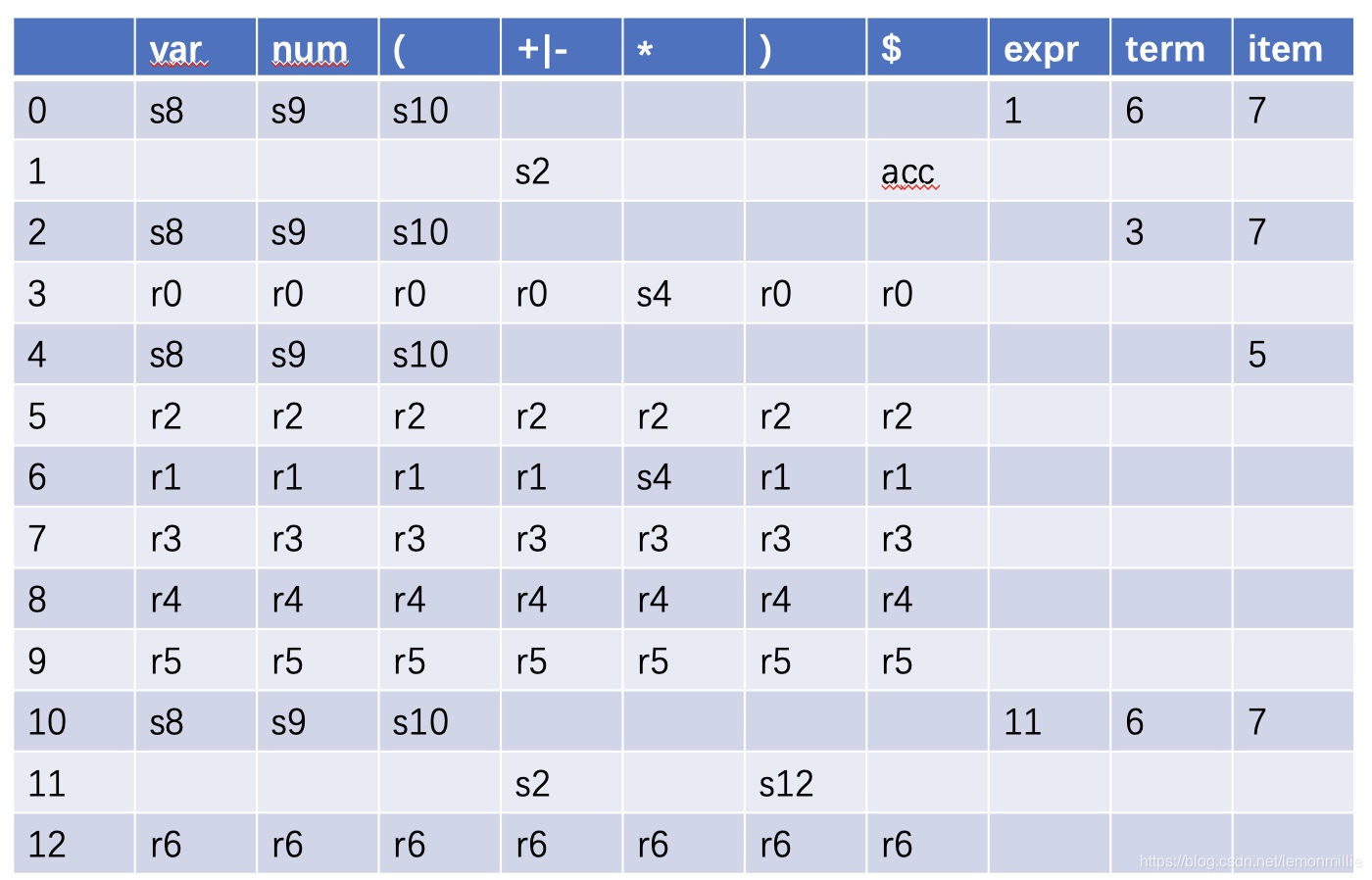
把这种方法用在解题上的实例详见LC 770的解答

posted @ 2019-02-06 22:05  milliele  阅读(1393)  评论(0)  编辑  收藏  举报