倾心讲解 FFT 多项式与快速傅里叶变换 && 迭代模板带注释
FFT 在 OI 中用于 O(nlogn) 快速计算大整数乘法、快速计算多项式的卷积等等.
这篇文章比较长, 是笔者耗费心血完成的, 为给徘徊于理解 FFT 的人一些绵薄之力, 如果读者能耐心地跟着笔者的思路走完全文, 相信读者一定会搞懂.
* 想要弄懂 FFT, 首先要明白多项式的点值表达是什么
如下为四个多项式的系数表达. 其中令 C(x) = A(x) + B(x), D(x) = A(x) * B(x).
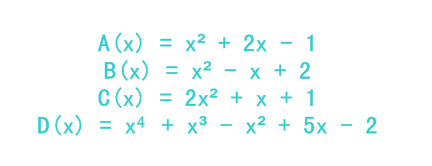
在计算 D(x) 时, 是用 A(x) 的每一项去乘 B(x) 的每一项. 这样的复杂度是 O(n^2), 效率极低.
所谓点值表达, 就是选几个 x 的值, 带入多项式求得相应的值 y, 写成 (x, y) 的形式.
每一个多项式都代表一个函数图像, 假设它的最高次项是 n 次的, 那么在图像上任选 n + 1 个点就可以确定这整个图像.
比如两个点确定一个一次函数, 三个点确定一个二次函数.
那我们就把上面四个多项式写成点值表达的形式:
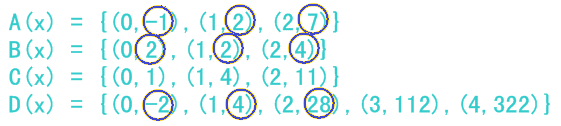
咦? 当 x 相同时, Dy = Ay * By? 有了这个规律, 我们就可以根据两个多项式的点值表达 O(n) 求出它们乘积式的点值表达 !
如果能快速完成点值表达与系数表达间的转换, 那就可以高效计算两个多项式的乘积了! ヾ(◍°∇°◍)ﾉﾞ
虽然任意 n + 1 个点就可以表示一个 n 次多项式, 我们在选取点的时候也不能瞎选, 要选择一些特殊的点来提升算法效率.
如何选取这些点呢?
* 我们先来了解一些必要的概念做一下铺垫
> 复数
实数的延伸, 它使任一多项式方程式都有根.
复数通常用 a + b * i 的形式表示, 其中 a, b 为实数, i 为 sqrt(-1). 也就是一个实数项加上一个虚数项.
实数 R 为复数 C 的一个子集, 相当于 b = 0 的情况.
> 复平面
复平面中, x 轴表示实数, y 轴(除了原点)表示虚数.
每一个复数 a + b * i 都可以表示为一个由原点 (0, 0) 指向点 (a, b) 的向量.
向量的模长就是它的长度, 即
.
向量的幅角是从 x 轴正半轴到该向量的转角的有向角（以逆时针为正方向）.
复数相加遵循平行四边形定则; 复数相乘时, 模长相乘, 幅角相加.
> 单位根
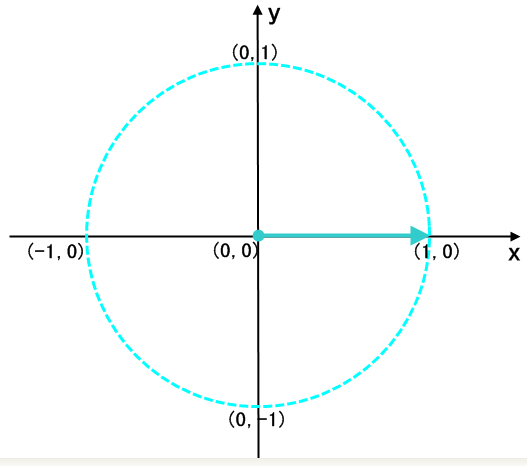
下图为 4 次单位根 :
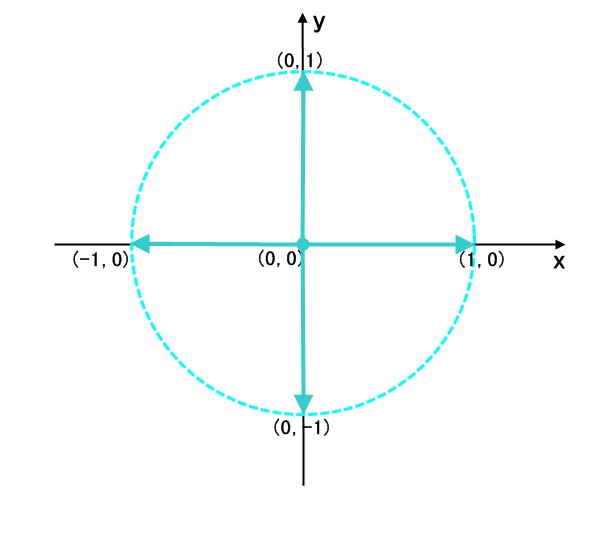
下图为 8 次单位根 :
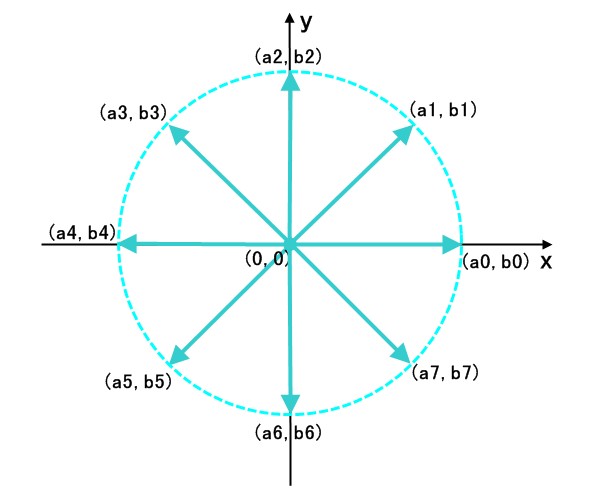
可以看出, n 次单位根当于单位向量绕原点逆时针旋转, 每次旋转 2π / n （相当于 360 / n 度）, 每次到达的点 (a, b) 所表示的复数 a + b * i 就是一个单位根.
我们将旋转的次数记为 m, 将一个 n 次单位根记做 
, ω 读作 "ou mi ga". 下文为方便叙述写成 ω(n,m) 的形式.
> 单位根的性质
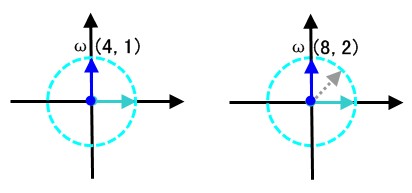
① ω(n,m) = ω(2n,2m)
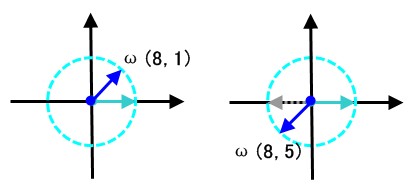
② ω(2n,m) = -ω(2n,n+m)
③ ω(2n,m)² = ω(n,m)
图示 ① :
图示 ② : ( ω(2n,n) 相当于转一半, 在此基础上再转 m 即 ω(2n,n+m) , 就相当于 -ω(2n,m) )
图示 ③ : ω(2n,m)² = ω(2n,2m), 这样就变成 ① 了, 就不放图了.
* 铺垫完毕, 回到问题 "点值表达要选择哪些点" ?
对于一个多项式 A(x), 我们要选取其在 { ω(n,0), ω(n,1), ω(n,2), ……, ω(n,n-1) } 处的点值. 其中 n 为 2 的幂次.
比如一个三次多项式, 我们要选取 4 个点确定它的点值表达, 这 4 个点的横坐标分别为 { ω(4,0), ω(4,1), ω(4,2), ω(4,3) }. 这里 4 恰为 2 的幂次.
普遍地, 对于一个 n 次多项式, 若 n + 1 不是 2 的幂次, 我们就选取一个大于 n + 1 的最小的 2 的幂次. 比如一个五次多项式, 6 个点就可以完成点值表达, 但 6 不是 2 的幂次, 所以我们应选取 8 个点.
为什么要选取单位根作为点值表达? 因为单位根具有特殊的性质, 下面我们就可以利用这些性质来提升算法效率.
为什么要选取 2 的幂次个点? 这里先留一个坑, 请接着看下去.
* 如何利用单位根的性质将多项式快速转换成点值?
首先, 我们把多项式 A(x) 按奇偶次幂分成两部分, 如下 :
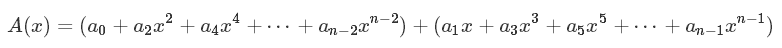
然后令
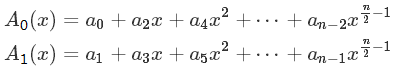
A0(x) 相当于把 A(x) 前半部分的 x² 换成 x; A1(x) 相当于把后半部分提取出公因式 x, 再把 x² 换成 x. 由此得出:
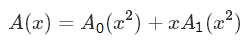
由于我们选择的 x 都是单位根, 所以写成 ω(n,m) 的形式 :
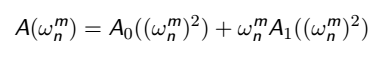
当 m < n/2 时, 由单位根性质 ③ ω(2n,m)² = ω(n,m) 可得 :
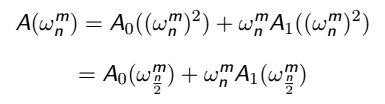
当 m >= n/2 时, 我们把 m 写成 m' + n/2.
然后由上文所述的性质可得 :
综合这两个式子, 可以发现, 若知道 A0(x) 和 A1(x) 在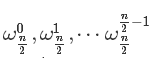
处的点值, 就可以 O(n) 求出 A(x) 在 
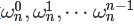处的点值. 而每次计算的范围都是折半的, 所以最多计算 logn 次, 所以复杂度就是 O(nlogn) 的了.
看到这里, 就可以明白为什么要选取 2 的幂次个点了. （因为每次的范围都折半呐~）
回顾一下上面的操作, 我们选取单位根作为 x, 然后将其代入多项式求得对应的 y, 就得到了一些点(x, y), 完成多项式的点值表达. 这个操作就是著名的 FFT.
是不是很容易?
到这里, 还没有结束, 因为上面讲的是怎么把多项式转换成点值, 接下来我们就要讲一讲怎么把点值转成多项式, 下面这个操作称为逆FFT.
* 如何将点值快速转换成多项式?
先来看一个多项式 :
我们将其写成矩阵乘法的形式 :
那一坨 ω 是一个范德蒙德矩阵, 第 i 行的公比是 ω(n, i - 1). 了解一下就好.
现在已知点值表达, 也就是已知 A 和 B 要去求 C, 那就用 A 除以 B, 相当于 A 乘以 1 / B , 而 1 / B 就是 B 的逆矩阵.
所以现在要求矩阵 B 的逆矩阵, 逆矩阵就是与 B 相乘等于 E (单位矩阵) 的矩阵.
非常巧的是, 我们只要对矩阵 B 中每一个元素取共轭复数并除以 n, 就得到了逆矩阵. 这个可以举个例子模拟一下.
共轭复数是实数部分相等, 虚数部分为相反数的复数, 相当于复平面上关于 x 轴对称的向量, 比如 ω(4,1) 的共轭复数为 ω(4,3).
然后我们再用 A 去乘以这个逆矩阵, 就可以得到多项式的系数矩阵 C 了.
这个相乘的过程跟 FFT 操作一样, 依然利用单位根的特殊性质, 分成奇偶两部分, 只不过原来是求 B * C, 现在是求 B 的逆矩阵 * A.
* 迭代实现
然而每次分成奇偶递归实现的效率很低, 这里有个巧妙的方法, 观察下面的范围 :
可以发现, 后序列是原序列的二进制翻转, 相当于一个反向的二进制加法.
为什么说是反向的二进制加法, 因为原序列是每次从右端加 1 地递增, 翻转后, 就是每次从左端加 1.
所以操作时, 模拟这个反向加法, 将序列翻转, 直接更新就可以了.
* 代码
#include <cstdio> #include <cmath> #include <algorithm> const double PI = acos(-1.0); const int N = 1e7 + 10; int n, m, L, R[N]; struct Complex { double x, y; Complex() {} Complex(double a, double b) : x(a), y(b) {} Complex operator + (const Complex & r) const { return Complex(x + r.x, y + r.y); } Complex operator - (const Complex & r) const { return Complex(x - r.x, y - r.y); } Complex operator * (const Complex & r) const { return Complex(x * r.x - y * r.y, x * r.y + y * r.x); } } a[N], b[N]; int read() { int x = 0; char c = getchar(); while (c < '0' || c > '9') c = getchar(); while (c >= '0' && c <= '9') { x = (x << 3) + (x << 1) + (c ^ 48); c = getchar(); } return x; } void FFT(Complex *A, int f) { for (int i = 0; i < n; ++i) if (i < R[i]) std::swap(A[i], A[R[i]]); //根据R[i]转成目标序列(最底层) for (int i = 1; i < n; i <<= 1) { //层数 Complex wn(cos(PI/i), f*sin(PI/i)); //n次单位根 for (int j = 0, r = i << 1; j < n; j += r) { //枚举要合并的每一块的起始点,周期为r Complex w(1, 0); //单位向量 for (int k = 0; k < i; ++k, w = w * wn) { //蝴蝶操作 Complex x = A[j+k], y = w * A[i+j+k]; A[j+k] = x + y, A[i+j+k] = x - y; //配对 } } } } int main() { n = read(), m = read(); for (int i = 0; i <= n; ++i) a[i].x = read(); for (int i = 0; i <= m; ++i) b[i].x = read(); m = n + m; for (n = 1; n <= m; n <<= 1) ++L; //L表示最小的大于等于n+m的2的幂次 for (int i = 0; i < n; ++i) R[i] = (R[i>>1]>>1)|((i&1)<<(L-1)); //R[i]表示i的二进制位翻转后的数字(二进制位数为L) FFT(a, 1), FFT(b, 1); for (int i = 0; i <= n; ++i) a[i] = a[i] * b[i]; FFT(a, -1); for (int i = 0; i <= m; ++i) printf("%d ", (int)(a[i].x / n + 0.5)); //四舍五入 return 0; }
