最长不下降子序列 NlogN && 输出序列

　　刚入学时学的算法，已经忘的差不多了，回顾一下。

　　对于普通的最长不下降子序列，每个数都要从头开始遍历，复杂度 $O(n^2)$，只能处理 $10^4$ 以内的数据。

　　刚刚学弟问我，就写了一下普通版的，顺便贴一下，这是 $openjudge$ 上的最长上升序列。

 

 

 

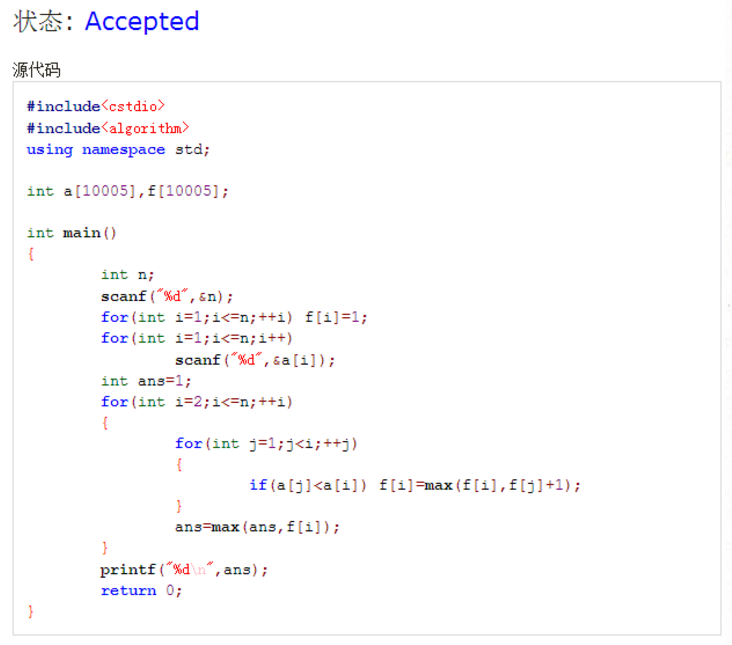
　　废话不多说，$nlogn$ 的算法如何实现？

　　利用序列的单调性。

　　对于任意一个单调序列，如 $1\ 2\ 3\ 4\ 5$（是单增的），若这时向序列尾部增添一个数 $x$，我们只会在意 $x$ 和 $5$ 的大小，若 $x>5$，增添成功，反之则失败。由于普通代码是从头开始比较，而 $x$ 和 $1,2,3,4$ 的大小比较是没有用处的，这种操作只会造成时间的浪费，所以效率极低。对于单调序列，只需要记录每个序列的最后一个数，每增添一个数 $x$，直接比较 $x$ 和末尾数的大小。只有最后一个数才是有用的，它表示该序列的最大限度值。

　　实现方法就是新开一个数组 $d$，用它来记录每个序列的末尾元素，以求最长不下降为例，$d[k]$ 表示长度为k的不下降子序列的最小末尾元素。

　　我们用 $len$ 表示当前凑出的最长序列长度，也就是当前 $d$ 中的最后那个位置。

　　这样就很 $easy$ 了，每读入一个数 $x$，如果 $x$ 大于等于 $d[len]$，直接让 $d[len+1]=x$，然后 $len++$，相当于把 $x$ 接到了最长的序列后面；

　　如果 $x$ 小于 $d[len]$，说明 $x$ 不能接到最长的序列后面，那就找 $d[1...len-1]$ 中末尾数小于等于 $x$ 的的序列，然后把 $x$ 接到它后面。举个例子，若当前 $x==7,len==8$：

1	2	3	4	5	6	7	8
2	3	4	7	7	10	12	29

　　$d[1]\cdots d[5]$ 均小于等于 $x$，若在 $d[1]$ 后接 $x$，则 $d[2]$ 应换成 $x$，但 $d[2]==3$，比 $x$ 小，能接更多的数，用 $7$ 去换 $3$ 显然是不划算的，所以 $x$ 不能接 $d[1]$ 后。同理，$d[2]\cdots d[4]$ 均不能接 $x$。由于 $d[5]\le x$ 且 $x<d[6]$，$7$ 能比 $10$ 接更多的数，所以选择在 $d[5]$ 后接 $x$，用 $x$ 替换 $10$。

　　根据这个操作过程，易知数组 $d$ 一定是单调的序列，所以查找的时候可以用二分！二分效率是 $logn$ 的，所以整个算法的效率就是 $nlogn$ 的啦~

　　对于最长不下降，可以用 $stl$ 中的 $upperbound()$ 函数，比如上述操作可以写为：

     for (int i=2;i<=n;i++)
     {
        if (a[i]>=d[len]) d[++len]=a[i];  //如果可以接在len后面就接上 
        else  //否则就找一个最该替换的替换掉 
        {
            int j=upper_bound(d+1,d+len+1,a[i])-d;//找到第一个大于它的d的下标 
            d[j]=a[i]; 
        }
     }

　　但是，对于其他的单调序列，比如最长不上升等等，需要根据情况来手写二分。

　　注意 $upperbound$ 是找单增序列中第一个大于 $x$ 的，$lowerbound$ 是找单增序列中第一个大于等于 $x$ 的，只要不是这两个，都需要手写二分。

　　代码：

//最长不下降子序列nlogn  Song 

#include<cstdio>
#include<algorithm>
using namespace std;

int a[40005];
int d[40005];

int main()
{
    int n;
    scanf("%d",&n);
    for (int i=1;i<=n;i++) scanf("%d",&a[i]);
    if (n==0)  //0个元素特判一下 
    {
        printf("0\n");
        return 0;
    }
    d[1]=a[1];  //初始化 
    int len=1;
    for (int i=2;i<=n;i++)
    {
        if (a[i]>=d[len]) d[++len]=a[i];  //如果可以接在len后面就接上 
        else  //否则就找一个最该替换的替换掉 
        {
            int j=upper_bound(d+1,d+len+1,a[i])-d;  //找到第一个大于它的d的下标 
            d[j]=a[i]; 
        }
    }
    printf("%d\n",len);    
    return 0;
}

 

　　关于最长序列的序列输出，网上有讲解说 $nlogn$ 算法的缺点是不能输出序列，当时刚上高中的我很不服气，于是花了一天自己搞出来了 $nlogn$ 的序列输出代码。

　　当时写的：

　　“想了好久，认为 $nlogn$ 做法也是可以输出序列的，这时候需要增加一个 $c$ 数组 用来记录每个元素在最长序列中的位置，即 c[i] 表示 a[i] 被放到了序列的第几个位置。

　　输出时，从 数组 a 的尾部开始，逆序依次找出 c 为 len, len-1, len-2 … 3, 2, 1 的元素，并且找到一个就接着寻找 c[i]-1，直到找到 c[i] 为 1 的数。

　　举个例子：

a:	13	7	9	16	38	24	37	18	44	19	21	22	63	15
c:	1	1	2	3	4	4	5	4	6	5	6	7	8	3

　　len = 8;

　　我们从 15 开始倒着找 c 为 8 的元素，找到 63，接着找 c 为 7 的，找到 22，再找 c 为 6 的，找到 21，再找 c 为 5 …… 以此类推。

　　从而，我们得出的序列为 63，22，21，19，18，16，9，7

　　逆序输出来，就是 7，9，16，18，19，21，22，63

　　为什么这个方法是对的呢？倒序查找保证了两个条件：

　　　　- 如果 c 中有多个相同的数，后面的一定是最新更新的；

　　　　- 在保证一条件的前提下，倒序找，后面的数一定可以接到前面数的后面。”

 　代码：

//From - Milky Way

#include <cstdio>
#include <algorithm>
#include <stack>
using namespace std;

int d[100], c[100], a[100], len = 1;

int main() {
    int n; scanf("%d", &n);
    for (int i = 1; i <= n; ++ i) {
        scanf("%d", &a[i]);
    }

    d[1] = a[1], c[1] = 1;
    for (int i = 2; i <= n; ++ i) {
        if (d[len] <= a[i]) {
            d[++ len] = a[i], c[i] = len;
        } else {
            int j = upper_bound(d + 1, d + len + 1, a[i]) - d;
            d[j] = a[i], c[i] = j;
        }
    }

    stack<int> sta;
    for (int i = n, j = len; i >= 1; -- i) {
        if (c[i] == j) {
            sta.push(a[i]); --j;
        }
        if (j == 0) break;
    }

    printf("%d\n", len);
    while (!sta.empty()) {
        printf("%d ", sta.top());
        sta.pop();
    }

    return 0;
}