增强学习笔记 第十二章 资格迹

资格迹Eligibility Traces是RL中一项基本技术，Sarsa, Q-Learning等一切TD类方法，都可以用资格迹来提升学习效率。提升效率的方式是不用等到n-step再去更新n步前的value。

资格迹和n-步Bootstrap一样，将MC和TD进行了统一。

 

12.1 λ回报

在第七章中我们有

我们可以采用不同n值的任意线性组合来对参数进行更新，只要它们权和为1。

 

我们定义

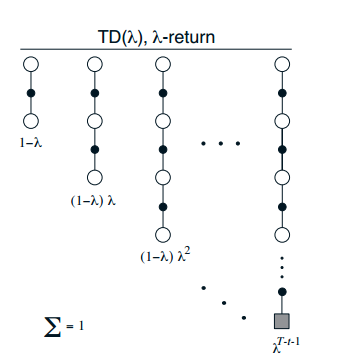
对应参数的更新迭代式

 

不同λ的值和不同的n-step值产生的效果类似：

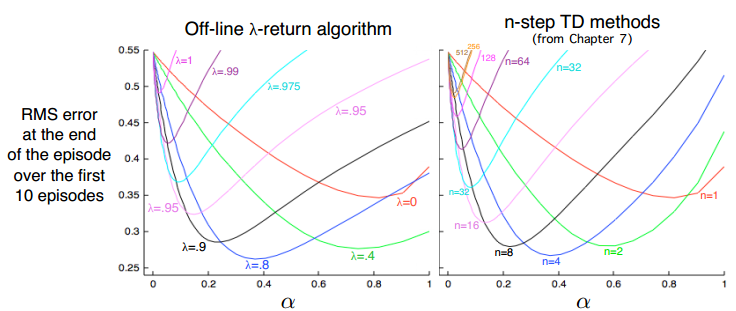
这是一个离线算法，因为需要一个episode执行完才能更新θ。

执行完之后，回头在每一步观察后面各步的回报，并通过更新\theta校正对应的v/q值：

 

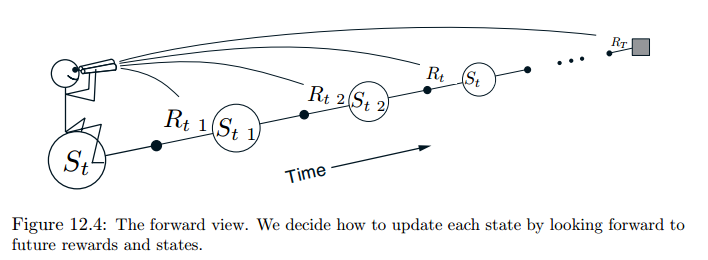
 12.2 TD(λ)算法

根据上面的off-line算法，我们做一些改进，我们在每一步都更新参数θ，而不是等到最后一步。早更新效率通常会更好，另外也把计算量均匀地分摊了。

这里我们引入资格迹向量，称为accmulative trace：

TD误差为：

迭代更新式为：

理解上面的式子，我们把$\boldsymbol e_t$展开为

$\boldsymbol e_t=\nabla\hat v(S_t,\boldsymbol \theta_t)+\gamma\lambda\nabla\hat v(S_{t-1},\boldsymbol \theta_{t-1})+\gamma^2\lambda^2\nabla\hat v(S_{t-2},\boldsymbol \theta_{t-2})+\cdots+\gamma^{t-1}\lambda^{t-1}\nabla\hat v(S_1,\boldsymbol \theta_1)$

然后代入至$\boldsymbol\theta$的迭代式中，有：

$\theta_{t+1}=\theta_t+\alpha(\delta_t\nabla\hat v(S_t,\boldsymbol \theta_t)+\gamma\lambda\delta_t\nabla\hat v(S_{t-1},\boldsymbol \theta_{t-1})+\gamma^2\lambda^2\delta_t\nabla\hat v(S_{t-2},\boldsymbol \theta_{t-2})+\cdots+\gamma^{t-1}\lambda^{t-1}\delta_t\nabla\hat v(S_1,\boldsymbol \theta_1))$

观察式子，实际上更新了每一步的v值。并且和12.1中的式子近似，只是更新θ的时机顺序不同导致最后结果会有细微差别。

 

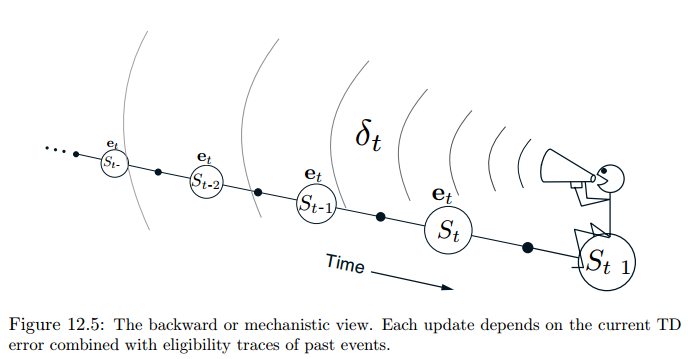
12.3 在线观点

我们定义h截断λ回报

可以理解为在h就终止的λ回报。

对每个episode，我们定义\theta_0^h$均为上一episode更新完之后的\theta值，然后计算每个截断点的$\theta_t^h$

 

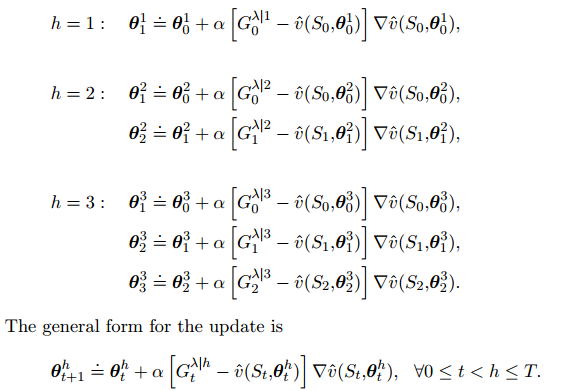
 12.4 真在线TD(λ)

将上一节的θ序列排成三角形：

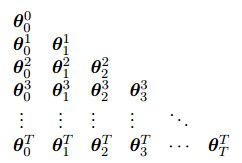
我们需要的只是对角线上的值。在episode中，每走一步，就计算出一排。但这样计算太繁琐了。对于线性近似，我们可以用下面的式子来简化计算：

其中

可以证明由此可以正确产生对角线上的θ值。

 

上面的$\boldsymbol e_t$我们成为dutch trace，是为了和12.2中的$\boldsymbol e_t$作区分(accumulating trace)。之前对tile coding中的binnary features还出现过replacement trace，但是现在已经被dutch trace替代

 

12.5 蒙特卡洛学习中的dutch trace（略）