增强学习笔记 第九章 On-Policy预测的近似

对于状态空间太大的问题，表格类方法无法存储这么大的价值表，也没有办法穷尽这么多的状态。考虑到很多状态是相似的，知道一个状态的价值也就大概知道类似状态的价值，因此可以采用函数近似的方法，函数近似是监督学习的一个应用。

这一章我们主要做价值函数的近似。我们定义一个N维参数$\boldsymbol \theta$, N比状态数量小很多，$\theta$可以是线性规划的权重，也可以是神经网络的权重，还可以是决策树的分叉点。得到$v_{\pi}(s)\approx \hat v(s,\boldsymbol \theta)$

 

9.1 价值函数近似

我们将每一次backup操作当成一个监督学习中的样例。但并不是所有监督学习方法都适用于增强学习，增强学习需要支持在线学习，并且需要支持非平稳的目标函数。

 

9.2 预测目标

对表格类方法来说，不同状态的价值函数是可以独立学习的，但是对近似方法来说，可能产生连带效应。改善一个状态的价值预测有可能损害其他状态的价值预测。因此需要知道哪个状态我们最重视。定义

其中$d(s)$表示该策略下状态经历的时间比重。定义$h(s)$为$s$作为初状态比例（已知），$\eta(s)$为episode中经历的次数（未知）。解下列方程组

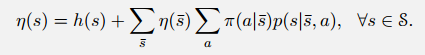
可以得出$\eta(s)$，从而算出$d(s)$

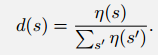
采用MSVE的理由并不是十分明确，毕竟我们的最终目标是改善policy，而不是最小化平方误差，但是实践中我们没有找到明确更好的指标。

我们的目标是找到一个最优的$\theta^*$使得MSVE最小。

 

9.3 随机梯度下降和半梯度方法

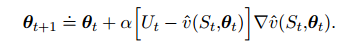
这个式子并不是严格的梯度下降，如果采用bootstrap的话，$U_t$本身也和$\theta$相关。这时候只能称为半梯度算法，实践中该方法有较好的收敛性，至少在线性方法中，是保证收敛的。

  

 

9.4 线性方法

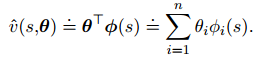
取梯度有：

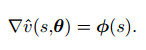
 得出迭代式：

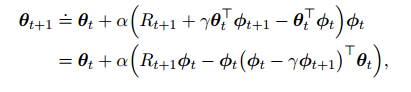
对两边取期望：

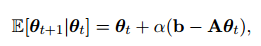
其中

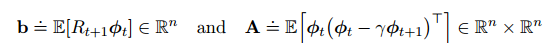
当收敛时，有$\theta_{t+1}=\theta_t$，可以得出：

 

9.5 线性方法的特征构造

因为线性方法具有高效、收敛等优良特性，我们需要它设计一系列特征构造方法。

特征的选择需要应用先验知识，保证和任务相关。同时我们也需要组合特征，因为线性方法并不能处理特征之间的组合性。例如在倒立车问题中，杆子很低是很危险的，但是这时候如果有很大的向上的角速度，则我们认为是安全的。

 

9.5.1 多项式基

对d状态变量来说，每个状态是一个d维实数向量，因此基函数可以表示为：

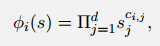
其中$c_{i,j}$是0到N之间的整数

i为基函数索引,j是状态分量索引。

因此共有$(N+1)^d$个基函数。

 

9.5.2 傅里叶基

傅里叶基可以以任意精度来逼近任何函数，对[0,T/2]区间的逼近来说，可以只保留cos部分。

我们假定T=2，实现[0,1]区间函数的逼近，N阶基函数为：

$\phi_i(s)=\cos(i\pi s)$

对d维(0,1)立方体来说，状态s表示为$(s_1,s_2,\cdots,s_d)^T$，基函数为：

$\phi_i(s)=\cos(\pi\boldsymbol c^i\cdot \boldsymbol s)$

共有$(N+1)^d$个基函数，其中$c_j_i$表示第i个基函数第j个状态分量的系数

傅里叶基的拟合能力比多项式基通常要好

 

9.5.3 Coarse Coding

在状态空间中画一系列的圈，如果状态在圈中，则对应的feature为1。这样就构造出了一系列二值feature。

圈圈的大小在初期会影响函数拟合，大圈圈通常会泛化的更宽。

如果圈圈数量足够多，并不会影响拟合的精细度。在后期就可以体现出来。

 

9.5.4 Tile Coding

对状态空间的网格划分称为tiling，网格中的小正方形称为tile。

 

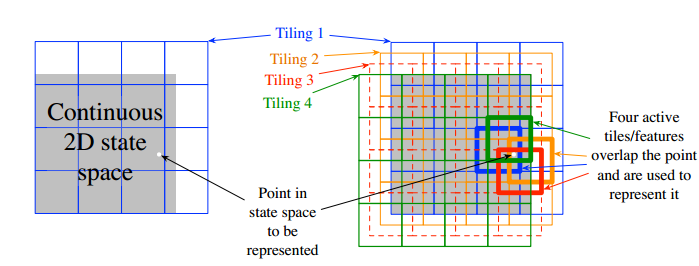
对d维状态来说，第一个tiling通常采用(1,3,5,...,2d-1)作为tiling之间的间隔。而tiling的个数则为大于等于4d的2的幂方。

 

9.5.5 径向基

径向基是对Coarse Coding在连续值上的推广。它的feature值可以是[0,1]上的实数。

 

径向基有平滑性和可导性，但是实际上并没有显示太好的性能，它的计算负担也比tile coding更重。在高维度空间中，tile的边界变得比较重要，而径向基函数的表现不尽如人意。

 

9.6 神经网络

在RL中，神经网络可以使用TD误差来学习价值函数。通常1-2层的隐藏层具有较好的效果。

 

9.7 LSTD （略）