增强学习笔记 第七章 多步Bootstrap
多步TD是介于单步TD和MC之间的一种方法
7.1 多步TD预测
首先,定义n-step return:
![]()
![]()
![]()
得出n步迭代更新:
![]()
其中$G_t^{(n)}$满足下列误差递减性质:
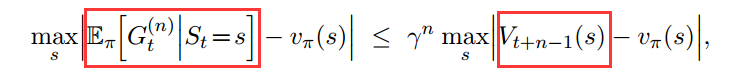

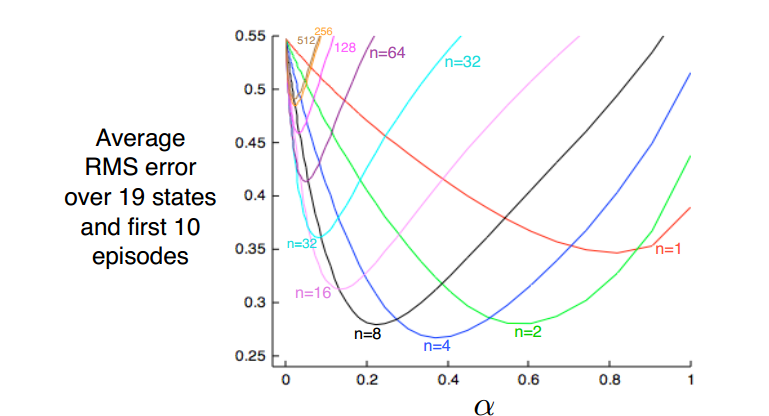
当n取一个折衷值的时候,平方误差最小
7.2 n步Sarsa
将状态价值换为动作价值,重新描述$G_t^{(n)}$:
![]()
以及迭代更新式:
![]()
对应的,Expected Sarsa的G值:
![]()

7.3 n步off-policy学习
Recall that off-policy learning is learning the value function for one policy, π, while following another policy, µ. Often, π is the greedy policy for the current actionvalue-function estimate, and µ is a more exploratory policy, perhaps ε-greedy.
![]()
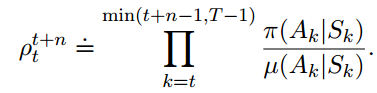
例如,如果$\pi$中某个动作的概率是0,那么这个更新应该被忽略,如果$\pi$中某个动作的可能性更高,那么自然也应该赋予更高的更新系数。
现在照旧用Q来代替V,得到Sarsa更新式:
![]()

off-policy通常比on-policy要收敛得慢。
7.4 去掉Importance Sampling的Tree Backup算法
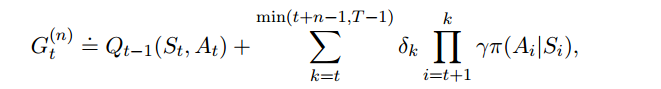

7.5 Importance Sampling和Tree Backup的组合(略)



