增强学习笔记 第二章 多臂赌博机问题

2.1 k臂赌博机问题

定义action value为期望奖励：

通常用平均值来估算：

2.2 action value方法

贪心法是一直估算值最大的action

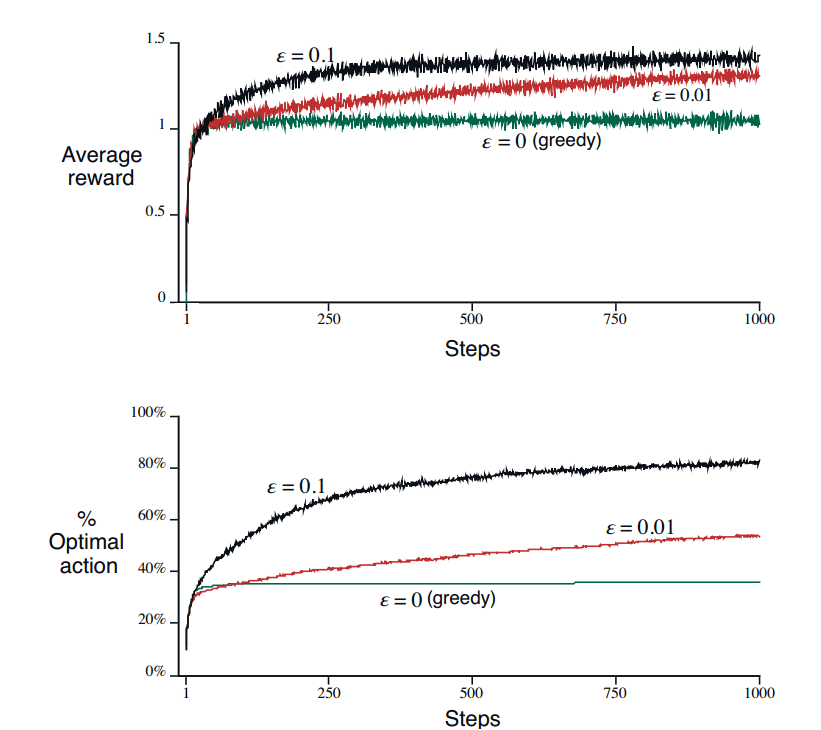
$\epsilon$贪心是指以$\epsilon$的概率随机选择一个action。对于方差较大的问题来说，选择较大的$\epsilon$效果较好。

2.3 增量实现

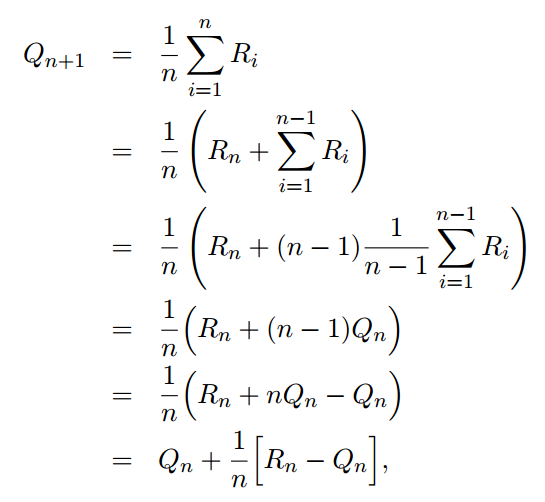
2.4 非平稳问题

对非平稳问题使用一个不变的常数来迭代。

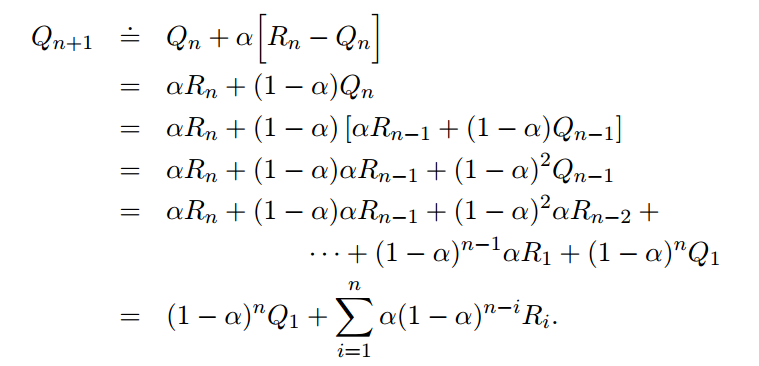
使用常数作为step-size，最终值不会收敛。收敛的条件是：

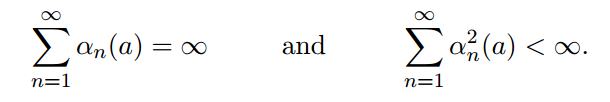
2.5 乐观初始值

采用乐观初始值，能鼓励exploration，使得所有的action被使用更多次。在后期会表现更好

 

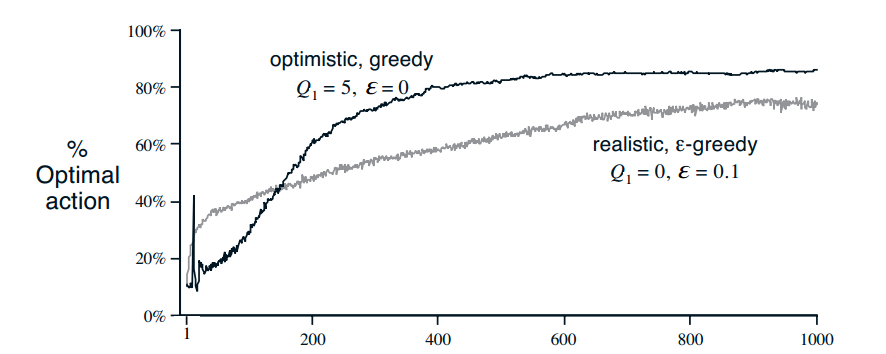
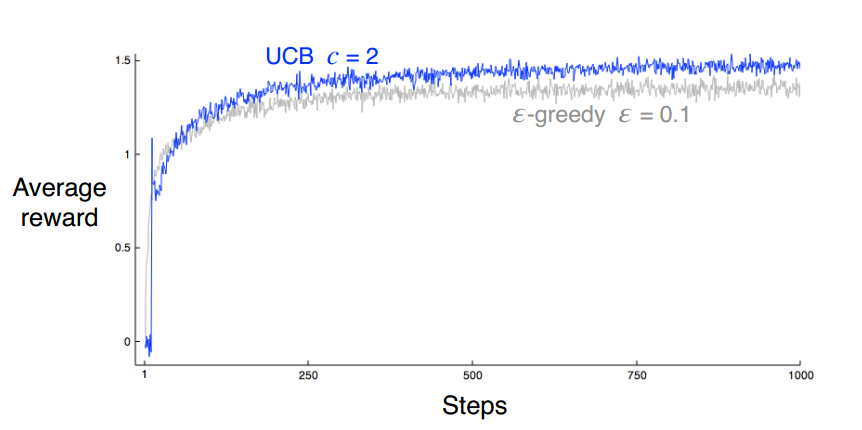
2.6 UCB 动作选择

可以看到，时间越长，增益越少，选择次数越少，增益越多

 2.7 梯度赌博机算法

之前都是使用action value来确定使用哪个action。现在我们绕过action value，直接定义一个偏好$H(a)$，然后通过softmax函数来确定$\pi$

 

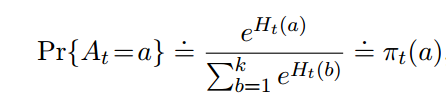
迭代过程如下：

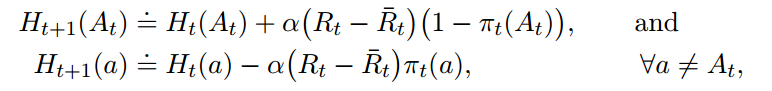
这个梯度算法类似于机器学习中的梯度下降。梯度下降是通过调节参数来使得loss最小，这里是通过调节h来使得$E[R_t]$最大

对比梯度下降的算法，那么更新算法就是

而

通过推导最后可得出上述迭代过程