1.概念陈述
成法，即为已经存在的方法，他是经过时间的洗礼、先哲们千锤百炼而流传下来的具有解决已知问题成效的方法.
改法，即为在已经存在的方法之上加以修改，使之成为具备解决普遍问题的方法，此即为改法.
新法，即具备解决未知问题的方法.
开法，即具备解决未知的一类问题的一般方法.
2.例子
lim(x->0)（x^2*e^(1/x^2)）
=lim(x->0) e^(1/x^2)/(1/x^2)
=lim(t->∞) e^t/t
=lim(t->∞) e^t
＝∞
洛必达法则，结果为∞，此处，洛必达法则即为成法.
接下来，谈改法
例如，完全有理三角和为如下形式的和：
S(ψ,q)=∑eq(ψ(x))，x∈(1,q)，x∈N+.
其中，ψ(x)是整系数的多项式，许多作者得到了关于S(ψ,q)的估计的结果，在此基础之上，我们可以改进该方法，形式如下：
S(R,q)=∑eq(R(x))，x∈(1,q)，x∈N+.
其中，R(x)是有理函数，于是，得到了关于S(R,q)的上界的一些新结果.
接下来，谈新法
分数阶积分估计不等式
假设
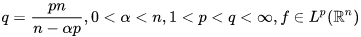
那么
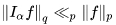
其中
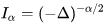
此即为新法.
接下来，谈开法
举例来说，设y为方程y+y+6=0的根，则扩域中的整数环为，即所有a+by形式的数，其中，a和b为一般的整数，环中一个非主理想的例子是，但这个理想的立方为主理想，实际上，这个环的理想类群是一个3阶的循环群，与此对应的类域是添加方程w−w−1=0的根w，从而获得的扩域：非主理想2a+yb的一个理想数是ι =(−8−16y−18w+12w+10yw+yw)/23，由于，满足ι−2ι+13ι−15ι+16ι+28ι+8=0，它是一个代数整数，类域的整数环中的所有乘以ι会得到中元素的元素都具有aα+bβ的形式，其中：
α=(−7+9y−33w−24w+3yw−2yw)/23，β=(−27−8y−9w+6w−18yw−11yw)/23.
α和β也是代数整数，满足：
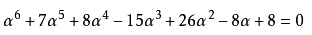和
同时，将aα+bβ乘以理想数ι后就会得到非主理想2a+by.
此即为开法.
3.小结
在关于方法理论问题的研究中，如果，在前人的基础之上，能够改进前人的方法（哪怕一点点），那么，你就步入科研之路了.
