积分，简而言之，可以分为不定积分与定积分，不定积分只是导数的逆运算，而定积分是求一个函数的图形在一个闭区间上和x坐标轴围成的面积，定积分的正式名称是黎曼积分，用黎曼自己的话来说，就是把直角坐标系上的函数的图象用平行于y轴的直线把其分割成无数个矩形，然后把某个区间[a,b]上的矩形累加起来，所得到的就是这个函数的图象在区间[a,b]的面积，实际上，定积分的上下限就是区间的两个端点a,b，在一定条件之下，函数f(x)在闭区间[a,b]上的定积分(黎曼积分)为：
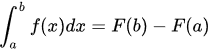
我将不定积分与定积分(黎曼积分)都叫作一般积分，黎曼积分的核心思想就是试图通过无限逼近来确定这个积分值，我们称这个积分值为黎曼和，但是，黎曼积分也有一些不可积的问题，例如：狄利克雷函数，狄拉克δ函数.
狄利克雷函数
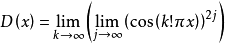
狄拉克δ函数
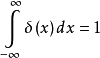
这时，我们就要推广黎曼积分，以求能解决一些不可积的问题.
我们知道，黎曼积分他是面积的推广，在相当广泛的场合，他也够用了，但是，随着人们对客观世界的不断深化，特别是在18世纪，有关热，波，电磁等的研究需要，数学上必须对函数项级数，含参变量的函数等进行更深入的探讨，若导数是质点运动的速度，加速度的表达，那积分就是表达功，能量的重要思想，随着物理学的发展，迫切需要一个比黎曼积分更有效的积分，他既保持黎曼积分的直观性，又能在逐项积分方面比黎曼积分所需的条件有较大的改进，于是，勒贝格积分产生了.
在闭区间a和b之间对函数f的积分可以被看作是求f的函数图像下的面积，对于多项式这样比较常见的函数来说这个定义简而易懂，但是对于更加稀奇古怪的函数来说它是什么意思呢?广义地来说，对于什么样的函数“函数图像下的面积”这个概念有意义?这个问题的答案具有很大的理论性和实际性意义，19世纪里在数学中有把整个数学理论放到一个更加坚固的基础上的趋势，在这个过程中数学家也试图给积分计算提供一个稳固的定义，黎曼提出的黎曼积分成功地为积分运算提供了一个这样的基础，黎曼积分的出发点是构造一系列容易计算的面积，这些面积最后收敛于给定的函数的积分，这个定义很成功，为许多其它问题提供了有用的答案，但是在求函数序列的极限的时候黎曼积分的效果不良，这使得这些极限过程难以分析，而这个分析比如在研究傅里叶级数、傅里叶变换和其它问题时却是极其重要的，勒贝格积分能够更好地描述在什么情况下积分有极限，勒贝格积分所构造出的容易计算的面积与黎曼积分所构造的不同，这是勒贝格积分更加成功的主要原因，勒贝格的定义也使得数学家能够计算更多种类的函数的积分，比如输入值为无理数时函数值为0，输入值为有理数时函数值为1的狄利克雷函数没有黎曼积分，但是有勒贝格积分.
