C语言常用数据类型说明

 1、取值范围：

   short一般占两个字节，取值范围：-32768 - 32767
   int一般占两个或四个字节，取值范围：-2147483648 - 2147483647

   unsigned int一般占四个字节，取值范围：0 - 4294967295

   long long一般占8个字节，取值范围：-9223372036854775808 - 9223372036854775807
   float一般占4个字节，取值范围：1.17549 e-038 - 3.40282 e+038
   double一般占8个字节，取值范围：2.22507 e-308 - 1.79769e+308

   对unsigned类型进行取负操作是无意义的，因为得到的数还是unsigned，比如这个代码中的n永远不会是负数：int n = -sizeof(DataType)。

   不要将unsigned类型与signed类型进行运算或者比较操作，因为默认的类型转换会发生不可预期的结果，如下所示：

　　unsigned int n = 0;
　　long long i = -1 + n; //-1默认转换为了unsigned int类型，导致i的结果为4294967295
　　bool b = n > -1; //-1默认转换为了unsigned int类型，导致b为fasle

   可以使用std::numeric_limits<int>::max()、std::numeric_limits<double>::lowest()、std::numeric_limits<double>::min()来获得各类型的最大、最小值（min获得的是最小正值，lowest获得的是最小负值或者0）。

   isnan()：判断一个浮点型（或整形）变量是否是一个非正常的数值。

   isinf()：判断一个浮点型变量是否是一个无穷大值(正无穷大或负无穷大)。

   isalnum(int): 判断所传的字符是否是字母（a-z，A-Z）和数字（0-9）。

   isdigit() / isaplha(): 判断所传的字符是否是数字 / 字母。

   isspace()：判断判断传入的字符是否是空格。

   isblank() : 判断传入的字符是否是空白字符（'\t'、' '）。

   isupper() / islower()：判断传入的字符是否是大写 / 小写字母。

   toupper() / tolower()：获得对应字符的大写 / 小写版本。

　　%d: int
　　%l : long
　　%lld : long long
　　%f，%lf : printf中%f对应float和double，在scanf中%f对应float，%lf对应double。
　　%u : unsigned int
　　%lu : unsigned long
　　%llu : unsigned long long
　　%e/%E: 浮点数的科学计数法
　　%g 自动选择%f或%e
　　%x 无符号十六进制整数

    %5.2：指定字符串宽度的最小值为5，字符串宽度达不到的话使用空格补充；对于%f指定小数位数为2，对于%d指定指定输出数字的最小位数为2（达不到2位的话补0），对于%s指定输出字符的最大个数。

    %-：字符串左对齐，默认为右对齐。

    %+：显示正负号。

    %05：指定字符串宽度最小为5，字符串宽度达不到的话使用0补充。

    对于格式化输出，%f、%lf 默认输出的小数位数是6位：

    double dd = 123.45678912;
    printf("%lf", dd); //输出为123.456789

    double d = 1234.56;
    char buf[100] = { 0 };
    sprintf_s(buf, "%f", d); //buf为1234.560000

    d = 123.123456789;
    memset(buf, 0, 100);
    sprintf_s(buf, "%lf", d); //buf为123.123457

    对于浮点型推荐使用double来代替float。以下是浮点型数值的一些截取方法：

    //地板
    double n1 = std::floor(-13.9); //-14
    double n2 = std::floor(13.9); // 13

    //天花板
    double n3 = std::ceil(-13.1); //-13
    double n4 = std::ceil(13.1); // 14，天花板

    //取最近的数，即四舍五入
    double num5 = std::round(-14.5); //-15
    double num6 = std::round(14.5); // 15

    //与round不同的是如果左右最近的两个数距离相等（小数部分是0.5）的话取最接近的偶数
    double num7 = std::rint(-14.5); //-14
    double num8 = std::rint(14.5); // 14

 

    后缀意义：F表示float，U表示unsigned int，L表示long, LL表示long long。

    前缀意义：0b为二进制表示，0为八进制表示，0x为十六进制表示。

2、由于各数据类型所占字节数与编译器和CPU有关，所以我们永远不要想当然的认为int大小为4（16位下int大小为2）、指针大小为4（64位程序下指针大小为8）、short大小为2等来使用，稳妥的方法是使用sizeof()。
3、一般情况下我们使用int来存储整型，因为它既可以满足4字节对齐，也可以满足我们存储日常使用的数字，但当数值可能超过十亿这种等级的时候我们应该选用long long。

4、关于移位运算

　右移>>的话，对于左边空出来的位补上与符号位相同的值。

　对于short、char等低于int的类型会先自动转换为int后再移位。

　对于int类型的移位，移动的位数超出31位的话实际移动位数是对32进行的求余结果，如 3 >> 32 相当于 3 >> 0，3 >> 33相当于 3 >> 1。　

5、运算符的结合性与优先级

　　结合性为从右向左运算的有三种：赋值=、单目运算符、三目运算符，各运算符的优先级为：

　　

6、内存中存储方式

字符型：
char占一个字节，最高位用来表示正负，取值范围为-2^7到2^7-1（-128-127），故可表示2* 22^7个数值，即-128到127。对应ascii取值范围为。
unsigned char占一个字节，由于其没有符号位，取值范围为0到2^8-1（0-255），故可表示2^8个数值，即0到255。

字符串中一个反斜杠表示转义，比如'\n'表示换行符，'\t'表示制表符，如果想要表示反斜杠字符的话使用'\\'，如下所示：

    char c = '\n'; //换行符
    char* p = "abc\tdef";  // abc     def

  在字符串常量中，如果想要表示反斜杠字符的话使用'\\'，比如下面的字符串常量以及对应的表示内容：

 

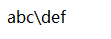
在字符串常量中，如果想要在引号中使用引号的话，使用\"，比如面的字符串常量以及对应的表示内容：

 

 

   

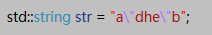
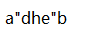
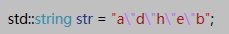
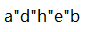
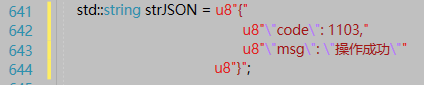
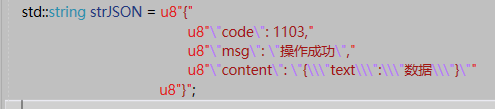
如果使用字符串常量来表示一个JSON对象，这个JSON中的一个元素值又是一个JSON对象的话，那么这个里面JSON对象属性的引号需要使用\\\"来表示，前面两个\\表示一个反斜杠，后面的\"表示一个引号，比如下面的字符串常量以及对应的表示内容：

  

除了L、_T()包围，我们还可以使用R"()"包围，使用它的话不会对字符串里进行任何转义，同时使用多行文本的话更方便，如下所示：

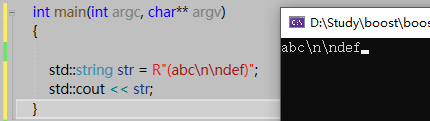
使用R"()"包围的话可以很方便的表示JSON字符串，u8R"()"表示使用UTF-8字符编码：

整型：

int在32位系统下占4个字节，最高位用来表示正负，故可表示2* 2^31个数值，取值范围为-2^31-2^31-1。

最小取值问题：
有一个问题就是char跟int的最小取值为什么是-2^7和-2^31而不是2^7-1和-2^31-1？以下答案部分转载和参考CSDN网友daiyutage的文章。
拿char类型来说，一共8位，1位为符号位，所以剩下7位来表示数值，根据排列组合得出char可表示的数值总数为2^7 * 2，它们就是+0到127和-0到-127，那么已经看出问题来了：出现了两个0，一正一负，原码分别为0000 0000、1000 0000，我们知道，0其实既不是正数也不是负数，所以0只用原码0000 0000来表示，而0的补码为全部位数取反后再加一即1 0000 0000，忽略溢出的1比特(0是唯一计算补码过程中会出现溢出的数字)，得出0的补码跟原码相同。那么就多出了一个-1的原码1000 0000，其补码也是全部位数取反后加一，得到跟原码相同的补码1000 0000。使用这个多出来的-1的原码可以用来表示-128，那么为什么它用来表示-128而不是其它值呢？理论上-128的原码应为1 1000 0000，最高位为符号位，取反加一后的补码也为1 1000 0000，可以看出-128的原码跟补码丢弃最高位后与-0的相同，而且即使截断后的-128和char 型范围的其他数(-127~127)运算也不会影响结果， 所以才可以用-0来表示-128。简而言之就是：因为有一个符号位，所以就会出现+0和-0，而用-0就用来表示-2^7即-128了。

负数：
在计算机中，数值是用补码来存储的，正数的补码是其原码，负数的补码是原码除符号位外各位取反后加1。

例1：
char a = 1; //a的补码：0000 0001
char b = -1; //b的补码：1111 1111
char c = a ^ b; //c的补码即为1111 1110, 而原码为1000 0010即-2
printf("%d\n", c);//所以输出为-2

例2：

int A = 468; //a的二进制：0000 0001 1101 0100
char B = A; //int赋给char，舍去高位，只剩低位：1101 0100，符号位是1，所以是负数的补码，再减1取反后得1010 1100即-44
printf("%d", B); //所以输出为-44

浮点型：

  十进制转二进制：整数采用“除2取余，逆序排列”的方法，如13除2商6余1，6除2商3余0，3除2商1余1，1除2商0余1，遇到商为0结束，按照逆序排列余数，所以13的二进制表示为1101。小数采用“乘2取整”法，如0.8125乘2为1.625，取整1，小数部分0.625继续乘2为1.25，取整1，小数部分0.25乘2为0.5，取整0，0.5乘2为1，取整1，遇到小数部分为0结束，所以0.8125的二进制表示为0.1101。所以13.8125用二进制表示的话就是1101.1101。

  二进制转十进制，比如1101.1101，整数部分：1×2的3次方为8 + 1×2的2次方法为4 + 0×2的1次方为0 + 1×2的0次方为1 = 13，小数部分：1×2的-1次方为0.5 + 1×2的-2次方法为0.25 + 0×2的-3次方为0 + 1×2的-4次方为0.0625 = 0.8125，所以1101.1101转换成十进制就是13.8125。

  浮点型在内存中是以二进制的科学计数法形式存储的，一个float使用32位存储，一个double使用64位存储，如下所示，对于float的话，符号位占1位（0为正，1为负），指数位占8位，剩余的23位为尾数位，存储整数和小数值。比如86.5（float）的二进制表示为1010110.1，使用二进制的科学计数法则为1.0101101e6，因为是整数所以符号位为0，指数为6所以指数位应该为00000110，但是指数实际上使用偏移量方式存储（具体原因见下段描述），比如指数为6的话实际存储6+127=133即10000101，读取的时候再减去偏移量127，整数和小数为1.0101101，所以尾数位为1010 1101 0000 0000 000，但是因为采用二进制科学计数法表示数值的话，整数位肯定为1（比如1.0101101e6），所以23位只用来存储小数部分即可，所以尾数位实际存储0101 1010 0000 0000 000。读取该float的时候，符号位为0所以为正数，指数位为10000101即133，所以实际指数为133-127即6，实际的尾数要在尾数位前加1即1 0101 1010 0000 0000 000，这样就可以推导出该数为1.0101101e6即1010110.1。

  浮点型二进制科学计数法中的指数其实并不是直接作为一个char来存储的，而是将其转换成一个无符号类型来存储，转换的方法是将指数加上偏移量127，比如指数为-120的话实际存储7（-120+127=7），指数为100的话实际存储227（100+127=227），即实际存储的数=指数+127，所以指数=实际存储的无符号数-127，又因为8位的话能存储的无符号数范围为0到255，所以单精度的指数取值范围为0减127到255减127，即-127到128，所以单精度能表示的最大值为1.111...(小数点后23个1)乘2的127次方，。使用偏移量来将指数转换为正数来存储的话，效率会比直接存储为char效率更高，比如当比较两个浮点数大小的时候，直接将“符号位+指数位+尾数位”这32位整体当做一个32位的无符号数，从高位到低位逐位比较即可（1000比0111要大）：符号位不同的话，正数肯定大于负数，符号位不同，比较指数位，指数大小可以直接决定二者大小，符号位和指数位都相同，再比较尾数位。

float:

double:

  对于浮点数来说，如果8位指数位全为1，即存储的值为255的话，用来表示一些特殊值（非规格化数）。比如8位指数位全为1，尾数位全为0，符号位为0表示正无穷大，符号位为1表示负无穷大。8位指数位全为1，尾数位不全为0的话就表示非数值NaN，如下所示（单精度）。因为指数位全为1表示特殊值，所以单精度浮点数的指数最大为1111 1110(即254)-127=127，所以单精度浮点数能表示的最大数为：符号位0 指数位1111 1110 尾数位11111111111111111111111，使用科学计数法表示为1.11111111111111111111111e127，十进制的话约等于3.4乘10的38次方（C++中FLT_MAX宏）。0.0也属于浮点型中的非规格化数：如果指数位全是0（实际指数0-127=-127），尾数位也全为0，那么这个数就表示0.0。因为指数位全0的话表示特殊值，所以指数位最小是0000 0001，实际指数是0000 0001（即1）-127=-126。综上所述，float的指数最小为-126，最大为127，指数为-127或128的话表示特殊值。

  

  十进制转二进制的时候，对于整数部分采用“除2取余”的方法，所以肯定会有商为0结束的时候，但是对于小数部分的话，因为是采取“乘2取整”的方法，所以很有可能会遇到乘2后小数部分一直不为0的情况，所以有效数字就超过了float的23位（或者即使算到了小数为0的话有效数字也超过了23位），对于这种情况，会采用舍或者入的方式来保存有效数字。如下所示，0.8转二进制的话位数无限循环，所以只能截取（舍或者入）保存，所以我们将0.8赋给一个float变量的话，调试的时候查看该变量的值会发现其是一个比0.8要大一点点的数，比如是0.800000012，而如果给float变量赋值0.7的话，查看该变量值会是0.699999988，这就是对23位之后保存不了的尾数进行舍或者入的结果。

  

  浮点数里的小数转二进制的时候，尾数部分很有可能是一个无限循环的数，或者即使不是无限循环的话，尾数部分也超过了23位，从而导致精度问题（舍或者入的截断）。那如果浮点数里边没有小数，只有整数的话，会不会出现精度问题呢？答案是会的。整数表示成二进制的话，位数太长就会出现精度问题，比如16777217.0转换成二进制为1+23个0+1，用科学计数法表示的话，尾数部分长度为24，超出最长的23位，所以会出现截断，实际保存的值为16777216.0。整数的长度越长尾数不一定越长，比如1099511627776.0，其转换为二进制的话为1+40个0，用科学计数法表示的话为1e40，尾数位长度为0，完全没有精度问题。绝对值小于等于16777215（（16777215转换为二进制为24个1，科学计数法表示的话尾数为23个1））的整数float，一定不会有精度问题，因为绝对值小于等于16777215的尾数长度小于等于23。绝对值大于16777215的整数float，可能会出现精度问题（比如前面说的16777217），也可能不会出现，比如16777216这种比16777215大但是却是2 的整数次幂的数，就没有精度问题，因为16777216转二进制是1+24个0，科学计数法表示为1*2的24次方，尾数长度为0（尾数位为8个0）。

  float的尾数为23位，加上前面固定的1的话总位数为24位，如果要保存的浮点数的尾数超过23位（比如该浮点数的尾数是无限循环），需要进行入，所以实际存储的尾数的第23位就是进行舍入后的值，也就是说尾数的前22位是准确的，再加上前面固定为1，所以可以说前23位是准确的。而如果是要进行舍操作的话，是将23位之后的数值进行舍去，所以尾数的23位都是准确的，再加上前面固定的1的话，可以说24位都是准确的，这就是说float二进制有23或24位有效数字（精度）的缘由。而二进制转换成十进制的话，log10(2的23次方)≈6.92，，有效数字（精度）为6或7位。比如将1234567891.0赋给float变量的话，因为二进制的尾数太长所以将23位之后的值进行了舍操作，调试查看该变量实际值的话是1234567940.0，可以看到误差出现在十进制的第7位之后。将0.8赋给一个float变量的话，因为二进制的尾数太长所以第23位进行了入操作，所以该变量实际值为0.800000012，误差出现在十进制的7位之后。而如果给float变量赋值0.7的话，因为二进制的尾数太长所以将23位之后进行了舍操作，查看该变量值会是0.699999988，误差出现在十进制的7位之后。而且这里所说的位数其实是科学计数法表示下的（因为二进制是科学计数法表示的），比如double类型的0.000123456789，转换成十进制的科学计数法为1.23456789e-4，将其赋值给float变量的话，该变量实际保存的值为1.23456790e-4，可以看到误差出现在7位之后。所以说单精度float有 6-7 位十进制有效数字，双精度double有 15-16 位十进制有效数字也是如此得出的。而且精度位数是从非0的数值开始算起的，比如将0.0006赋值给float，实际存储值为0.000600000028，可以看到小数点后10位都是精精确的，而0.6赋值为float的话，其值为0.600000024，可以看到小数点后7位是精确的。

  因为浮点数存在误差，所以我们判断两个浮点变量是否相等的话，除非这两个变量是同类型的直接赋值，可以使用==来判断是否相等（如下所示），其它的情况下的话都应该使用一个阈值（或者叫容差）来比较二者是否相等，如果二者差值的绝对值小于这个容差的话，就认为二者是相等的。

    float f1 = 0.2F; //实际保存的值：0.200000003
    float f2 = 0.2F; //实际保存的值：0.200000003
    if (f1 == f2) {
        int a = 0; //会进入
    }

    float f3 = 0.2F; //实际保存的值：0.200000003
    double f4 = 0.2; //实际保存的值：0.20000000000000001
    if (f3 == f4) {
        int a = 0; //不会进入
    }

    float f5 = 0.3F; //实际保存的值：0.300000012
    float f6 = f5 * 3.0F; //实际保存的值：0.900000036
    float f7 = 0.9F; //实际保存的值：0.899999976
    if (f6 == f7) {
        int a = 0; //不会进入
    }

  

  当一个浮点型的整数位太长，或者小数位转换为二进制后一直不能取整，或者二者兼有之，都会导致二进制的尾数太长，超过23位的部分被舍或者入。比如1.28存储到float的话实际存储为1.27999997，误差为0.000000003，12.8存储到float的话实际存储为12.8000002，误差为0.0000002，可以看到误差值随数值变大而变大（因为12.8转二进制为1100.110011001100110011001100...，前面的整数12已经占了4位，所以后面的小数最多只能保存20位，在20位小数处会进行舍入；而如果是1.28的话，会在23位的小数处进行舍入，误差更小）。再比如将123456789.0赋给float变量的话，float中实际保存的值为123456792.0，误差为3；而将0.7存储到float的话实际值是0.699999988，误差仅为0.000000012。

由于浮点型的值可能存在误差，所以我们判断两个浮点型是否相等的话直接使用==是不准确的，如果两个double之差的绝对值小于DBL_EPSILON的话就可以认为是相等的：

    float f = 0.7F; // 0.699999988
    double d = f;
    double _d = 0.7; // 0.69999999999999996

    if (d == _d)
    {
        int a = 0; //不会进入
    }
    if (abs(d - _d) < FLT_EPSILON)
    {
        int a = 0; //会进入
    }
    if (abs(d - _d) < DBL_EPSILON)
    {
        int a = 0; //不会进入
    }

    double d1 = 0.1; //0.10000000000000001
    double d2 = 0.1;
    double d3 = 0.1;
    double dSum = d1 + d2 + d3; //0.30000000000000004
    double ddd = 0.3; //0.29999999999999999
    if (dSum == ddd)
    {
        int a = 0; //不会进入
    }
    if (abs(ddd - 0.3) < DBL_EPSILON)
    {
        int a = 0; //会进入
    }

  虽然我们可以使用FLT_EPSILON或DBL_EPSILON来判断两个浮点数是否相等，但是浮点数的误差还会引起多个浮点数相加的结果与预期不符问题。比如下面的float类型的f，有效位数为7-8位，所以其实际值为0.000234559993，这里就有了误差，而下面的123将其相加后理论上sum实际值应该为123.00023455993，但因为小数点前面的整数123又占用了三个有效位数，所以小数位数只剩下了四位有效数字，所以sum的实际值为123.000237，与我们期许的sum的准确值123.00023456存在0.00000244的误差：

    float f = 0.00023456; 
    float sum = 123.0F + f;

 而如果相加的浮点数不包含整数，全部是小数的话也会因为浮点数特殊的存储方式或者精度问题而产生误差：

    double d = 0.3; // 0.29999999999999999
    double sum = 0.0;
    for (int i = 0; i < 10; i++)
    {
        sum += d; // 2.9999999999999996
    }

    if (abs(sum - 3.0) < DBL_EPSILON)
    {
        int a = 0;
    }
    else
    {
        int a = 0; //会进入这里
    }

 对于上面的问题，可以将浮点型转换为整型使用来解决这个问题，如下所示，比如我们业务上仅会使用两位小数的话，那么可以将该浮点数乘100后使用整形保存。Java的话可以使用BigDecimal类型解决这个问题：

    double d = 0.03; //0.029999999999999999
    long long l = d * 100; //3
    
    long long sum = 0.0;
    for (int i = 0; i < 10; i++)
    {
        sum += l;
    }
    
    double _d = sum / 100.0; //0.29999999999999999
    if (abs(_d - 0.3) < DBL_EPSILON)
    {
        int a = 0; //进入这里
    }
    else
    {
        int a = 0;
    }

  上面的方法适用于业务上对于小数位数使用确定的情况，比如对于股价来说其最小单位为分，而对于小数位数无限制的业务情况，会出现问题，如下所示：

int main()
{
    double d = 0.009;
    long long l = d * 100;

    long long sum = 0.0;
    for (int i = 0; i < 10; i++)
    {
        sum += l;
    }

    double _d = sum / 100.0;
    if (abs(_d - 0.0) < DBL_EPSILON)
    {
        int a = 0; //进入这里
    }
    else
    {
        int a = 0;
    }
}