C. Diamond Miner

这题不应该做不出来的……主要是第二题用的是我不怎么用到的set并且花了很久。所以慌了（嗯，一定是这样）

由于距离计算只与坐标绝对值有关。故将负的值都转换为正值。

然后分别对于x和y排序即可。顺序摆放的代价一定不劣于逆序摆放

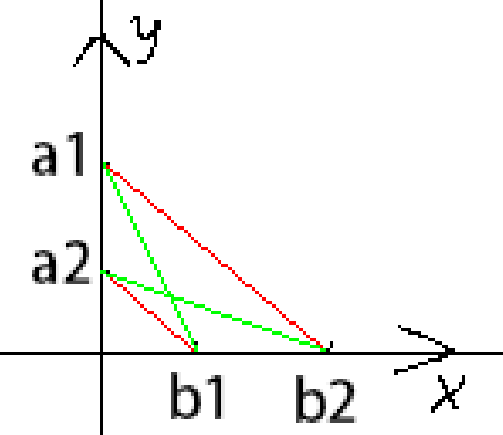
设x₁<x₂,y₁<y₂.则x₁~y₁+x₂~y₂<x₁~y₂+y₁~x₂

用这张图加上三角形两边之和大于第三边即可得出。故只要挨个选出最小的x和y进行计算即可（即不两边相交）。

（与之相似但结论相反的为排序不等式）

AC代码如下（记得开long long）：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<set>
#include<map>
#define MAXN 200005
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
int t,n;
ll x[MAXN],y[MAXN];
double ans;
int main(){
    scanf("%d",&t);
    while(t--){
        int xcnt=0,ycnt=0;
        ans=0;
        scanf("%d",&n);
        for(int i=0;i<2*n;i++){
            ll temp1,temp2;
            scanf("%lld%lld",&temp1,&temp2);
            if(temp1==0)
                y[ycnt++]=abs(temp2);
            else
                x[xcnt++]=abs(temp1);
        }
        sort(y,y+n);
        sort(x,x+n);
        for(int i=0;i<n;i++){
            ans+=sqrt(y[i]*y[i]+x[i]*x[i]);
        }
        printf("%.15llf\n",ans);
    }
    return 0;
}

D. Let's Go Hiking

本题是博弈思维题。（情况也有点多）

首先我们理解题意。

a只能向左或者向右移动一格并且只能移动到值比该点大的点。

b只能向左或者向右移动一格并且只能移动到值比该点小的点。

a先动，如果a，b中有人无法行动了，则输掉比赛。

判断a能赢的情况数

那么a就只能取在最长的单调序列的最大值处。（否则b就可以在最长的单调序列的最大值处）

如果是只有一个单调序列，即1,2,3,4,5，则若a选5，b则选4，a就会被堵死。

故a只能选择一个极大值点。即1,2,3,4,5,4,3,2,1中的5.这样a就不会被开局堵死。

需要注意左边的单调增序列长度须以右边的单调减序列长度一致。

还需要注意的是这两个单调序列必须是全数列中唯二最长的。

但是b如果发现无法堵上a且没有更长的路。就会从a所在的边进行殊死搏斗。

如果单调序列长度为奇数。则不管a走跟b同一序列还是相反序列则都是a赢。如为偶数则相反。

故最后还需要判断一下序列长度。

以及要处理一下最后一点的边界情况即可。

（综合一下a获胜只有一种情况。故答案只有1和0（a先手被坑了啊））

AC代码如下（略显复杂了。可以试一下分别向前和向后求一下最长连续上升子序列来求解）：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<set>
#include<map>
#define MAXN 100005
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
int n,p[MAXN],ans;
void judge(){
    int upcnt=1,downcnt=1,maxcnt=0;//记录上升序列个数和下降序列个数和最大单调序列个数
    int flag;//flag记录当前是上升序列（1）还是下降序列（0） 
    int ansflag=0;;//记录当前最大值是否可行 
    p[0]<p[1]?flag=1:flag=0; 
    for(int i=0;i<n-1;i++)
        if(p[i]<p[i+1]){
            if(flag==0){
                flag=1;
                if(upcnt==downcnt&&downcnt==maxcnt&&ansflag){ 
                    ansflag=0; 
                    ans=1;
                }else if(downcnt>maxcnt){
                    ansflag=1;
                    maxcnt=downcnt;
                    ans=0;
                }else if(downcnt==maxcnt){
                    ansflag=0;
                    ans=0;
                }
                upcnt=1;
            }
            upcnt++;
        }else{
            if(flag==1){
                flag=0;
                if(upcnt>maxcnt){
                    ansflag=1;
                    maxcnt=upcnt;
                    ans=0;
                }else if(upcnt==maxcnt){
                    ansflag=0;
                    ans=0;
                }
                downcnt=1;
            }
            downcnt++;
        }
    if(upcnt>maxcnt||downcnt>maxcnt){
        ans=0;
        return;
    }
    if(upcnt==maxcnt&&flag==1)
        ans=0;
    else if(upcnt==downcnt&&downcnt==maxcnt&&ansflag&&flag==0)
        ans=1;
    if(maxcnt&1)
        return;
    else
        ans=0;
    return;
}
int main(){
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%d",&p[i]);
    judge();
    printf("%d\n",ans);
    return 0;
}

E.Garden of the Sun

　　首先需要知道每个X之间都没有点和边。也就是说X周围的八格都是点

也就是说对一个x有

...

.x.

...

故我们可以每三行选出第一行填满x。再选择一列填一个x令第一行与下一组三行的第一行相连。

由于对于中间的其他x。其上面或下面都是.，故不会同时和两个满行相连。

因此两个满行中间只有一列相连。若两行中一个x都没有。则任意挑选一列铺上x

需要特别注意的是当行数为3的倍数时。最后一行所连接的满行并不存在。故需要特判一下。若最后一行存在x，则令其与上面的满行相连即可。

对于判断中间两行是否有x存在。我们只要判断其中一行即可。若有一行不存在x。则选择第一列，判断令一行的第二列是否有x，有则铺第二列，无则铺满第一列，这并不影响结果，且不会产生环。

（其实遍历检查两行也问题不大，因为数据较小）

本代码中选择了检查第三行。

AC代码如下：

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>
#define MAXN 505
using namespace std;
typedef pair<int,int> pii;
typedef long long ll;
int t,n,m;
char sun[MAXN][MAXN];
int main(){
    scanf("%d",&t);
    while(t--){
        memset(sun,0,sizeof(sun));
        scanf("%d%d",&n,&m);
        for(int i=0;i<n;i++)
            scanf("%s",sun[i]);
        for(int i=0;i<n;i++){
            if(i%3==0)//第一行涂满格 
                for(int j=0;j<m;j++)
                    sun[i][j]='X';
            else if(i%3==2){//判断第三行是否有x 
                int flag=0;
                for(int j=0;j<m;j++)
                    if(sun[i][j]=='X'){
                        sun[i-1][j]='X';
                        flag=1;
                        break;
                    }
                if(!flag)//第三行没有X 
                    if(sun[i-1][1]=='X')
                        sun[i][1]='X';
                    else
                        sun[i][0]=sun[i-1][0]='X';
            }        
        }
        if(n%3==0){//行数是3的倍数 
            for(int j=0;j<m;j++)
                if(sun[n-1][j]=='X'){
                    sun[n-2][j]='X';
                }
        }
        for(int i=0;i<n;i++)
                printf("%s\n",sun[i]);
    }
}

F.BFS Trees

直接洛谷题解吧orz。

我把他的代码注释了一下：

#include<bits/stdc++.h> 
#define i60 long long 
#define dou double 
using namespace std; 
const int N=405,skc=998244353;  
vector<int>v[N]; 
int n,m,d[2][N],c[N],s[2],ans[N][N],b[N] ;     
void add(int x,int y){ 
    v[x].push_back(y); 
}  
queue<int>q; 
bool cmp(int x,int y){ 
    return d[0][x]<d[0][y];
}
void bfs(int w){
    int x=s[w];//看这是哪个点
      memset(d[w],-1,sizeof(d[w]));
      q.push(x);
     d[w][x]=0;//第w个点到x距离为0（因为就是本身阿喂 
     while(!q.empty()){
        x=q.front();
        q.pop();
        int l=v[x].size(),y;
        for(int i=0;i<l;i++){
            y=v[x][i];
            if(d[w][y]!=-1)
                continue;
            d[w][y]=d[w][x]+1;
            q.push(y);
        }
      }
}
signed main(){ 
    ios::sync_with_stdio(false) ; 
    cin.tie(0);
    cin>>n>>m;
    int x,y;
    for(int i=1;i<=n;i++)
        b[i]=i;
    for(int i=1;i<=m;i++) 
        cin>>x>>y,add(x,y),add(y,x); //添边 
      for(int i=1;i<=n;i++) 
        for(int j=i;j<=n;j++){ //因为i,j和j,i是一样的，故只枚举j>=i的情况。后续处理即可 
            s[0]=i;//树的节点加入i和j 
            s[1]=j;
            bfs(0);//bfs记录i到每个点的最短距离 d[0][] 
            bfs(1);//bfs记录j到每个点的最短距离 d[1][]
            int cnt=0,dis=d[0][j];//记录i和j两点间的距离 
            for(int k=1;k<=n;k++)
                cnt+=(d[0][k]+d[1][k]==dis);//如果k在i，j之间，则cnt++ 
            if(cnt!=dis+1){ //i,j之间点的数量不等于i,j距离+1说明不止一条路在i,j之间。答案为0 
                ans[i][j]=0;
                continue;
            }//如果i,j之间 
            sort(b+1,b+1+n,cmp);//根据每个点到i的距离进行排序。 
            int nw=1;//nw为答案
            for(int k=1;k<=n;k++){
                x=b[k];//x=b[k]为距i第k大的点 
                if(d[0][x]+d[1][x]!=dis)//如果x不在i,j之间。那么就有c[x]种树可以构成。一开始进去的是0，故这一步会略过。先算c【】 
                    nw=1ll*nw*c[x]%skc;//乘法原理。总数相乘 
                  for(int p=0;p<(int)v[x].size();p++){//遍历与x相邻的点 
                       y=v[x][p];//y为与x相邻的点 
                    　　if(d[0][y]==d[0][x]+1&&d[1][y]==d[1][x]+1)//如果y不在i,j之间，代表多了一种树构成的可能性。
                        　　c[y]++;//初值为0；++后为1，此时并不会改变答案。但如果多次进入。即有多条路能连，则会改变 
                  }
            }
            ans[i][j]=nw;//记录答案
            for(int k=1;k<=n;k++)//清空可能性 
                c[k]=0;
          }
      for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++) 
            cout<<ans[min(i,j)][max(i,j)]<<' ';//令j,i的输出结果和i,j一致
        cout<<'\n';
      }
      return 0;
}

posted @ 2021-03-11 13:34 mikku 阅读(66) 评论(0) 收藏举报

刷新页面返回顶部

mikku

Codeforces Round #706 (Div. 2) (C~F)

公告