局部加权线性回归

     通常，选择交给学习算法处理特征的方式对算法的工作过程有很大影响。

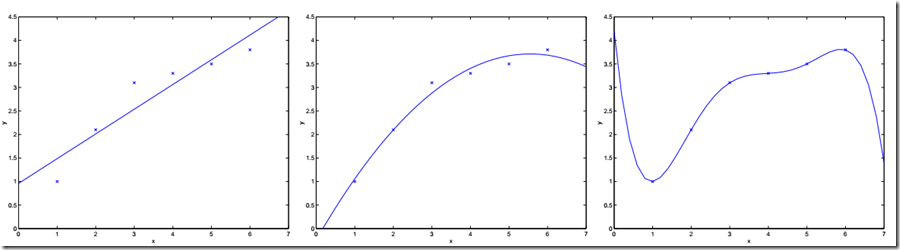
     例如：在前面的例子中，用\(x1\)表示房间大小。通过线性回归，在横轴为房间大小，纵轴为价格的图中，画出拟合曲线。回归的曲线方程为：\(\theta_0+\theta_1x_1\),如下边最左边的图。

     若定义特征集合为：\(x1\)表示房子大小，\(x2\)表示房子大小的平方，使用相同的算法，拟合得到一个二次函数，在图中为一个抛物线，即：\(\theta_0+\theta_1x_1+\theta_2x_1^2\)，如上边中间的图。

     以此类推，若训练集有7个数据，则可拟合出最高6次的多项式，可以找到一条完美的曲线，该曲线经过每个数据点。但是这样的模型又过于复杂，拟合结果仅仅反映了所给的特定数据的特质，不具有通过房屋大小来估计房价的普遍性，从而线性回归的结果可能无法捕获所有训练集的信息。

       所以，对于一个监督学习模型来说，过小的特征集合使得模型过于简单，过大的特征集合使得模型过于复杂。

对于特征集过小的情况，称之为欠拟合（underfitting）

对于特征集过大的情况，称之为过拟合（overfitting）

      解决此类学习问题的方法：

1) 特征选择算法：一类自动化算法，在这类回归问题中选择用到的特征

2) 非参数学习算法：缓解对于选取特征的需求，引出局部加权回归

参数学习算法（parametric learning algorithm）

定义：参数学习算法是一类有固定数目参数，以用来进行数据拟合的算法,线性回归即是参数学习算法的一个例子。通常该固定的参数集合设为\(\theta\) 。

非参数学习算法（Non-parametric learning algorithm）

      定义：一个参数数量会随m（训练集大小）增长的算法。通常定义为参数数量随m线性增长。换句话说，就是算法所需要的东西会随着训练集合线性增长，算法的维持是基于整个训练集合的，即使是在学习以后。

局部加权线性回归算法，是一种非参数学习法（non-parametric）

算法思想：

    假设对于一个确定的查询点\(x\)，在\(x\)处对你的假设\(h(x)\)求值。

    对于线性回归，步骤如下：

    1) 拟合出\(\theta\)，使 \(\sum_i(y^{(i)}-\theta^Tx^{(i)})^2\)最小

    2) 返回\(\theta^Tx\)

对于局部加权回归，当要处理\(x\)时：

     1) 检查数据集合，并且只考虑位于\(x\)周围的固定区域内的数据点

     2) 对这个区域内的点做线性回归，拟合出一条直线

     3) 根据这条拟合直线对\(x\)的输出，作为算法返回的结果

用数学语言描述即：

    1) 拟合出\(\theta\)，使 \(\sum_iw^{(i)}(y^{(i)}-\theta^Tx^{(i)})^2\)最小

    2) \(w\)为权值，有很多可能的选择，比如：

\[w^{(i)}=exp\bigg(-\frac{(x^{(i)}-x)^2}{2\tau^2}\bigg)\]

- 其意义在于，所选取的\(x^{(i)}\)越接近\(x\)，相应的\(w^{(i)}\)越接近1；\(x^{(i)}\)越远离\(x\)，\(w^{(i)}\)越接近0。直观的说，就是离得近的点权值大，离得远的点权值小。

- 这个衰减函数比较具有普遍意义，虽然它的曲线是钟形的，但不是高斯分布。\(\tau\)被称作波长，它控制了权值随距离下降的速率。它越小，钟形越窄，\(w\)衰减的很快；它越大，衰减的就越慢。

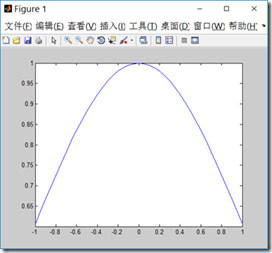
下图就是\(x\)在(-1,1)之间，\(\tau\)为1的衰减函数图：

x=-1:0.05:1;

y=exp(-x.*x/(2*1^2));

plot(x,y);

这样对局部加权线性回归，它的损失函数为：

\[J(\theta)=\sum\limits_{i=1}^{m}w^{(i)}\big[y^{(i)}-\theta^Tx^{(i)}\big]^2\]

\[w^{(i)}=exp\bigg(-\frac{(x^{(i)}-x)^2}{2\tau^2}\bigg)\]

     算法思路：假设预测点取样本点中的第\(i\)个样本点（共\(m\)个样本点），遍历1到\(m\)个样本点（含第\(i\)个），算出每一个样本点与预测点的距离，也就可以计算出每个样本贡献误差的权值，可以看出\(w\)是一个有\(m\)个元素的向量（写成对角阵形式），代入上式\(J(\theta)\)中。

\[w=\begin{bmatrix}
  w_1& &  &  & \\
  &  \ddots& &  & \\
  &  & w_i & & \\
  &  &  & \ddots & \\
  &  &  &  & w_m
\end{bmatrix}\]

\[J(\theta)=\sum\limits_{i=1}^{m}w^{(i)}\big[y^{(i)}-\theta^Tx^{(i)}\big]^2=y^Twy-\theta^Tx^Twy-y^Tw^Tx\theta+\theta^Tx^Twx\theta\]

利用最小二乘法，可以计算出一个\(\theta\)向量（一个预测点对应一个向量）,矩阵求导公式可以参考：http://www.cnblogs.com/mikewolf2002/p/7588126.html

\[\bigtriangledown_{\theta}J(\theta)=0 \\ -x^Twy-x^Twy+2x^Twx\theta=0 \\ \theta=(x^Twx)^{-1}x^Twy\]

3) 返回\(\theta^Tx\)

总结：对于局部加权回归，每进行一次预测，都要重新拟合一条曲线。但如果沿着x轴对每个点都进行同样的操作，你会得到对于这个数据集的局部加权回归预测结果，追踪到一条非线性曲线。

*局部加权回归的问题：

由于每次进行预测都要根据训练集拟合曲线，若训练集太大，每次进行预测的用到的训练集就会变得很大。

下面是局部加权线性回顾matlib代码，数据文件下载：https://github.com/pbharrin/machinelearninginaction/tree/master/Ch08

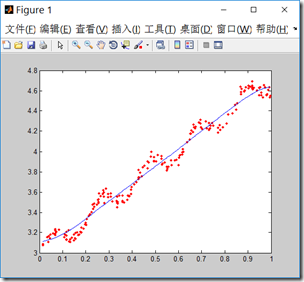
%局部加权线性回归算法（LWR/LOESS）  
clc;
clear all;
close all;
%%  
%载入数据  
data=load ('ex0.txt');
x=data(:,1:2);
y=data(:,3);
%%  
m=size(x,1);%样本数  
n=size(x,2);%特征维数  
tau=1;
w=zeros(m,m);
theta=zeros(n,m);%每一列都是一个样本的theta值  
for i=1:m
    for j=1:m
        w(j,j)=exp(-((x(i,2)-x(j,2))^2)/(2*tau^2));
    end
    theta(:,i)=((x'*w*x)\x')*w*y;  %左除式
end
figure;
plot(x(:,2),y,'r.');%原始数据  
hold on;
y_fit=x*theta;
y=diag(y_fit);%取对角线元素  
data(:,1:2)=x;
data(:,3)=y;
data=sortrows(data,2); %按第二列排序数据 
x=data(:,1:2);
y=data(:,3);
plot(x(:,2),y);

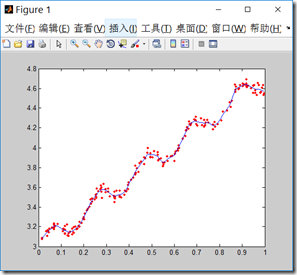
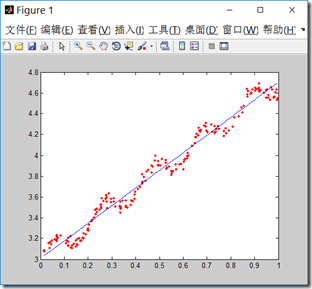
当波长\(\tau\)为1，这是回归曲线接近一条直线，随着波长减小，回归曲线更好的拟合样本数据，但要注意过拟合的问题，选择合适的波长值。

\(\tau=1\)

\(\tau=0.1\)

\(\tau=0.01\)